回溯法—图着色问题

最新推荐文章于 2025-04-14 22:46:41 发布

A snicker

最新推荐文章于 2025-04-14 22:46:41 发布

阅读量2.3k

点赞数 1

分类专栏：算法文章标签：数据结构算法

本文链接：https://blog.youkuaiyun.com/nice___amusin/article/details/117600848

版权

算法专栏收录该内容

19 篇文章

订阅专栏

该博客讨论了无向连通图的图着色问题，目标是找到最小的整数m，使得所有顶点使用m种颜色进行着色，且相邻顶点颜色不同。提供的代码实现了图着色算法，通过不断尝试和回溯找到解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

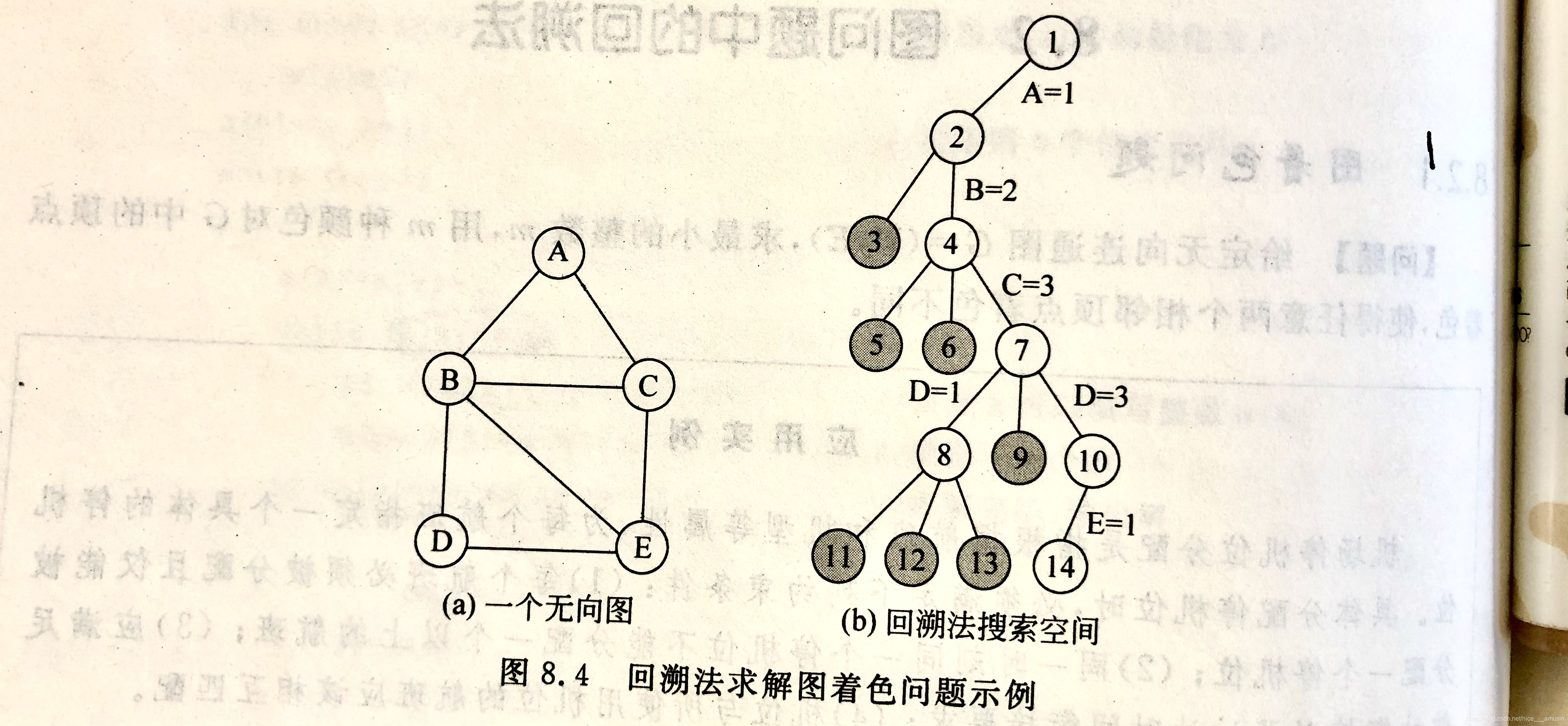
图着色问题描述为：给定无向连通图G=(V, E)和正整数m，求最小的整数m，使得用m种颜色对G中的顶点着色，使得任意两个相邻顶点着色不同。
在这里插入图片描述

代码：

int n;
int color[1000];	//n个顶点的着色情况
int arc[1000][1000];	//存储顶点之间边的情况

int Ok(int k) {							//判断顶点k的着色是否发生冲突
	for (int i = 0; i < k; i++) {
		if (arc[k][i] == 1 && color[i] == color[k]) {
			return 0;
		}
	}
	return 1;
}

void GraphColor(int m) {	//m个颜色
	int i, k;
	for (i = 0; i < n; i++) {
		color[i] = 0;			//数组color初始化为0
	}
	k = 0;
	while (k >= 0) {
		color[k] = color[k] + 1;	//取下一个颜色

		while (color[k] <= m) {
			if (Ok(k)) {			//不冲突
				break;
			}
			else {
				color[k] = color[k] + 1;	//搜索下一个颜色
			}
		}

		if (color[k] <= m && k == n - 1) {	//求解完毕后，输出解,顶点全部着色
			for (i = 0; i < n; i++) {
				cout << color[i] << " ";
			}
			return;
		}

		if (color[k] <= m && k < n - 1) {	//顶点k是一个合法着色
			k = k + 1;					//处理下一个顶点
		}

		else {
			color[k--] = 0;				//回溯
		}
	}
}