基于SOM的医疗可达性预测

基于自组织映射的医疗基础设施可达性需求预测洞察

摘要

随着全球城市人口的增长，对可及性——居民到达重要场所或机会的便利程度——进行深入分析变得愈发重要。大数据与机器学习（ML）等计算技术的进步相结合，可能为城市可及性研究带来重大机遇，但其在该领域的应用仍较为有限。本研究结合经典与现代数据分析方法，对一个快速发展的城市中医疗设施的可及性进行了详细预测，并探讨了其与社会经济因素的关系。以加拿大素里市为案例研究，我们利用主成分分析（PCA）和一种强大的机器学习聚类工具——自组织映射（SOM），对2016年和2022年的高分辨率收入数据进行了聚类分析。随后，我们将这些结果与通过简单开源工具计算得出的前往医院和诊所的门到门出行时间相结合。在分析中重点关注老年人口（65+岁及以上），我们发现，在研究期间内，萨里的高收入群体预计将进一步扩大。无论是在2016年还是2022年，低收入群体平均而言比高收入群体享有更好的医疗设施可及性。对于现有医疗可及性较好的社区，人口增长将成为最大的可及性挑战；而在连接性差的社区，收入变化（无论是上升还是下降）将带来最严峻的挑战。萨里可能出现双重可及性问题：第一，大量老年人口将居住在拥有众多且邻近诊所的区域，这将给提供专科服务的现有设施带来压力；第二，低收入老年人将越来越多地居住在与医疗服务连接性差的地区，可能影响医疗可及性的公平。我们证明，结合主成分分析（PCA）和自组织映射（SOM）聚类技术，能够为预测社区层面的可及性提供新颖的见解，从而从大规模多变量数据集中得出可靠的规划政策建议。

关键词 ：智慧城市；机器学习；大数据；聚类；主成分分析（PCA）

1. 引言

可及性（人们到达地点或获取机会的难易程度）是衡量城市宜居性和可持续性的重要指标。在全球推动城市“智慧化”的进程中，城市互联互通的趋势日益明显，尤其体现在对物理基础设施和信息通信技术（ICT）[1,2]的投资上。由互联设备和传感器组成的创新网络，结合智能应用和数据分析，彻底改变了从城市政府到市民等各类主体同时优化现有系统[3]、提升城市居民生活质量[4,5]、满足可持续发展需求[6–8]的方式。目前普遍呼吁智慧城市建设应确保其服务在增长的同时保持包容性和公平性[9,10]，因为证据表明，基本服务的普遍获取对人类发展和社会进步有积极影响[11–14]。

然而，在不同发展阶段的城市中，居民对基本服务的获取仍存在差距。因此，可及性通常通过公平这一视角进行研究，公平可被定义为为个人享受健康而充实的生活提供机会[15]。在许多国家，医疗保健获取是一项基本权利[16]，因为它在满足人们诸多基本需求方面发挥着关键作用。医疗可及性方面的差距源于多种物理和社会经济因素，包括社会地位、家庭收入、交通基础设施以及城市空间分布[17,18]，但在复杂的城市结构中明确界定因果关系十分困难[19]。医疗可达性差已知会导致医疗保健利用率降低和健康结果不佳[18,20,21]，因此确定新建医疗设施的位置一直是城市规划者面临的持续挑战。此外，生育率下降和寿命延长正导致年长、移动性较低的人口增加，其可及性需求与年轻、移动性更强的人群不同[15,22]。对于不断发展的城市而言，一个主要问题在于确保其交通系统在不同人口群体之间保持包容性和公平性[23]。

先前的研究试图在不同尺度上将城市可及性模式与人口统计和社会经济因素联系起来。这些研究范围从全球范围内对城市中心的可及性[24]，到特大城市尺度上的体育基础设施可及性[25]，再到社区尺度上对基本服务的可及性[26]。这些研究中的常见方法是推导出服务区域人口基本特征之间的统计关系。然而，尽管此类分析能够提供有价值的见解，但中位数或分组收入等基本描述符并不总能为跨人群的可及性变化提供足够的细微差别以支持深入分析。

城市领域中“大数据”的日益普及使得在越来越精细的尺度上观察、分析和预测人类行为成为可能[27–29]。基于机器学习（ML）技术的计算数据挖掘的进步也使研究人员能够更好地理解这些丰富数据集[30]。当此类方法为“无监督”时，意味着无需对模式具备先验知识[31]。能够以这种方式自我学习的算法适用于处理未经分类的数据，包括需要从观测数据中估计潜在概率密度函数的情况[30]。

一种强大的无监督机器学习算法是自组织映射（SOM），它利用人工神经网络来表征数据集中的变异性并总结关键特征[32]。SOM算法已应用于广泛的学科领域（参见参考文献[33]中的综述），从火山地震谱[34]和大气气溶胶追踪[35]的分析到地价预测[36]。其他机器学习技术（例如，神经网络、随机森林分类器）也已应用于城市交通问题，包括预测交通流量[27]、出行方式选择[37]以及公共交通卡使用聚类[38]。然而，尽管SOM在直观可视化复杂社会人口统计模式方面具有潜力，尤其有助于政策制定[42,43]，但除了一些例外情况（例如，[39–42]），其在社会科学领域的应用影响相对有限。

本研究旨在探讨社会经济因素与经历快速人口增长的城市中可及性之间的关系。我们分析了2016–2022年间收入空间分布的变化可能对加拿大素里市医疗服务可及性产生的潜在影响。我们将萨里作为全球众多面临人口变化和城市发展挑战的现代富裕城市的代表性案例研究。我们的分析聚焦于老年人（65+岁及以上），因为他们比一般人群具有更复杂的医疗需求，因此在制定卫生与交通政策时需要特别关注[44]。在Mayaud等人[26]关于萨里医疗与学校服务范围研究的基础上，我们提出一种结合两种聚类方法的方法论，以探索收入在时空上的分布模式：（i）主成分分析（PCA）与层次聚类，以及（ii）自组织映射（SOM）。我们采用这两种方法来降低收入数据集的维度，并提取其中的分布模式基础数据，然后将其与可达性指标相关联。尽管主成分分析（PCA）和自组织映射（SOM）本身均为成熟的分析方法，但我们结合经典与现代数据分析方法，为城市在人口增长、收入分配以及基本服务可及性方面的演变提供了新颖且详细的见解。

本文其余部分分为三个部分。下一节介绍我们案例研究的社会经济背景，概述所使用的数据来源，并解释本研究中主成分分析（PCA）和自组织映射（SOM）的应用。第3节展示我们的分析结果并对结果进行讨论。第4节总结本文的主要结论。

2. 方法

2.1. 研究区域

素里市是大温哥华区域局23个地方当局之一，也是不列颠哥伦比亚省最大的城市之一，拥有52万名居民。自2000年以来，该市人口增长了~40%，预计到2041年人口将达到~800,000，使其成为该地区增长最快的城市[45]。过去二十年间，老年人比例从10%上升到14%，而儿童和青少年（0‐19岁）的比例在同一时期则从30%下降到24%[46]。

2.2. 数据来源

为了强调本研究中分析方法的可转移性，我们完全依赖开放数据源和开源代码。我们利用在最小标准人口普查地理层级——传播区（DA）[46]收集的加拿大人口普查数据，评估了萨里市的人口特征（人口数量、收入和年龄）。通过DemoStats数据库[47]获取了2016年的人口普查数据（目前可获得的最新完整普查数据集）以及2022年的预测数据（我们可获得的最新高分辨率预测数据）。这些2022年预测数据——应视为未来人口情景可能范围中的其中一种情况——由DemoStats基于计量经济学、人口统计学和地理模型的组合编制而成[48]。

DA级别的普查数据被重新组织成一个覆盖素里市边界的网格，该网格由1480个等大小六边形组成，每个六边形的对角直径为500米（0.16平方公里²）。选择六边形单元的形状是为了减少边缘效应带来的抽样偏差，而网格单元的大小设计旨在为我们的空间数据提供足够的细粒度，同时大致匹配萨里地区DA的平均面积。这有助于在将普查数据分配到六边形网格单元时最小化降尺度误差。我们采用了[26]的方法将普查数据分配到每个六边形网格单元（详见《补充材料》第1.1节的简要说明）。

医疗设施（门诊诊所和医院）的位置数据来自不列颠哥伦比亚省和萨里的开放数据目录。我们共获取了两家医院和33家门诊诊所的位置数据。《补充材料》第1.2节讨论了本研究中对医院和诊所的定义与选择方式。

使用开放街道地图（OSM）确定行人基础设施和道路网络的空间布局，这构成了门到门路径规划算法的基础，用于计算出行时间（见第2.6节）。OSM是志愿地理信息的一个典型例子，用户自愿参与其开源开发。因此，关于其在全球某些地区的准确性存在一些疑问。在对开放街道地图“完整性”的一项全球分析中，巴林顿‐利和米拉德‐鲍尔[49]发现加拿大的街道网络已完全覆盖，因此我们认为OSM在本文所呈现的分析中具有可靠的完整性。

从区域交通运营商跨链接获取了2017年9月的公共交通线路和站点的地理定位时刻表数据。这些数据以通用交通数据规范（GTFS）格式组织，反映了交通时刻表规划，但不包含动态交通拥堵信息。

2.3. 数据准备

我们旨在分析素里市收入分布与可达性指标之间的关系。类似于[50]，我们首先通过主成分分析（PCA）降低收入分布数据集的维度，该方法可识别出反映收入分布数据集最大变异性的特征。随后，我们将SOM算法应用于收入数据。

为了对分类人口普查数据执行主成分分析（PCA）和自组织映射（SOM）技术，我们首先使用帕累托收入分布定律估算收入分配中未定义的上限值（参见《补充信息》第1.3节）。对于2016年的所有数据区，最后一个开放‐ended收入类别的中点被计算为266,950美元。然后，我们通过为每个收入区间分配一个基本的中点估计值，并将每个估计值重复Z次以形成向量，从而将分类数据转换为连续的数据分布，其中Z是该区间出现的频率[51]。我们使用MATLAB内置的“ksdensity”核平滑方法进行核密度估计（KDE），这是一种广泛使用的概率密度函数估计技术[52–55]。每个收入向量的核密度估计结果通过减去均值并除以其标准差进行去均值和标准化处理。这为我们提供了每个网格单元内收入的平滑且标准化的连续概率分布，作为主成分分析（PCA）和自组织映射（SOM）算法的输入。

2.4. 主成分分析和层次聚类

主成分分析（PCA）是一种经典的数据分析方法，用于降低高维数据集的维度。根据[34]，我们采用[56]中关于PCA概念的术语命名方式。在主成分分析（PCA）中，一个高维数据集被分解为一组线性无关‘模态’（也称为‘特征向量’）。这些模态是张成原始数据集空间的基函数，并被选择以使每个模态所解释的方差最大化[57]。原始数据集可以通过将每个模态乘以一个“主成分”（PC）后求和来重建；换句话说，主成分（PC）是数据在各模态上的投影数据：
$$ d_i = \sum_{j=1}^{N} PC_{ij} \cdot e_j $$
其中$ d_i $是数据集，$ e_j $是模式，$ PC_{ij} $是主成分，N是模式的总数。或者，可以仅使用前几个（最重要的）模式来重构原始数据集，从而在过滤噪声的同时保留大部分方差：
$$ d_i = \sum_{j=1}^{M} PC_{ij} \cdot e_j $$
其中M是所选模式的数量，满足M << N。

为了比较2016年至2022年期间典型收入分布在空间上的变化，我们首先对2016年收入分布数据集进行主成分分析（PCA）。这将数据集分解为模式和主成分，有助于捕捉数据集中变异性最大的位置。

接下来，我们在前三个主成分的空间中使用层次聚类方法对2016年每个KDE进行聚类。我们仅使用前三个模式，因为它们包含了>97%的2016年数据集的方差（即，我们根据收入分布被前三个模式重建的相似程度进行分组；参见第3.1节）。使用树状图来确定最优聚类数量[58]。通过各聚类成员的平均主成分构建典型聚类模式。最后，我们计算每个2022年收入KDE与每个2016年聚类模式之间的均方根误差（RMSE），并将每个2022年KDE分配给产生最小RMSE的聚类。通过这种方式，我们根据2022年收入分布与观察到的2016年聚类模式的相似性对其进行分组，并以RMSE作为相似性度量指标。

本研究中，使用主成分分析（PCA）来确定自组织映射（SOM）聚类输出的真实性。我们承认使用预设的聚类算法与无监督的SOM进行比较具有一定的定性性质。一些研究试图更可靠地识别最优聚类数量，使得对应的重构光谱彼此之间差异最大[34]，但此类附加方法超出了本研究的范围。k均值是另一种传统聚类算法，已被应用于城市科学领域的研究中[59–61]。我们在前三个主成分的空间中执行k均值聚类，并与层次聚类的结果进行比较，结果如图S5所示。我们发现这两种方法产生了相似（如果不是完全相同）的结果；由于我们的目标是将传统聚类算法与自组织映射进行比较，因此我们选择采用层次聚类来开展后续分析。

2.5. 自组织映射

SOM方法与PCA类似，两者都用于将多维数据集（即所有人口普查分区（DAs）的收入分布）的维度降低为一组较少的特征模式（即特征性收入分布）。主成分分析（PCA）将数据分解为一组线性无关模式，以捕获最大方差，而自组织映射（SOM）方法则将输入数据空间进行非线性投影，映射到二维网格或“地图”上的一组单元（神经网络节点）。关于SOM算法的详细描述和应用，我们建议读者参考[32,34,56,62]。此处，我们讨论SOM相较于主成分分析（PCA）的主要特点。

SOM方法识别出的典型收入分配模式类似于前一节讨论的收入分配的PCA模式。在PCA中，空间信息包含在主成分（PCs）中（即PCs描述了给定模式在某个分区收入分配中的出现强度），而在二维SOM中，空间信息则编码于其位置上。SOM通过一个迭代的“训练”过程创建，其中每个分区被投影到SOM中的一个非唯一位置，而SOM中的每个位置都关联着一种典型的收入分配。一个分区所映射到的节点称为“最佳匹配单元”（BMU）。该BMU的谱以及其邻近节点的谱随后会被调整，以更接近输入样本。算法的学习特性使得网络在训练阶段不断演化。SOM方法的一个关键特征是，在二维图上某个节点的模式会比距离较远的节点更接近其邻近节点的模式，这一点是PCA无法体现的。因此，位于图对角角落的模式往往彼此差异最大。

与主成分分析（PCA）类似，我们关注的是特征收入分布在空间上的出现情况如何随时间变化。我们首先使用2016年收入分布创建一个自组织映射（SOM），从而得到：（i）被分配到二维地图上各节点的特征收入分布；以及（ii）一张城市地图，其中2016年的每个分区（DA）都被分配了一个最佳匹配单元（BMU）。接下来，我们通过计算每个2022年收入分布与SOM中每个特征收入分布之间的均方根误差（RMSE），将2022年每个DA的收入分布分配到2016年SOM的某个节点上。对于该DA在2022年的分配，具有最低RMSE的节点即为其最佳匹配单元（BMU）。

本研究中使用的SOM算法改编自[62]开发的代码。简而言之，我们使用开源的基于MATLAB的SOM工具箱[63,64]创建一个大型自组织映射（SOM）。然后对这个大型SOM中的模式进行主成分分析（PCA），并为每个节点定义“拓扑结构”，即前两个主成分平方和。我们将模式的数量确定为该拓扑结构中局部极大值和全局最小值的数量。局部极大值代表数据集中方差最大的模式，而全局最小值代表最不能由前两个模态描述的模式，因此与局部极大值差异最大。最后，我们根据此节点数量创建一个较小的SOM，并使其形状的宽高比尽可能接近大型SOM。我们通过设定不同大小的SOM来测试结果的敏感性，但仅展示8聚类（4行 × 2列）地图的结果（见第3.2节）。

2.6. 可达性分析

流域区分析为估算在给定出行时间阈值内能够从家中到达医疗设施的人口构成提供了基础。我们的方法的详细描述见参考文献[26]，并在补充信息第1.4节中进行了总结。简而言之，我们使用开源路由引擎OpenTripPlanner[65]通过最优结合步行和公共交通，计算每一对“起点”和“终点”（O‐D）网格单元之间的出行时间估计值。我们应用了一种改进的等时线法或累积机会法[25,66]来估算理论上可在30分钟时间阈值内获得医疗设施服务的居民数量。可接受的出行时间因交通方式以及社会人口统计和生活方式因素而异，因此我们选择30分钟作为阈值，因为大多数大都市交通规划均采用该标准来评估通过公共交通实现的可及性[67]。此方法的局限性在补充信息第1.4节中有更详细的探讨。

在这一项纵向研究中，我们对2016年和2022年采用了相同的分析方法。换句话说，我们假设在研究期间设施分布和交通时刻表保持不变；仅根据预测数据调整了人口和收入数据。我们承认，随着未来投资的增加，服务供给可能会发生变化，但由于缺乏有关规划中的基础设施和时刻表变更的可靠数据，我们假设2022年的交通网络和医疗服务供给保持不变。相反，通过单独分析人口和社会经济变化对医疗服务覆盖区域规模和构成的影响，我们的分析可作为服务需求的基线研究，为今后关于服务供给和交通能力变化的研究提供参考。

3. 结果与讨论

3.1. 主成分分析的洞察

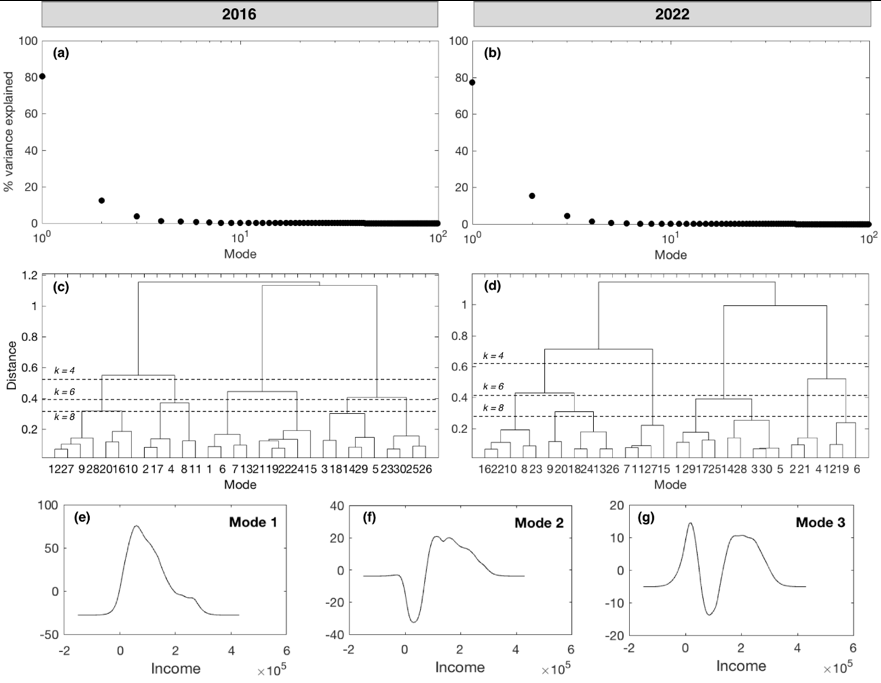
本研究中，我们使用主成分分析（PCA）和层次聚类来确定在自组织映射（SOM）中应设定的最优聚类模式数量。如第2.4节所述，我们将每个网格单元中收入的去均值化、归一化的连续概率分布作为主成分分析的输入。各模式解释的总方差比例（图1a,b）显示，前三个模式共同解释了>97%的方差，在2016年和2022年收入数据中均是如此。考虑到收入分布通常具有相对普遍的对数正态或威布尔分布形状[51]，我们的主成分分析第一个模式能够捕捉如此高的方差（~80%）并不令人意外。其余由前三个模式之外的模式所解释的方差可能主要归因于噪声的影响。

每个单元格中收入的核密度估计（KDE）是图1e–g所示模式的线性组合。第一种模式是向低收入倾斜的接近正态分布（图1e），第二种模式（取决于其符号）将分布加权至较低或较高的收入（图1f），第三种模式（取决于其符号）则拓宽或收窄核密度估计（图1g）。2016年数据集三个主模式对应的主成分的空间分布在补充信息中的图S1中展示。这些地图显著突出了城市西北部和东南部模式2存在负主成分，意味着相较于南部和东北部，该区域低收入家庭更普遍。

图1c、d中的树状图表明，对于2016年和2022年的数据集而言，当聚类数量为k= 4–8时，在减少聚类数量与保持相对较低的簇内方差之间达到了较好的平衡。当聚类数量为k= 8时，其空间映射的PCA聚类拓扑如图2a, b所示，代表性聚类模式见图2c。到2022年，聚类5和聚类6在城市范围内扩散，而聚类1有所减少。这些变化反映在各聚类所对应的人口比例中（图2d）。各聚类的中位年龄在研究期间显示出一定变化，尤其是聚类5–8，其中位年龄增加了至少4年（图1e）。聚类5–8主要出现在农村社区，这表明老年人口可能正在向城市基础设施普遍较差的地区增加。

2016年和(b)2022年。主成分模式（PCs）和主成分（PCs）使用2016年数据集计算得出，并将2022年数据投影到2016年的模式上以获得2022年的主成分。白色单元格表示无数据；(c)每个PCA聚类最具代表性的频率分布，加粗部分显示其在2016年和2022年地图中的出现频率。这些图表的y轴围绕零值变化，因为输入数据已通过减去均值并除以其标准差进行去均值和标准化处理；(d)属于每个聚类的城市总人口比例，对应2016年和2022年；(e)属于每个聚类的人口中位年龄，对应2016年和2022年。)

3.2. 自组织映射

3.2.1. 将自组织映射（SOM）拓扑与可及性和出行时间关联起来

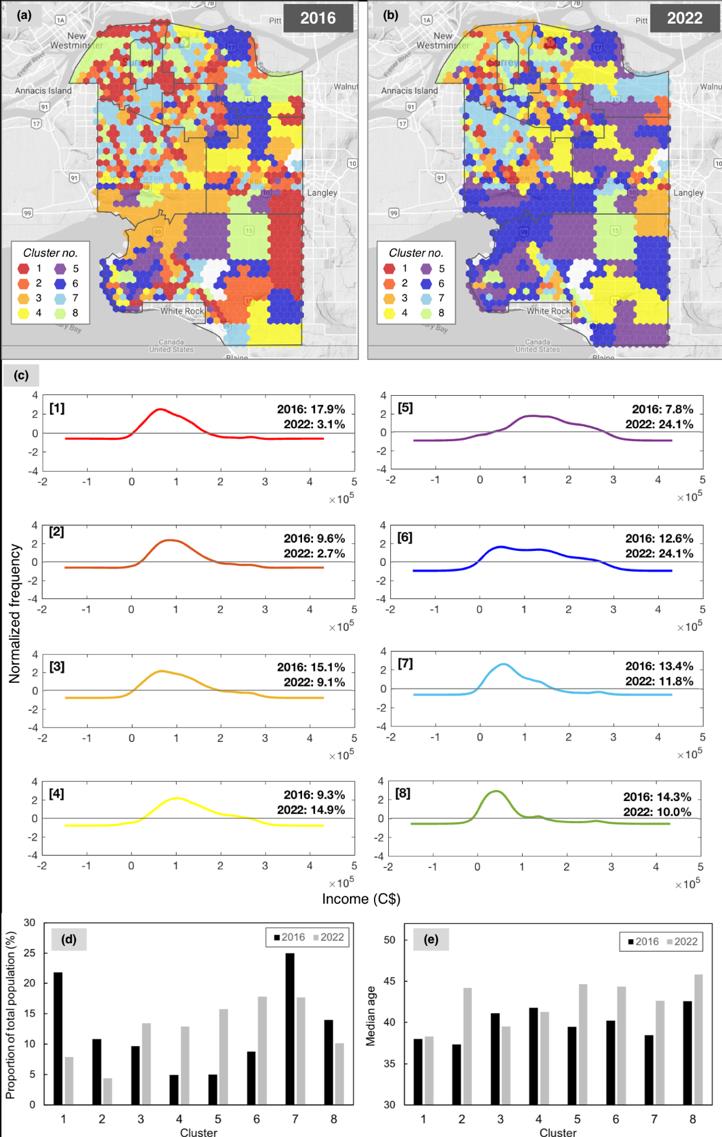
基于主成分分析（PCA）的结果，8个聚类（k= 8）在保持相对较低的簇内方差的同时提供了良好的模式多样性，因此我们训练了一个用户定义为4行 × 2列的自组织映射（SOM）。2016年和2022年收入数据的空间映射SOM拓扑结构以及特征频率分布如补充信息中的图S2所示。虽然分别考察八个聚类的分布是有用的，但SOM的优势在于它在二维地图中提供了聚类之间的相对结构。由于SOM在垂直方向上被拉伸，地图的顶部和底部模式之间存在一种对偶性：第1和第5聚类模式最为相似，第4和第8聚类模式也是如此。我们并不选择详细地独立考虑这八个聚类，而是将其中一些聚类进行组合以简化分析。由于第1和第5聚类的特征是接近正态的收入分布，我们将它们归为“高收入”类别（图S2）。相反，第4和第8聚类具有更明显的正偏分布，表明低收入的贡献更大，因此我们将它们归为“低收入”类别。在分组分析中，我们不考虑第2、第3、第6和第7聚类。这种方法有助于突出收入模式方面最显著的差异。

分组聚类的空间映射SOM拓扑结构如图3a,b所示。2016年，该城市27%的网格单元为高收入群体，18%为低收入群体，其中低收入群体集中在西北部的市中心。居住在高收入（18%）和低收入（16%）区域的总人口比例相似（见图3c）。到2022年，高收入群体的覆盖范围显著增加，有时会扩展至先前的低收入区域。这一发现对于使用2016年数据或2022年数据训练的SOM均具有稳健性（参见补充信息中的图S3）。正如萨里人口老龄化趋势所预期的那样，到2022年所有聚类的中位年龄都将上升（图S2e），尽管低收入群体的老龄化程度平均高于高收入群体（见图3d）。

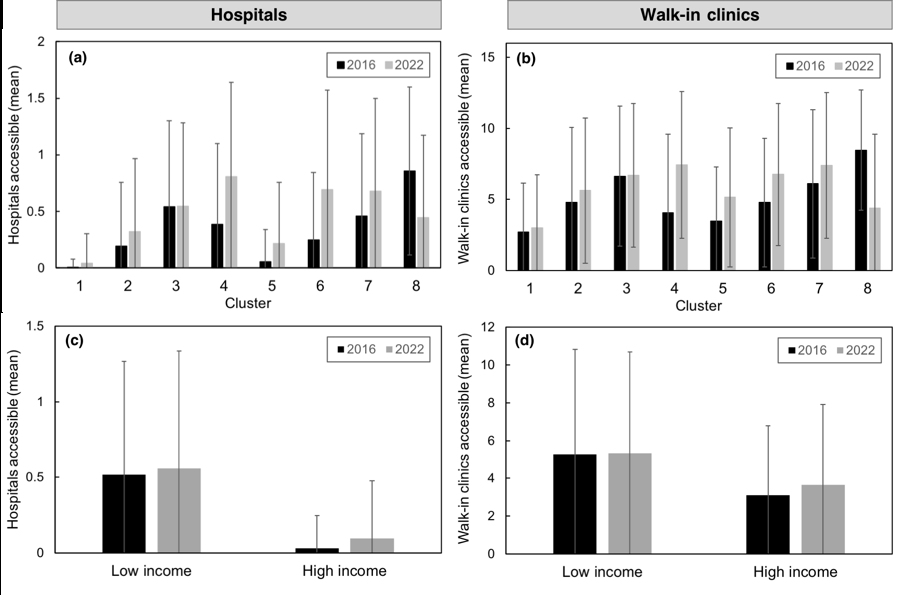
SOM聚类提供了一种对每个网格单元计算出的可达性指标进行分组的方法，从而可以确定每个聚类对医疗设施的综合可达性（见图4）。尽管可达性水平存在一定的显著变异性，但在研究期间，大多数聚类的居民能够到达的医院平均数量（图4a）和门诊诊所平均数量（图4b）均有所上升。这种情况的发生是因为许多原本位于更偏远、连接性差的聚类成员在2022年转变为聚类1或第8聚类，从而提高了剩余成员的平均可达性（例如，同时降低了第8聚类的可达性）。分组后，低收入群体对医院的平均可达性（图4c）和门诊诊所的平均可达性（图4d）明显优于高收入群体。2016年至2022年间，低收入和高收入群体的可达性均有所提高（对于低收入群体而言，聚类4的可达性增加弥补了第8聚类可达性下降的影响）。具体的聚类间转移将在第3.2.4节中进一步详细探讨。

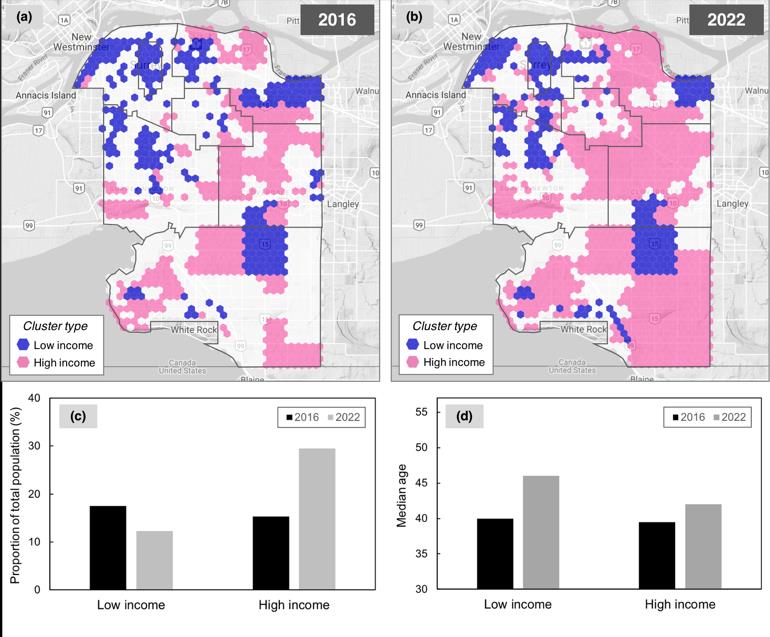
SOM聚类转换和人口结构变化将对老年人的可及性产生不同的影响。到2022年，多出~12,000名老年人将居住在无法到达医院的区域（图5a），多出~1500名老年人将居住在无法到达门诊诊所的区域（图5b）——在这两种情况下，大多数人将来自高收入聚类1区域。居住在可及性为零家医院的高收入群体中老年人数量将大幅增加（图5c）。与此同时，超过15,000名老年人将能够到达至少一家门诊诊所，其中大多数居住在高收入社区（图5d）。由于需求将集中在少数几家服务于老年人口较多社区的诊所，这可能会给现有诊所提供特定医疗服务带来压力。

3.2.2. 随时间变化差异的归因

我们现在考察随时间推移的可及性变化主要是由每种聚类模式出现频率的变化引起，还是由每种聚类模式内部的人口变化引起。为此，我们采用[62,68]提出的方法，该方法使用交叉项分析来检测当前和未来气候现象之间差异的来源。在本研究中，2016年和2022年的八种聚类模式中的每一种都对应着能够获得特定数量设施的人口。对于基准年（即2016年），城市中所有聚类内能够获得特定数量设施的总人口（T）（P T,2016）可表示为：
$$ P_{T,2016} = \sum_{n=1}^{N} f_n p_n $$
其中N是自组织映射（SOM）中的模式总数（即N= 8）；$ f_n $为居住在每个聚类中的人口比例；而$ p_n $为可及特定数量设施的一般人群的平均人口。

每个属于该聚类的网格单元。为了评估2016年和2022年之间差异来源的量级，PT在2022年（PT, 2022）可以表示为2016年的PT,2016加上PT的变化量，即：
$$ P_{T,2022} = \sum_{n=1}^{N}(f_n + \Delta f_n)(p_n + \Delta p_n) $$
其中 $ \Delta f_n = (f_{n,2022} - f_{n,2016}) $ 和 $ \Delta p_n = (p_{n,2022} - p_{n,2016}) $。方程(4)可展开为：
$$ P_{T,2022} = \sum_{n=1}^{N} f_n p_n + f_n \Delta p_n + \Delta f_n p_n + \Delta f_n \Delta p_n $$
在方程(4)中，第一项差值项（$ f_n \Delta p_n $）是模式内变异性分量，反映了具有特定收入水平（即聚类成员身份）的人口进入或离开城市的情况。例如，正值的模式内变异性分量（$ f_n \Delta p_n > 0 $）可能表示2022年迁入城市的居民其收入分布（即聚类成员身份）与2016年相似。第二项差值项（$ \Delta f_n p_n $）是模式频率分量，反映了具有特定收入水平的人口在城市中的分布变化，这种变化可能是由于城市内部人口流动或个人随时间变得 richer/poorer 所致。例如，负的模式频率分量（$ \Delta f_n p_n < 0 $）表明，平均每聚类人口相同的情况下，经历总人口比例下降的聚类数量多于经历上升的聚类数量。第三项差值项（$ \Delta f_n \Delta p_n $）是综合项。

我们对医院和门诊诊所进行了这种差异归因分析。在这两种情况下，分析分别针对可及零个设施的人群（P0）和可及一个或多个设施的人群（P≥1），并分别针对城市老年人口和总人口（所有年龄段合计）进行（表1）。对于这两类人群，当居民可及一个或多个医疗设施时（P≥1），模式内变异性分量（$ f_n \Delta p_n $）是最大的差异项。该变异性分量多为负值，意味着整体而言，到2022年，迁入城市的居民与2016年相比将具有不同的收入分布（例如，高收入个体将迁入此前为低收入的社区）。相反，当零个设施可及时（P0），对于老年人口和总人口而言，模式频率分量（$ \Delta f_n p_n $）是最大的差异项。该分量的正值可能反映出人们在城市内部重新分布至不同社区，或经历了收入变化（例如，老年人退休后收入下降）。

情景	Net 差异	模式内变异性 组件（fn ∆pn）	模式频率 组件 (∆fnpn)	合并 Term
医院
可及性 = 0
老年人	11,775	5317	6031	426
总人口	27,575	−16,454	47,389	−3359
可及性 > 0
老年人	5595	11,710	−5650	−464
总人口	16,495	56,801	−44,311	4005
随到随诊 诊所
可及性 = 0
老年人	1429	−110	1392	148
总人口	2620	−6091	10,277	−1565
可及性 > 0
老年人	15,941	17,137	−1011	−186
总人口	41,450	46,438	−7199	2211

这些结果表明，在目前没有医院/门诊诊所可及性的地区，由居民（再）分布或居民贫困化或富裕化所导致的可及性变化将超过因人口进出城市所带来的变化。相反的情况则适用于其他地区。

对于至少有一个医疗设施可及的区域而言，从政策和交通规划的角度来看，这意味着市政当局可能需要通过差异化的视角来考虑医疗可及性公平：在已有医疗可及性的社区中，人口增长可能会导致服务瓶颈，因此可能需要增加设施供给。而在连接性差的社区，应对收入变化（无论是正面还是负面）的影响可能需要调整公共交通基础设施和时刻表安排。这一点在老年人口增长预期最高的地区尤为重要，因为在这些地区私家车使用量可能会显著下降。

3.2.3. 最近设施的可达性

量化居民到达最近设施的快慢是可及性的一个补充度量。分组聚类到最近医院和门诊诊所的出行时间累积频率分布在图6中展示（所有聚类的单独分布见补充信息中的图S4）。高收入群体到医院（图6a）和门诊诊所（图6b）的出行时间明显长于低收入群体。从2016年到2022年，低收入和高收入群体到最近设施的出行时间均有所减少（即图表中的向左移动）。向更低累积出行时间的转变意味着设施对居民的平均可及性将提高，从而增加特定医疗地点服务的压力。与此同时，可能需要新增公交线路或更频繁的时刻表安排，以服务迁入城市更偏远农村地区的人群（例如，图S4f显示，到2022年，第8聚类（低收入）前往诊所的出行时间将显著延长）。

医院和(b)随到随诊诊所的出行时间累积频率分布，按低 （第4和第8聚类）和高（第1和第5聚类）收入分组。)

3.2.4. 聚类变化

绘制不同聚类之间的变化路径，揭示了最佳匹配单元成员资格随时间推移的演变情况（图7）。到2022年，聚类1占据主导地位，主要原因有两个：首先，最初属于聚类1的单元中有99%仍保留在聚类1中；其次，聚类1吸收了来自聚类2和聚类5的大量单元。到2022年，聚类6和聚类7的成员资格显著下降，原因是这些聚类中的单元转向了聚类2和聚类5。除从聚类7到聚类5外，未观察到跨越一个以上相邻模式的转换，这表明社区的收入分配预计不会发生剧烈变化。值得注意的是，没有任何聚类行呈现“向下移动”的趋势——换句话说，在整个城市范围内，未观察到从高收入向低收入的显著转变。我们的聚类图得益于自组织映射（SOM）的拓扑特性而更易于解释：由于在SOM上距离较近的聚类比距离较远的聚类更为相似，因此聚类“向上移动”的趋势表明萨里地区的收入水平呈现出从低到高的特征性变化。

该可视化突显了使用自组织映射作为向非专业人士（如政策制定者）传达随时间变化情况的工具的优势。

我们进行了“聚类距离”分析，以量化各个网格单元在2016年和2022年之间BMU成员资格的变化程度。为了计算聚类距离，我们首先对图S2中所示的八个基本制图单元的分布进行主成分分析（PCA），并选取前两个模态（解释了总方差的93%）及其对应的主成分用于分析。如果某个网格单元在2016年和2022年之间发生了BMU变化，则将该变化的幅度量化为PC空间中2016年聚类模式（PC1 2016, PC2 2016）与2022年聚类模式（PC1 2022, PC2 2022）之间的欧氏距离。对于在研究期间BMU未发生变化的网格单元，其聚类距离设为零。

不同医院和门诊诊所可及性水平的单元的中位聚类距离以箱线图形式显示在图8a,b中。尽管所有情况下的四分位距相对较大，但对医院可及性最差（即0）和最好（即2）的单元，其中位聚类距离最低（图8a）。相比之下，对门诊诊所可及性处于中等水平（即1–15）的单元，其中位聚类距离最低（图8b）。这支持了以下观点：收入分布变化最显著的地区将是目前对诊所可及性非常好或非常差的地区。

聚类距离的箱线图，按可及性水平分组，分别针对(a)医院和(b)门诊诊所；(c–f)散点图显示每个单元格中医疗设施可及性与欧几里得聚类距离之间的关系，第三个（彩色）变量显示2016年和2022年之间中位年龄的差异。)

为了进一步从人口统计学角度探讨这一现象，我们在图8c–f中展示了医疗设施可及性、欧几里得聚类距离以及2016年和2022年中位年龄差异之间的关系。中位年龄差异被用作老龄化的一个指示性指标；中位年龄的增加可能是由于老年居民流入所致，也可能是年轻人比例下降的结果，这在过去二十年萨里的整体趋势中已有观察到[46]。对于医院（图8c）和门诊诊所（图8d），中位年龄增长最大的（即颜色更红）的地区预计出现在医疗设施可及性较少且聚类距离较低的区域。这意味着老龄化人口将集中在医院和诊所可及性相对较差的地区，尽管这些地区的收入分布将保持相对稳定。相反，在经历较大收入分布变化和/或拥有大量医疗设施可及性的地区，中位年龄将下降（颜色更蓝）。从到最近设施的出行时间关系中也可得出相似的图景（图8e,f），老龄化最严重的群体位于离最近医院和诊所最远的地区，且这些地区的收入分布变化较小。正在较年轻的人群似乎主导了出行时间较短的相对稳定聚类，或出行时间较长（特别是前往医院）的不稳定聚类。

这些发现可能对萨里等城市中心的医疗可及性公平产生重要影响。到2022年，预计有超过15,000名老年人迁入至少拥有一家门诊诊所的地区，以及~3,000名老年人迁入可同时进入萨里两家医院的地区。人口老龄化速度最快的社区往往是医疗可及性较差的地区，其中许多为低收入社区。这可能导致老年人口面临双重可及性问题：首先，随着大量老年人迁入特定设施的服务范围，某些专科服务的现有设施可能面临更大压力；其次，低收入老年人将越来越多地居住在与医疗服务连接性差的地区，尤其是农村郊区。

4. 结论

强大的机器学习（ML）技术是稳健分析日益庞大的城市数据集的重要工具。正如本研究所示，自组织映射（SOMs）等机器学习方法为揭示潜在数据模式提供了可靠途径，并可利用大型多变量数据集推荐可行的政策干预措施。我们使用自组织映射（SOM）对素里市的收入分布进行表征，绘制其在时空上的变化情况，并将其与医疗服务的可及性指标关联起来。通过与主成分分析（PCA）和层次聚类相结合的方法输出结果进行比较，以确定最终地图所需的最优聚类数量。

我们的研究结果表明，像萨里这样快速变化的城市中心可能很快会面临双重可及性问题。首先，大量老年人口将迁入诊所可及性很高的地区，从而给现有设施带来压力。其次，低收入老年人将越来越多地居住在与医疗服务连接性差的地区。这些动态引发了关于交通方式选择的重要问题，因为高收入老年人可能通过拥有和使用私家车，在一定程度上缓解医疗可及性低的影响，而低收入老年居民则可能高度依赖公共交通。我们的分析未包含私家车，因此未来的研究应整合交通方式选择，以增进对多模式交通网络中可及性公平问题的理解。

尽管我们的研究聚焦于素里市，但全球许多城市的生育率正在下降，预期寿命在上升[69]。人口结构向老年人口（即行动能力较低的人群）的转变将对确保医疗可及性公平带来重大挑战[70–72]。城市（再）开发并不总能在公共交通服务良好的区域进行，因此特定边缘化群体（尤其是老年人或低收入人群）对基本服务的可及性可能受到影响。从政策和交通规划的角度来看，不仅需要关注人口变化的量级，还需着力改善基础设施以及公共交通的时刻表安排，以应对某些社区社会人口统计结构的变化。

本研究侧重于分析人口统计学特征和可及性需求的变化，因此由于研究范围和缺乏适当数据，我们不得不假设交通网络和设施供给保持不变。然而，本文提出的方法可用于指导不同的基础设施投资策略，包括交通和卫生设施规划。基于代理的建模（ABM）等方法能够考虑多样化的社会行为决策，而非假设固定行为模式[73]，可与我们的合并聚类方法相结合，从而为具体案例研究提供更具细微差别的可达性分析。在城市分析中合理应用机器学习方法具有巨大潜力。