希尔排序的理解

0.思考

相比于直接插入排序和折半插入排序，有没有可以继续提高效率的方法？

  将要移动的元素移动一大步，即让它离排序完成后的最终位置更近一些。

想办法让我们在直接插入排序的时候，使得序列基本有序、个数较少并且当比较一次时，移动一大步，这就是希尔排序思想的出发点。

1.希尔排序

1.1希尔排序的基本思想

   先将整个待排记录序列分割成若干子序列，分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

     注：将记录序列分割成若干个子序列，这样就会：（1）每个序列的元素个数减少（2）分割成若干个子序列，这样进行交换时就可以移动一大步

   希尔排序算法的特点：

     1）缩小增量

     2）多遍插入排序

例1：

（1）以5为增量间隔分割成若干个子序列，也就是说81、35、41是分割好的第一个子序列：

将第一个子序列进行直接插入排序，结果为：

（2）接下来同样的以5间隔插入排序，结果如下：

 

到现在为止，每个子序列内部都是有序的了。可以看出，排序过程中每一个元素移动的步子比较大，这样可以快速接近最终位置。

（3）3间隔排序

（4）3间隔排序完成后，此时的元素序列已经基本有序了，最后我们进行1间隔插入排序，也就是说所以元素进行一次直接插入排序：

（5）到此为止，整个排序完成。

1.2希尔排序思路

（1）定义增量序列𝐷k:𝐷M>𝐷M−1>…>𝐷1=1

     ·刚才的例子中：D3=5，D2=3、D1=1

（2）1𝑛𝑌对每个𝐷k进行“𝐷k-间隔”插入排序（k=M，M-1，..1）

1.3希尔排序特点

·一次移动，移动位置较大，跳跃式地接近排序后的最终位置

·最后一次只需要少量移动

·增量序列必须递减的，最后一个必须是1

·增量序列应该是互质的

1.4希尔排序算法

主程序：

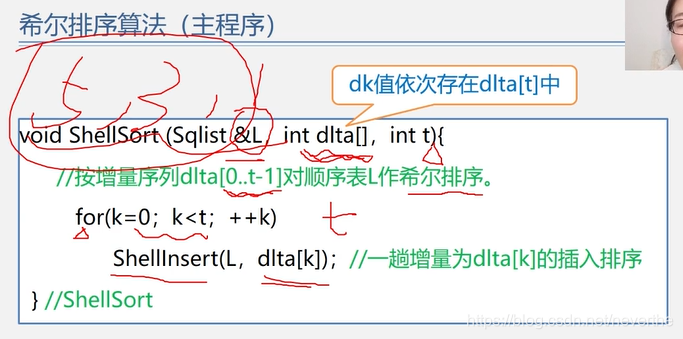
子函数：

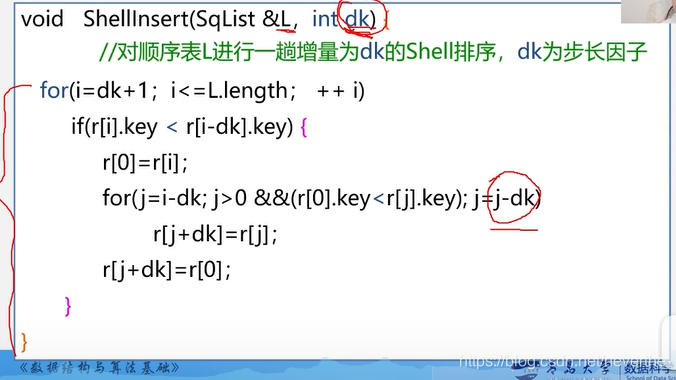
     上面代码中i=0处存储了哨兵，所以真正的序列是从1开始的，因此i是从增量+1开始的。

    在希尔排序的理解时，我们倾向于对于每一个分组，逐组进行处理，但在代码实现中，我们可以不用这么按部就班地处理完一组再调转回来处理下一组（这样还得加个for循环去处理分组）。比如[5,4,3,2,1,0] ，首次增量设gap=length/2=3,则为3组[5,2] [4,1] [3,0]，实现时不用循环按组处理，我们可以从第gap个元素开始，逐个跨组处理。同时，在插入数据时，可以采用元素交换法寻找最终位置，也可以采用数组元素移动法寻觅。

           在写代码时，我们从下标为第一个增量值处开始，进行跨组处理，而不是一组一组处理，如果要一组一组处理，则需要额外增加一个for循环，这样增加了算法的复杂度。例如，初始序列如下（无哨兵，故初始序列的下标从0开始，则i=增量）：

   若取增量为4，则分组结果为：{5，1，2}、{3，6}、{7，4}，{9，8}按照理解希尔排序的思路，我们应该先将{5，1，2}排好序后，再排{3，6}……但是这样做我们需要给整个程序加一个用于分组处理的for循环，增加了算法复杂度。因此我们这样考虑：从下标4处开始，减一个增量，先将这2个数排好序，然后继续往后跨组移动排序，接下来下标为5，那么我们减一个增量，继续排序……这样我们一直进行到整个序列的最后一个元素，此时我们就已经将所有的数排好序了。那么此时或许有一个疑问，这样做每次只交换了2个数，可是对于分组中有大于3个数的组，程序是怎么解决的呢？

     比如说{5，1，2}，第一次时我们对5和1进行了排序，接下来我们跨组依次往后排序，此时到了2这个元素，那么我们用2减去增量，又到了5那个位置，将这2个数排好序，然后我们利用for循环再继续减增量，对这2个数再继续排序，，一直到减增量后的值小于0为终止条件，说明此时2以及2之前的5和1，这3个数已经彻底排好了序，如果说序列再足够长，等到有一个数减去增量后又等于2，那么再利用for循环对这4个数再依次进行排序。

程序如下：

 

 

1.5希尔排序算法分析

    希尔排序算法效率增量序列的取值有关：

       ·Hibbard增量序列

                ·𝐷k=2k−1—相邻元素互质。 比如k从4开始，依次取15，7，3，1

   ·最坏情况：Tworst=O（n3/2）

          ·猜想：Tavg=O（n5/4）

         上述算法的平均程度只是一个估计或者猜想，因为根据增量序列来估算希尔排序的算法效率还属于数学上没有解决的一个难题。

1.6希尔排序算法的稳定性

          希尔排序法是一种不稳定的排序算法。举例：

1.7希尔排序算法分析总结  

 ·时间复杂度是n和d的函数：

            O（n1.25）~  O（1.6n1.25）——经验公式

 ·空间复杂度为 O（1）

 ·是一种不稳定的排序方法

     √如何选择最佳d序列，目前尚未解决

          √最后一个增量值必须为1，其它增量值无除了1之外的公因子

          √不宜在链式存储结勾上实现（因为链式存储结构找同一个增量的分组序列很麻烦）

参考：

1.排序之希尔排序(shell sort)

来自 <https://www.cnblogs.com/youzhibing/p/4889037.html>

2.排序算法研究之希尔排序（shell sort）

来自 <https://blog.youkuaiyun.com/qq_37466121/article/details/85957138>

3.图解排序算法(二)之希尔排序

来自 <https://www.cnblogs.com/chengxiao/p/6104371.html>

4.青岛大学王卓老师数据结构课。