最大流-最小割简介

最大流最小割问题在图像处理中的地位:

1.视觉问题可以看作是通过能量最小化进行的标号问题和一些其他问题,例如交互式图像分割问题。
2.能量最小化的标号问题又可以分为二元标号和多元标号问题。(多元标号问题又可以转化成二元标号问 题。)

3.二元标号问题又可以转化为求最小割问题。
4.最小割问题又可以转化为求最大流的问题，最大流问题是在多项式时间内的全局最优化.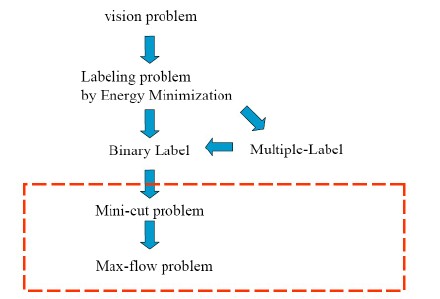

最大流-最小割问题都是用于S-T图中的.

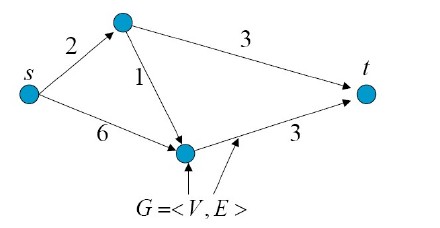
一个S-T图右下面几个要素:

1，一个源点和一个汇点
2，有向边，<i,j>是从i到j的。
3，每一条边都有一个非负的权值
4，容量cap(i,j)等于零，说明不存在边

S-T图举例:

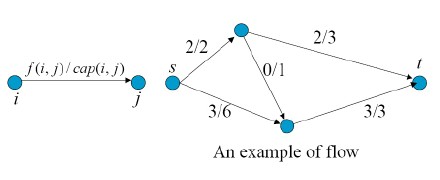
流的定义:

流是一个实函数f它赋予了每一条弧一个权值f(i,j)在下面条件的约束下，
---容量约束：权值f(i,j) <=cap(i,j)
---聚类平衡约束：

 

最大流是所有可能流函数中的有最大值的流。

 

最大流例子:管道网络中每边的最大通过能力即容量是有限的，实际流量也不一定等于容量，上述问题就是要讨论如何充分利用装置的能力，以取得最好效果（流量最大），这类问题通常称为最大流问题。

 

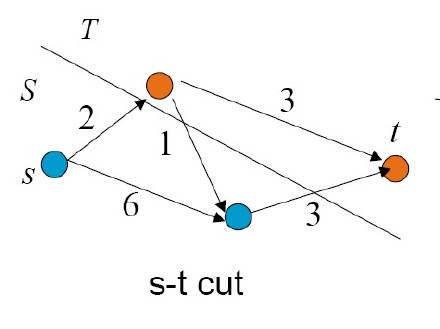
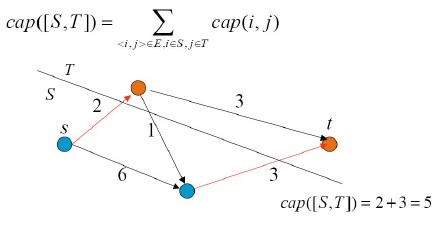
S-T割定义:

1，一个割是节点集合V的一个分割，分成了两个子集S和T.

2,当s属于S,v属于V时，这个割就是s-t切割

如图:

 

最小割的定义:

最小割是S-T切割中所有可能的S-T切割的能量最小的割

最大流和最小割的关系: 最大流<=最小割

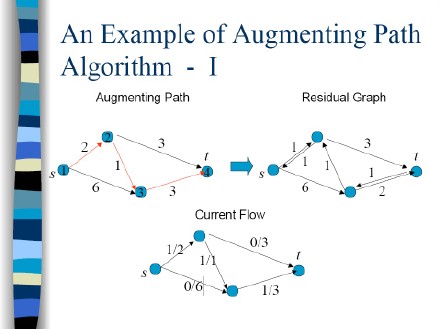
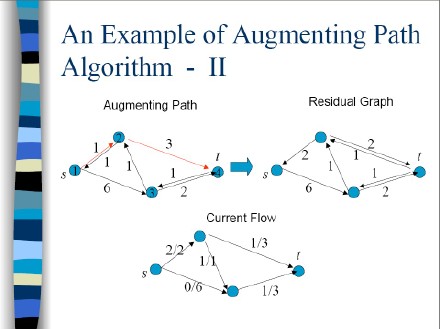
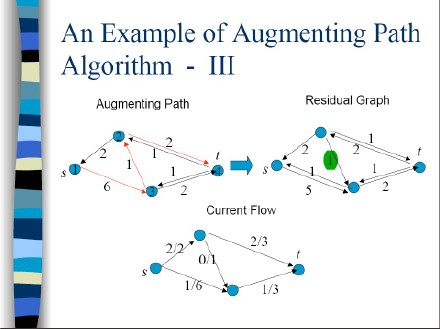
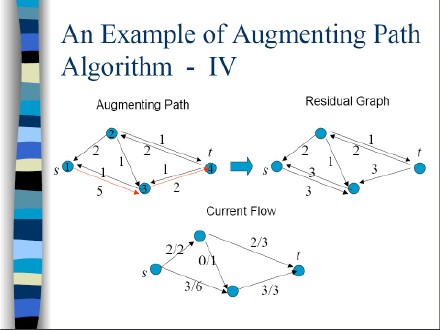
计算方法: