poj 1459 Power Network(网络流+dinic)-优快云博客

本文链接：https://blog.youkuaiyun.com/nealgavin/article/details/8671868

本文介绍了一种利用网络流算法解决电力网络中最大功率消耗问题的方法。通过建立发电站到消费者的模型，借助最大流算法计算电力网络能承载的最大功率消耗值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Power Network

Time Limit: 2000MS		Memory Limit: 32768K
Total Submissions: 19534		Accepted: 10300

Description

A power network consists of nodes (power stations, consumers and dispatchers) connected by power transport lines. A node u may be supplied with an amount s(u) >= 0 of power, may produce an amount 0 <= p(u) <= p _max(u) of power, may consume an amount 0 <= c(u) <= min(s(u),c _max(u)) of power, and may deliver an amount d(u)=s(u)+p(u)-c(u) of power. The following restrictions apply: c(u)=0 for any power station, p(u)=0 for any consumer, and p(u)=c(u)=0 for any dispatcher. There is at most one power transport line (u,v) from a node u to a node v in the net; it transports an amount 0 <= l(u,v) <= l _max(u,v) of power delivered by u to v. Let Con=Σ _uc(u) be the power consumed in the net. The problem is to compute the maximum value of Con.

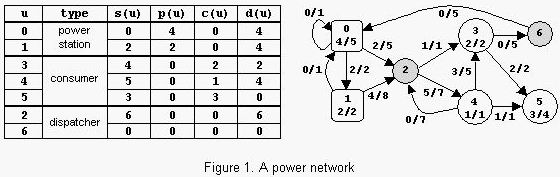
An example is in figure 1. The label x/y of power station u shows that p(u)=x and p _max(u)=y. The label x/y of consumer u shows that c(u)=x and c _max(u)=y. The label x/y of power transport line (u,v) shows that l(u,v)=x and l _max(u,v)=y. The power consumed is Con=6. Notice that there are other possible states of the network but the value of Con cannot exceed 6.

Input

There are several data sets in the input. Each data set encodes a power network. It starts with four integers: 0 <= n <= 100 (nodes), 0 <= np <= n (power stations), 0 <= nc <= n (consumers), and 0 <= m <= n^2 (power transport lines). Follow m data triplets (u,v)z, where u and v are node identifiers (starting from 0) and 0 <= z <= 1000 is the value of l _max(u,v). Follow np doublets (u)z, where u is the identifier of a power station and 0 <= z <= 10000 is the value of p _max(u). The data set ends with nc doublets (u)z, where u is the identifier of a consumer and 0 <= z <= 10000 is the value of c _max(u). All input numbers are integers. Except the (u,v)z triplets and the (u)z doublets, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.

Output

For each data set from the input, the program prints on the standard output the maximum amount of power that can be consumed in the corresponding network. Each result has an integral value and is printed from the beginning of a separate line.

Sample Input

2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)20
7 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 (2,4)7
         (3,5)2 (3,6)5 (4,2)7 (4,3)5 (4,5)1 (6,0)5
         (0)5 (1)2 (3)2 (4)1 (5)4

Sample Output

15
6

Hint

The sample input contains two data sets. The first data set encodes a network with 2 nodes, power station 0 with pmax(0)=15 and consumer 1 with cmax(1)=20, and 2 power transport lines with lmax(0,1)=20 and lmax(1,0)=10. The maximum value of Con is 15. The second data set encodes the network from figure 1.

Source

Southeastern Europe 2003

思路：网络流，建源点汇点，源点与发电站连权值为发电量，汇点与消费者间连权值为消费量，边就是线路传送能力。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int mm=310;
const int oo=1e9;
int dis[mm][mm],s,t,q[mm];
bool vis[mm],sig[mm][mm];
int n,np,nc,m;
bool bfs()
{ memset(vis,0,sizeof(vis));
  memset(sig,0,sizeof(sig));
  int l=0,r=1,z;q[l]=s;vis[s]=1;
  while(l<r)
  {
    z=q[l++];l%=mm;
    for(int i=0;i<=n+1;i++)
      if(!vis[i]&&dis[z][i])
    {
      vis[i]=1;sig[z][i]=1;
      q[r++]=i;r%=mm;
    }
  }
  if(vis[t])return 1;
  return 0;
}
int _min(int a,int b)
{
  if(a<b)return a;
  return b;
}
int dfs(int u,int sum)
{ int ret,s=sum;
  if(u==t)return sum;
  for(int i=0;i<=n+1;i++)
    if(sig[u][i])
  {
    ret=dfs(i,_min(sum,dis[u][i]));
    dis[u][i]-=ret;dis[i][u]+=ret;
    ///cout<<u<<"c"<<i<<" "<<ret<<endl;
    sum-=ret;
  }
  return s-sum;
}
int dinic()
{ int sum=0;
  while(bfs())sum+=dfs(s,oo);
  return sum;
}
int main()
{
  while(cin>>n>>np>>nc>>m)
  {int u,v,c;
    s=0;t=n+1;
    memset(dis,0,sizeof(dis));
    for(int i=0;i<m;i++)
    {
      while(getchar()!='(');
      scanf("%d,%d)%d",&u,&v,&c);
      dis[u+1][v+1]=c;
    }
    for(int i=0;i<np;i++)
    {
      while(getchar()!='(');
      scanf("%d)%d",&v,&c);
      dis[s][v+1]=c;
    }
    for(int i=0;i<nc;i++)
    {
      while(getchar()!='(');
      scanf("%d)%d",&u,&c);
      dis[u+1][t]=c;
    }
    /*for(int i=0;i<=n+1;i++)
      for(int j=0;j<=n+1;j++)
      if(dis[i][j])
      cout<<i<<" "<<j<<" "<<dis[i][j]<<endl;
    */cout<<dinic()<<"\n";
  }
}

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int oo=1e9;//无穷大
const int mm=1331603;
/**mm 表示边的最大数量，记住要是原图的两倍，在加边的时候都是双向的*/
const int mn=3030;
/**mn 表示点的最大数量*/
int src,dest,node,edge;
/**node 表示节点数，src 表示源点，dest 表示汇点，edge 统计边数*/
int ver[mm],flow[mm],next[mm];
/**ver 边指向的节点，flow 边的容量，next 链表的下一条边*/
int head[mn],work[mn],dist[mn],q[mn];
/**head 节点的链表头，work 用于算法中的临时链表头，dis 计算距离*/
/**初始化链表及图的信息*/
void prepare(int _node,int _src,int _dest)
{
  node=_node;src=_src;dest=_dest;
  for(int i=0;i<node;i++)head[i]=-1;edge=0;
}
/**增加一条u 到v 容量为c 的边*/
void addedge(int u,int v,int c)
{
  ver[edge]=v;flow[edge]=c;next[edge]=head[u];head[u]=edge++;
  ver[edge]=u;flow[edge]=0;next[edge]=head[v];head[v]=edge++;
}
/**广搜计算出每个点与源点的最短距离，如果不能到达汇点说明算法结束*/
bool bfs()
{
  int l=0,r=0;
  for(int i=1;i<=node;i++)dist[i]=-1;
  int i,u,v;
  dist[q[r++]=src]=0;
   for(l=0;l<r;l++)
    for(i=head[u=q[l]];i>=0;i=next[i])
    {
      if(flow[i]&&dist[v=ver[i]]==-1)
      {
        dist[q[r++]=v]=dist[u]+1;
        if(v==dest)return 1;
      }
    }
  return 0;
}
/**寻找可行流的增广路算法，按节点的距离来找，加快速度*/
int dinic_dfs(int u,int exp)
{
  if(u==dest)return exp;
  int v,tmp;
  /**work 是临时链表头，这里用i 引用它，这样寻找过的边不再寻找*/
  for(int&i=work[u];i>=0;i=next[i])//&i=work[u];删链优化
  if(flow[i]&&dist[v=ver[i]]==dist[u]+1&&(tmp=dinic_dfs(v,min(exp,flow[i])))>0)
  {
    flow[i]-=tmp;
    flow[i^1]+=tmp;
    /**正反向边容量改变*/
    return tmp;
  }
  return 0;
}
/**求最大流，直到没有可行流*/
int dinic_flow()
{
  int sum=0,data;
  while(bfs())
  {
    for(int i=0;i<node;i++)work[i]=head[i];
    while(data=dinic_dfs(src,oo))sum+=data;

  }
  return sum;
}
int main()
{
  int m,np,nc,n;
  int a,b,c,u,v;
  while(scanf("%d%d%d%d",&n,&np,&nc,&m)!=EOF)
  {
    prepare(n+2,0,n+1);
    for(int i=0;i<m;i++)
    {
      while(getchar()!='(');
      scanf("%d,%d)%d",&u,&v,&c);
     /// dis[u+1][v+1]=c;
      addedge(u+1,v+1,c);
    }
    for(int i=0;i<np;i++)
    {
      while(getchar()!='(');
      scanf("%d)%d",&v,&c);
      addedge(0,v+1,c);
      ///dis[s][v+1]=c;
    }
    for(int i=0;i<nc;i++)
    {
      while(getchar()!='(');
      scanf("%d)%d",&u,&c);
      addedge(u+1,n+1,c);
      ///dis[u+1][t]=c;
    }
    printf("%d\n",dinic_flow());
  }
}