01
引言
《易经》早就揭示出:物极必反,盛极必衰!阴阳总是不断交替的。股票市场也一样,涨跌互现,涨多了会出现调整,跌多了会出现反弹,因此我们看到K线组合总是红(阳)绿(阴)相间的。正是由于市场行情总是阴阳交替出现,交易者们才孜孜不倦地想通过择时(选股)来获取超额收益。指数的走势是各方资金博弈的结果,而博弈的过程存在一个时间的延续性,也就是说过去的走势对未来走向有一定的参考价值。尽管过去不能代表未来,但统计发现历史总是“惊人的相似”,比如“月份效应”。实际上,不少实证研究发现大多数市场存在“月份效应”,即存在某个或某些特定月份的平均收益率年复一年显著地异于其他各月平均收益率的现象。
公众号推文《A股指数图谱:是否有月份效应?》对A股历史走势、涨跌频率和“月份效应”进行了初步的量化分析和统计检验,发现各大指数在2月份具有统计上显著的正收益。本文在此基础上,对指数月度收益率及其波动性进行统计分析,根据指数月度收益率的历史表现构建简单的月度择时策略并进行历史回测。
02
月度收益率分析
数据获取
使用tushare在线获取指数(股票)日收益率数据,考虑到完整月份,数据期间选取2000年1月1日至2019年12月31日。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
%matplotlib inline
#正常显示画图时出现的中文和负号
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
import tushare as ts
def get_daily_ret(code='sh',start='2000-01-01',end='2019-12-31'):
df=ts.get_k_data(code,start=start,end=end)
df.index=pd.to_datetime(df.date)
#计算日收益率
daily_ret = df['close'].pct_change()
#删除缺失值
daily_ret.dropna(inplace=True)
return daily_ret
月度收益率情况
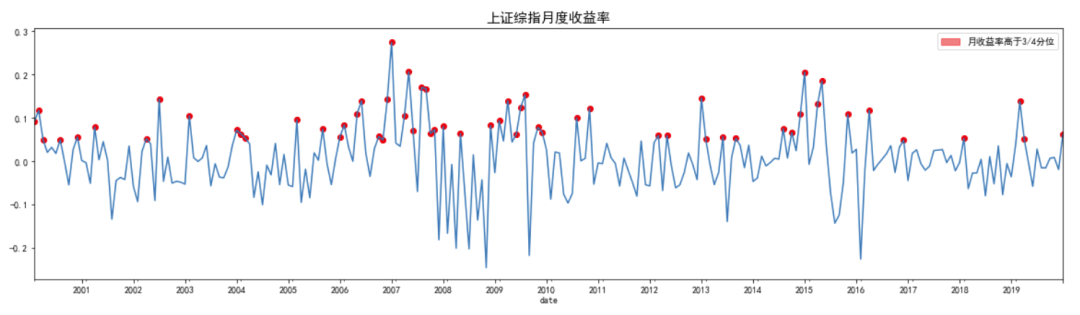
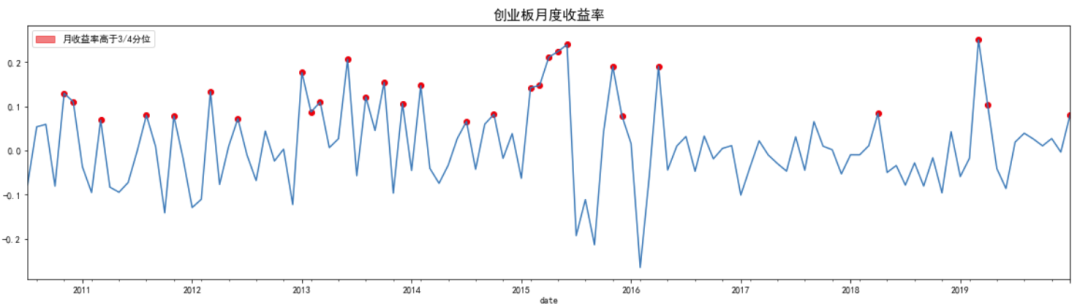
对指数月度收益率进行可视化分析,标注收益率高于四分之三分位数的点。
def plot_mnthly_ret(code,title):
daily_ret = get_daily_ret(code)
#月度收益率
mnthly_ret = daily_ret.resample('M').apply(lambda x : ((1+x).prod()-1))
#可视化
plt.rcParams['figure.figsize']=[20,5]
mnthly_ret.plot()
start_date=mnthly_ret.index[0]
end_date=mnthly_ret.index[-1]
plt.xticks(pd.date_range(start_date,end_date,freq='Y'),[str(y) for y in range(start_date.year+1,end_date.year+1)])
#显示月收益率大于3/4分位数的点
dates=mnthly_ret[mnthly_ret>mnthly_ret.quantile(0.75)].index
for i in range(0,len(dates)):
plt.scatter(dates[i], mnthly_ret[dates[i]],color='r')
labs = mpatches.Patch(color='red',alpha=.5, label="月收益率高于3/4分位")
plt.title(title+'月度收益率',size=15)
plt.legend(handles=[labs])
plt.show()
从图中不难看出,上证综指和创业板指数月度收益率围绕均线上下波动。
plot_mnthly_ret('sh','上证综指')
plot_mnthly_ret('cyb','创业板')
月波动率情况
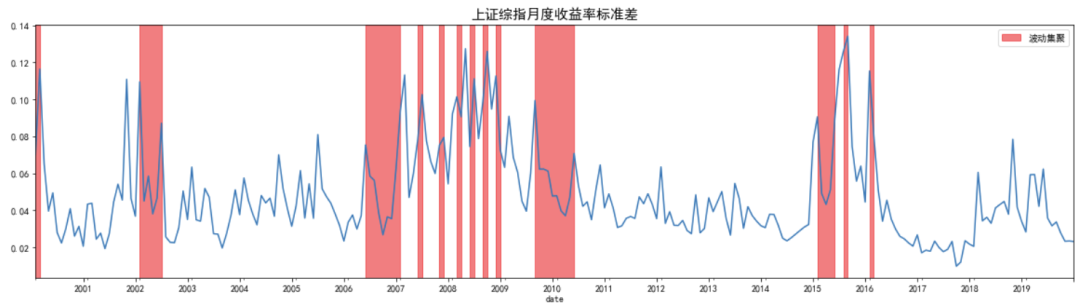
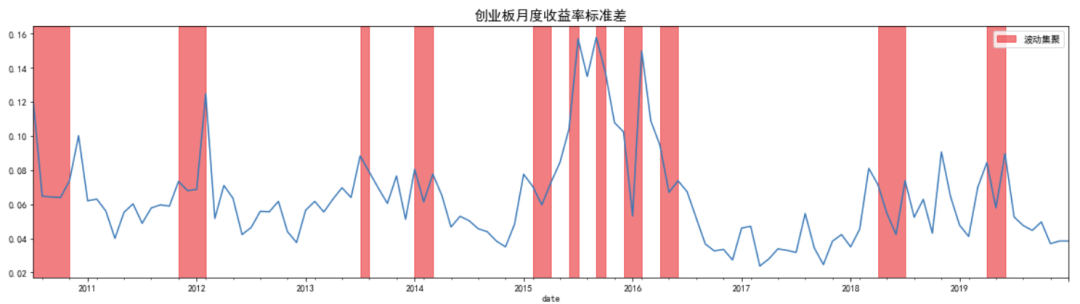
实证研究表明,收益率标准差(波动率)存在一定的集聚现象,即高波动率和低波动率往往会各自聚集在一起,并且高波动率和低波动率聚集的时期是交替出现的。
def plot_votil(code,title):
#月度收益率的年化标准差(波动率)
daily_ret=get_daily_ret(code)
mnthly_annu = daily_ret.resample('M').std()* np.sqrt(12)
plt.rcParams['figure.figsize']=[20,5]
mnthly_annu.plot()
start_date=mnthly_annu.index[0]
end_date=mnthly_annu.index[-1]
plt.xticks(pd.date_range(start_date,end_date,freq='Y'),[str(y) for y in range(start_date.year+1,end_date.year+1)])
dates=mnthly_annu[mnthly_annu>0.07].index
for i in range(0,len(dates)-1,3):
plt.axvspan(dates[i],dates[i+1],color='r',alpha=.5)
plt.title(title+'月度收益率标准差',size=15)
labs = mpatches.Patch(color='red',alpha=.5, label="波动集聚")
plt.legend(handles=[labs])
plt.show()
图中红色部门显示出,上证综指和创业板指数均存在一定的波动集聚现象。
plot_votil('sh','上证综指')
plot_votil('cyb','创业板')
月收益率均值
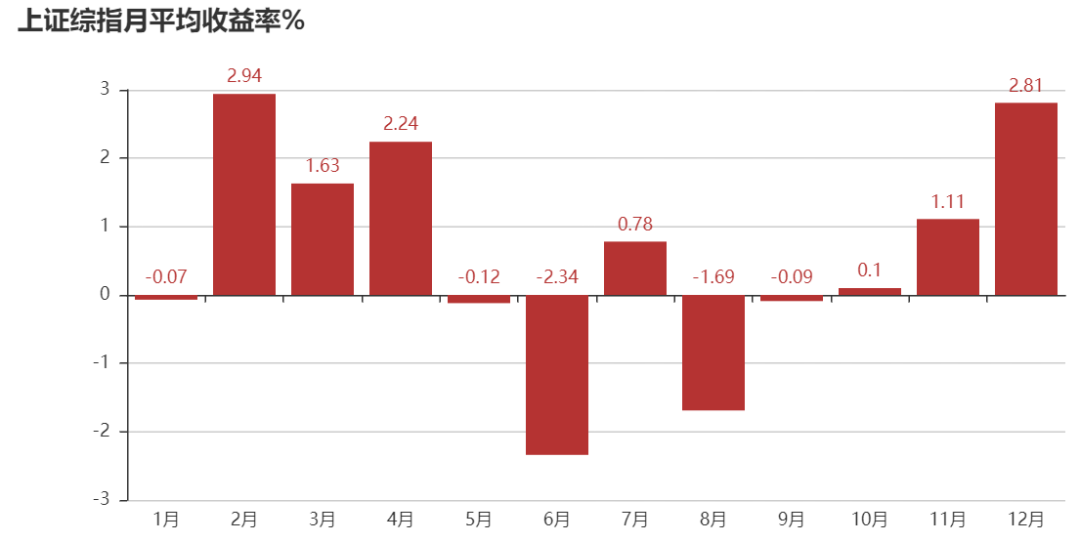
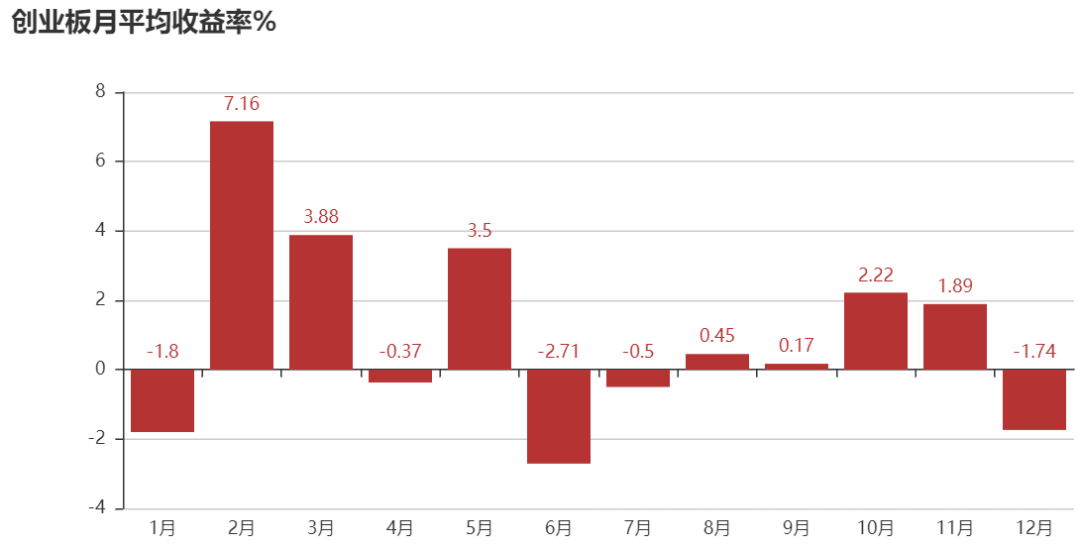
下面对月度收益率均值进行统计分析,图中显示某些月份具有正的收益率均值,而某些月份具有负的收益率均值,比如上证综指2月、3月、4月、11月、12月收益率均值大于1%,而6月和8月收益率均值小于-1%;创业板情况类似,但某些月份存在一定差异。
from pyecharts import Bar
#pyecharts是0.5.11版本
def plot_mean_ret(code,title):
daily_ret = get_daily_ret(code)
#月度收益率
mnthly_ret = daily_ret.resample('M').apply(lambda x : ((1+x).prod()-1))
mrets=(mnthly_ret.groupby(mnthly_ret.index.month).mean()*100).round(2)
attr=[str(i)+'月' for i in range(1,13)]
v=list(mrets)
bar=Bar(title+'月平均收益率%')
bar.add('',attr,v,
is_label_show=True)
return bar
plot_mean_ret('sh','上证综指')
plot_mean_ret('cyb','创业板')
03
月度择时策略回测
根据第二部分的统计分析,构建一个简单的月度择时策略并进行历史回测。即先对指数历史数据进行统计分析,计算月度收益率的历史均值,当月度收益率均值大于1%时做多改月,当月度收益率均值小于-1%时做空改月。
计算收益率均值
计算满足做多做空条件的月份,其余月份相当于空仓。
def month_ret_stats(code):
daily_ret = get_daily_ret(code)
#月度收益率
mnthly_ret = daily_ret.resample('M').apply(lambda x : ((1+x).prod()-1))
ret_stats=mnthly_ret.groupby(mnthly_ret.index.month).describe()
pnm=ret_stats[ret_stats['mean']>0.01].index.to_list()
nnm=ret_stats[ret_stats['mean']<-0.01].index.to_list()
return pnm,nnm
策略构建
def Month_Strategy(code,is_short):
daily_ret = get_daily_ret(code)
#月度收益率
mnthly_ret = daily_ret.resample('M').apply(lambda x : ((1+x).prod()-1))
#设计买卖信号
df=pd.DataFrame(mnthly_ret.values,index=mnthly_ret.index,columns=['ret'])
#做多月份
pnm,nnm=month_ret_stats(code)
print(f'做多月份:{pnm}')
df['signal']=0
for m in pnm:
df.loc[df.index.month==m,'signal']=1
#如果可以做空
if is_short==True:
for n in nnm:
df.loc[df.index.month==n,'signal']=-1
print(f'做空月份:{nnm}')
df['capital_ret']=df.ret.mul(df.signal)
#计算标的、策略的累计收益率
df['策略净值']=(df.capital_ret+1.0).cumprod()
df['指数净值']=(df.ret+1.0).cumprod()
return df
回测评价指标
def performance(df):
#代码较长,此处略
#将上述函数整合成一个执行函数
def main(code='sh',name='上证综指',is_short=False):
df=Month_Strategy(code,is_short)
print(f'回测标的:{name}指数')
performance(df)
plot_performance(df,name)
回测结果
上证综指情况:
#默认回测标的是上证综指
main()
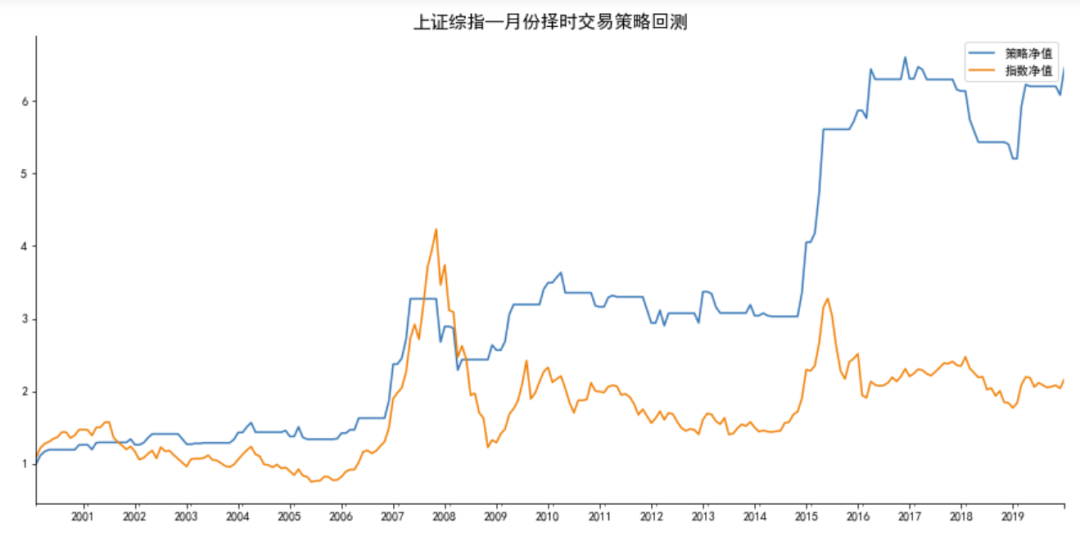
#不能做空时,结果如下:
做多月份:[2, 3, 4, 11, 12]
回测标的:上证综指指数
策略年胜率为:60.0%
策略月胜率为:58.0%
总收益率: 策略:545.53%,指数:116.88%
年化收益率:策略:9.77%, 指数:3.95%
最大回撤: 策略:30.0%, 指数:70.97%
策略Alpha: 0.08, Beta:0.43,夏普比率:2.04
main(is_short=True)
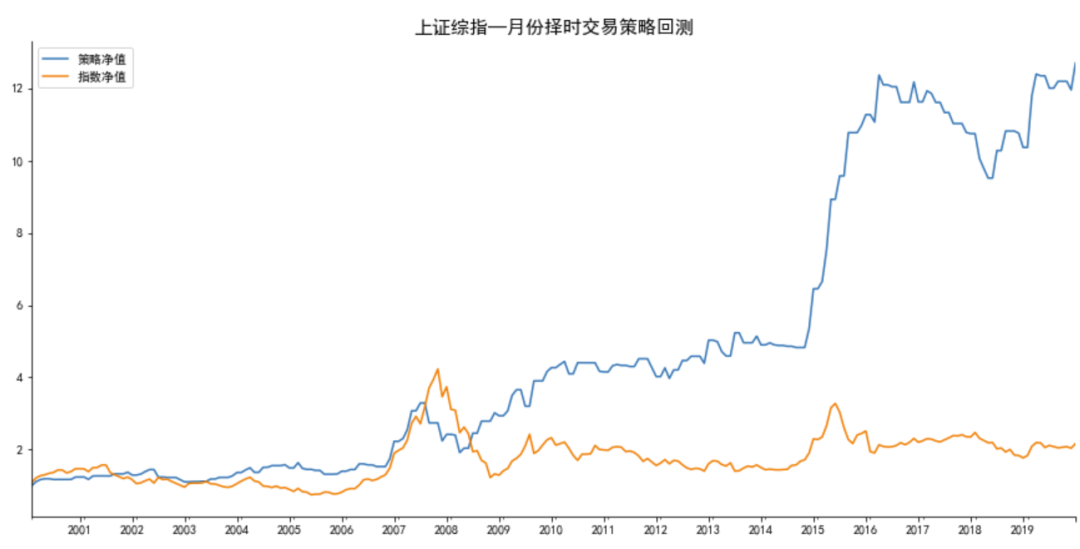
#可以做空时,结果如下:
做多月份:[2, 3, 4, 11, 12]
做空月份:[6, 8]
回测标的:上证综指指数
策略年胜率为:65.0%
策略月胜率为:55.71%
总收益率: 策略:1169.63%,指数:116.88%
年化收益率:策略:13.55%, 指数:3.95%
最大回撤: 策略:41.71%, 指数:70.97%
策略Alpha: 0.13, Beta:0.22,夏普比率:2.59
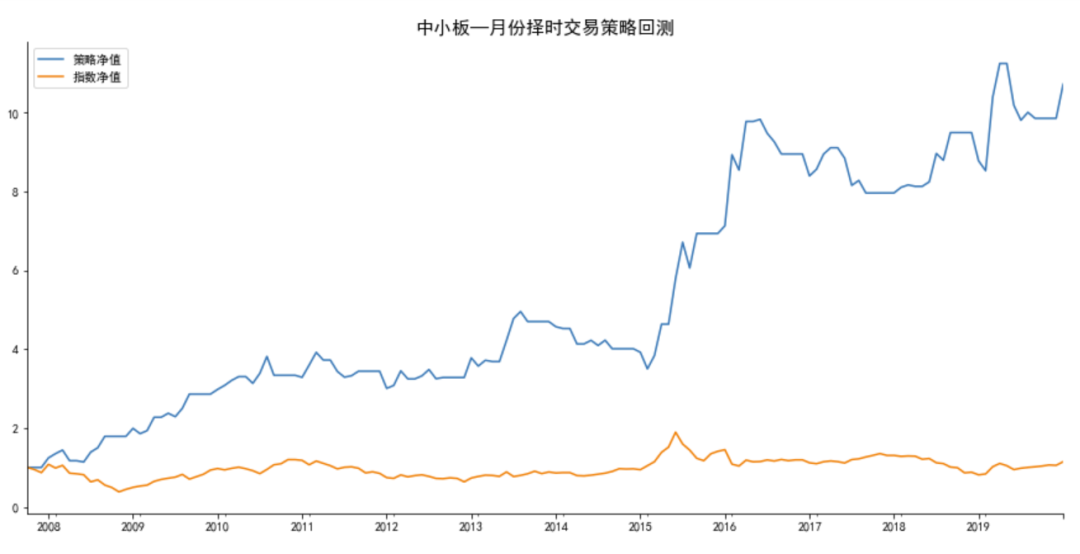
创业板指数情况:
main('cyb','创业板')
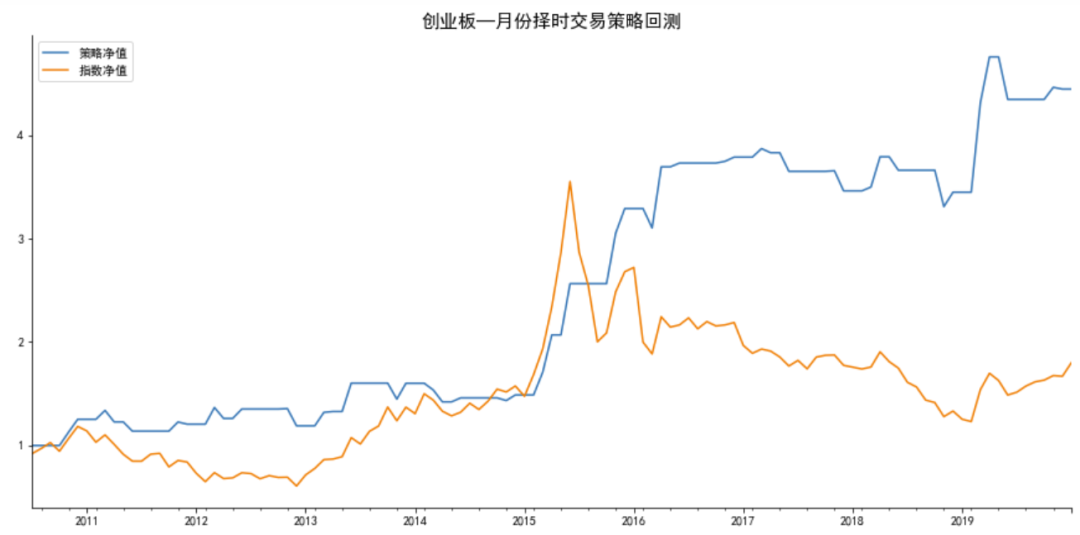
#不能做空时,结果如下:
做多月份:[2, 3, 5, 10, 11]
回测标的:创业板指数
策略年胜率为:50.0%
策略月胜率为:63.83%
总收益率: 策略:344.64%,指数:80.33%
年化收益率:策略:16.85%, 指数:6.35%
最大回撤: 策略:14.99%, 指数:65.34%
策略Alpha: 0.14, Beta:0.47,夏普比率:2.08
main('cyb','创业板',is_short=True)
#可以做空时,结果如下:
做多月份:[2, 3, 5, 10, 11]
做空月份:[1, 6, 12]
回测标的:创业板指数
策略年胜率为:70.0%
策略月胜率为:64.47%
总收益率: 策略:613.55%,指数:80.33%
年化收益率:策略:22.76%, 指数:6.35%
最大回撤: 策略:34.05%, 指数:65.34%
策略Alpha: 0.22, Beta:0.19,夏普比率:2.38
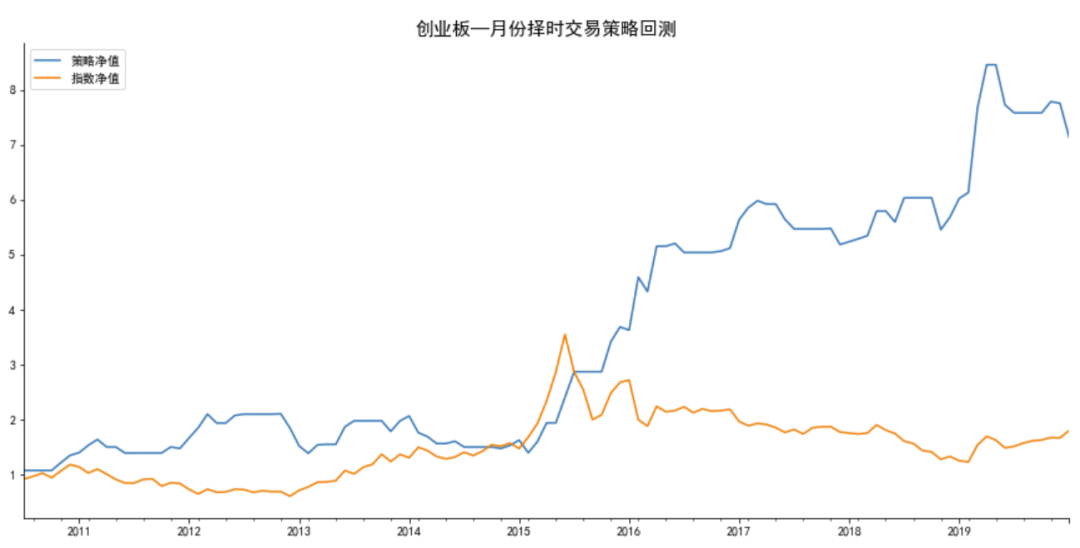
main('zxb','中小板')
#不能做空时,结果如下:
做多月份:[2, 3, 5, 7, 12]
回测标的:中小板指数
策略年胜率为:76.92%
策略月胜率为:62.3%
总收益率: 策略:350.15%,指数:14.57%
年化收益率:策略:12.97%, 指数:1.11%
最大回撤: 策略:22.63%, 指数:64.77%
策略Alpha: 0.12, Beta:0.46,夏普比率:1.93
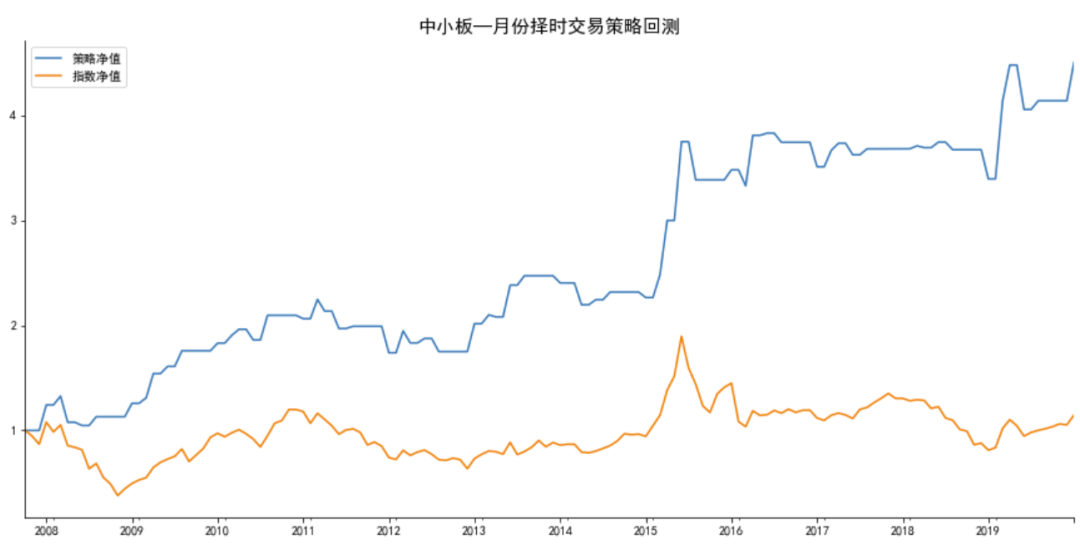
中小板指数情况:
main('zxb','中小板',is_short=True)
#可以做空时,结果如下:
做多月份:[2, 3, 5, 7, 12]
做空月份:[1, 6, 8]
回测标的:中小板指数
策略年胜率为:76.92%
策略月胜率为:58.76%
总收益率: 策略:972.68%,指数:14.57%
年化收益率:策略:21.21%, 指数:1.11%
最大回撤: 策略:29.35%, 指数:64.77%
策略Alpha: 0.21, Beta:0.16,夏普比率:2.66
04
结语
本文根据指数历史月度收益率的统计发现,某些月份具有正的收益率均值,而某些月份具有负的收益率均值,因此通过设定某个阈值进行择时,当月度收益率均值大于1%时做多改月,当月度收益率均值小于-1%时做空该月,从而构建了一个简单的月度择时策略。当然,这一策略存在一定的局限性,比如:(1)使用月度收益率样本量偏小,可能存在一定的偏差;(2)相当于使用了样本内数据进行拟合,可能存在过拟合问题。感兴趣的读者可以将样本分成两部分进一步考察,如2000-2016作为训练,2018-2020作为测试;(3)当市场环境和交易习惯发生较大变化后(如取消涨跌停板或延长交易时间等),过去的统计规律可能会失效等。本文对月度收益率进行统计分析并构建择时策略旨在于抛砖引玉,为大家考察和分析市场提供一个思路或角度,同时为大家熟练使用Python进行金融量化研究提供一个参考案例,以上分析不构成任何投资建议。

关于Python金融量化

专注于分享Python在金融量化领域的应用。加入知识星球,可以免费获取量化投资视频资料、量化金融相关PDF资料、公众号文章Python完整源码、量化投资前沿分析框架,与博主直接交流、结识圈内朋友等。





















 746
746










