GRAPH ATTENTION NETWORKS论文笔记

• 简单符号说明：

  h={h1⃗,h2⃗,…,hN⃗},hi⃗∈RF\boldsymbol h = \{\vec {h_1},\vec {h_2},\ldots,\vec{h_N}\},\vec {h_i} \in R^Fh={h1​​,h2​​,…,hN​​},hi​​∈RF 转换之前的节点特征矩阵，${\vec{h}}_i$是节点$i$的特征向量

  h′={h1′⃗,h2′⃗,…,hN′⃗},h⃗i∈RF′\boldsymbol h^{'} = \{\vec {h^{'}_1},\vec {h^{'}_2},\ldots,\vec {h^{'}_N}\},\vec h_i \in R^{F^{'}}h′={h1′​​,h2′​​,…,hN′​​},hi​∈RF′ 转换之后的节点特征矩阵

  $W\in R^{F^{{}^{\prime }}\times F}$ 层与层之间的转换矩阵

• 模型说明：

  1. 这篇文章提出的图注意力网络两点主要是根据中心节点其邻接点特征向量的取值来构建其对中心节点的影响程度，而不是像Kipf & Welling等人对邻接点统一对待。最后用于计算的邻接点也是一阶邻接点(直接相连)。

     每一个邻接点对于中心点的影响程度可以用图注意力系数$e_{ij}$表示,
     $$e_{ij}=a(\mathbf{W}\overrightarrow{h_i},\mathbf{W}\overrightarrow{h_j})$$
     a是注意力计算函数，对于任意节点我们只计算$j\in {\mathcal{N}}_i,{\mathcal{N}}_i$是节点$i$的邻接点集合。

     在这篇文章中，图注意力机制是一个单层前馈神经网络。简单的抽象理解如下：
     

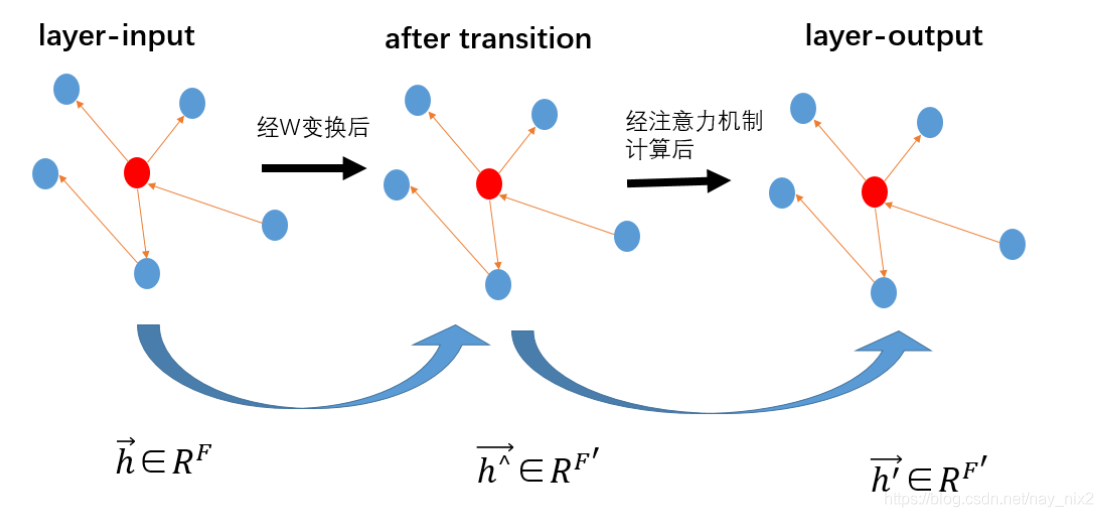
     为了使不同节点之间的注意力系数可比较，使用softmax函数对注意力系数进行规范化。
     $${\alpha }_{ij}=softma{x}_j(e_{ij})=\frac{exp(e_{ij})}{{\sum }_{k\in {\mathcal{N}}_i}exp(e_{ik})}$$

     具体的注意力计算时，这篇文章主要使用$\vec{a}\in R^{2F^{{}^{\prime }}}$（用于注意力计算的权值参数），以及LeakyReLu函数， 注意力系数的具体表达式如下：
     $${\alpha }_{ij}=\frac{exp(LeakyReLu({\vec{a}}^T[\mathbf{W}\overrightarrow{h_i}||\mathbf{W}\overrightarrow{h_j}]))}{{\sum }_{k\in {\mathcal{N}}_i}exp(LeakyReLu({\vec{a}}^T[\mathbf{W}\overrightarrow{h_i}||\mathbf{W}\overrightarrow{h_k}]))}$$

  2. 在聚合邻接点对中心节点的影响时，采用multi-head attention来聚合形成新的特征。
     $$\overrightarrow{h_i^{{}^{\prime }}}={\Vert }_{k=1}^K\sigma (\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{\mathbf{W}}^k\overrightarrow{h_j})$$
     注：经计算后，$h_i^{{}^{\prime }}\in R^{K{F}^{{}^{\prime }}}$

     最后一层(预测层)的聚合方式则采用取均值的方法进行，并延后使用激活函数
     $$\overrightarrow{h_i^{{}^{\prime }}}=\sigma (\frac{1}{K}\sum _{k=1}^K\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{\mathbf{W}}^k\overrightarrow{h_j})$$

  3. 模型过程：下面用来具体看一看每一层具体做了什么。

     每一层的输出：
     $$\begin{gathered} 每一层的输出(不用于预测时)：H^{l+1}=\left[\begin{array}{cccc}{H}_{11}^{l+1}& H_{12}^{l+1}& \cdots & H_{1,K{F}^{\prime }}^{l+1}\\ ⋮& ⋮& \ddots & ⋮\\ H_{N1}^{l+1}& H_{N2}^{l+1}& \cdots & H_{N,K{F}^{\prime }}^{l+1}\end{array}\right] \\ 每一层的输出(用于预测时)：H^{l+1}=\left[\begin{array}{cccc}{H}_{11}^{l+1}& H_{12}^{l+1}& \cdots & H_{1F^{\prime }}^{l+1}\\ ⋮& ⋮& \ddots & ⋮\\ H_{N1}^{l+1}& H_{N2}^{l+1}& \cdots & H_{N{F}^{\prime }}^{l+1}\end{array}\right] \end{gathered}$$

     ---

     每一层的输入：
     $$每一层的输入：H^l=\left[\begin{array}{cccc}{H}_{11}^l& H_{12}^l& \cdots & H_{1F}^l\\ ⋮& ⋮& \ddots & ⋮\\ H_{N1}^l& H_{N2}^l& \cdots & H_{NF}^l\end{array}\right]$$

     ---

     神经网络在每一层需要训练的参数，其中转换权值矩阵是直接的网络参数，而注意力矩阵是由神经网络参数$\vec{a}$计算而来。
     $$\begin{gathered} 转换权值矩阵：W=\left[\begin{array}{cccc}{W}_{11}& W_{12}& \cdots & W_{1F^{{}^{\prime }}}\\ ⋮& ⋮& \ddots & ⋮\\ W_{F1}& W_{F2}& \cdots & W_{F{F}^{{}^{\prime }}}\end{array}\right] \\ 注意力矩阵：att=\left[\begin{array}{cccc}at{t}_{11}& at{t}_{12}& \cdots & at{t}_{1N}\\ ⋮& ⋮& \ddots & ⋮\\ at{t}_{N1}& at{t}_{N2}& \cdots & at{t}_{NN}\end{array}\right] \end{gathered}$$

     ---

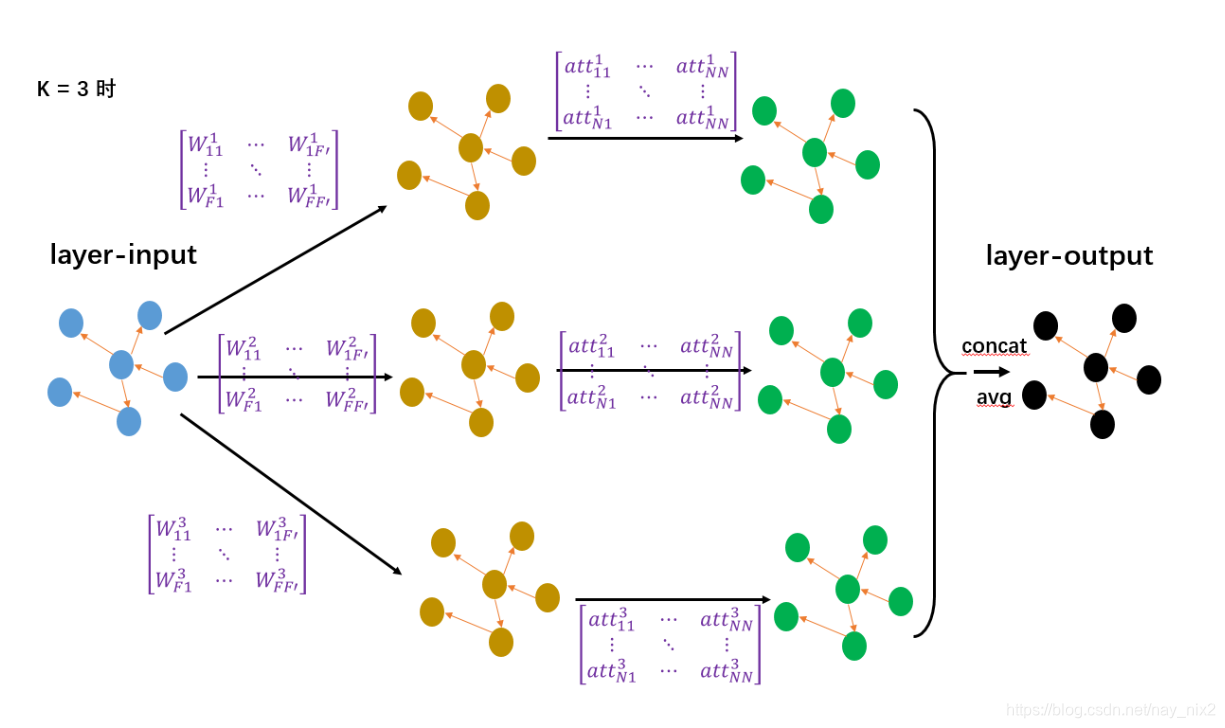
     每一层首先做的事就是通过转换矩阵将特征维度从$F->F^{\prime }$，之后再进行注意力计算，先由参数$\vec{a}$计算任意两条边的注意力系数，根据邻接矩阵显示的节点关系得到最终的注意力系数矩阵，再通过注意力系数矩阵与维度为F’的矩阵相乘得到新的特征矩阵，大小仍为$N\times F^{\prime }$。由于这篇文章采用的Multi-head attention策略，所以这样的网络有$K$层，可以分别得到$K$个$N\times F^{\prime }$的特征矩阵。最后，如果是中间层，那么仅需要连接这$K$个矩阵形成$N\times K{F}^{\prime }$的新特征矩阵，如果是最后一层，那么对这$K$个矩阵取均值仍然得到$N\times F^{\prime }$的矩阵。
     $$\begin{gathered} 当K=3时 \\ {H}_1^{{}^{\prime }}=H^l\times W_1,H_2^{{}^{\prime }}=H^l\times W_2,H_3^{{}^{\prime }}=H^l\times W_3 \\ {H}_1^{l+1}=at{t}_1\times H_1^{{}^{\prime }},H_2^{l+1}=at{t}_2\times H_2^{{}^{\prime }},H_3^{l+1}=at{t}_3\times H_3^{{}^{\prime }} \\ 当输出层不用于预测时,H^{l+1}=\left[\begin{array}{c}{H}_1^{l+1}⋮H_2^{l+1}⋮H_3^{l+1}\end{array}\right] \\ 当输出层用于预测时，H^{l+1}=\frac{1}{K}\sum _{i=1}^K{H}_i^{l+1} \end{gathered}$$

     图示说明如下：