因果推断（二）——混杂因子，D-分离，后门准则

最新推荐文章于 2025-06-08 01:51:17 发布
最新推荐文章于 2025-06-08 01:51:17 发布
阅读量9.9k 收藏 54
点赞数 21
CC 4.0 BY-SA版权
分类专栏： 因果推断 文章标签： 概率论 机器学习 算法 因果推断
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/naocanmani/article/details/120177230
本文深入探讨了因果推断中的关键概念——混杂因子、D-分离和后门准则。通过诺贝尔奖、巧克力和教育水平的例子，解释了混杂因子如何造成伪相关，并利用D-分离原则分析了如何在不同结构中判断变量的条件独立性。后门准则则提供了一种消除伪相关，揭示真正因果关系的方法。对于因果关系的正确分析，理解和应用这些原理至关重要。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

上次已经和大家分享了因果推断中的贝叶斯相关知识，今天这部分和大家分享因果推断中的混杂因子，D-分离，后门准则的相关内容。

图片先上例子

以上一篇中的诺贝尔奖和巧克力的事件为例，下图是他们三者的因果图，从图中可以看出这是一个叉式结构，即A和C相关。但是他们的相关性是通过“经济，教育水平”关联的，他们之间是伪相关，而B就是混杂因子，是它造成了A和C之间的伪相关。从字面上也很好理解，是因为B的存在导致我们对A和C之间的因果关系产生了混乱。

下图这种形式B也是confunder，即混杂因子。这种情况下，我们想要去发掘A和C的因果关系时，需要去除混杂因子，因为A->C的因果关系和A<-B->C造成的伪相关混合在一起了。

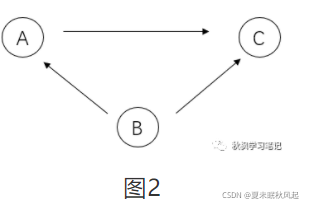
为了能正确分析因果关系，我们需要消除混杂，伪相关。

图片

最低0.47元/天 解锁文章

200万优质内容无限畅学
一文读懂因果推测、倾向模型（结合实例）
数据派THU
03-26 6139
原文题目：Propensity Modeling, Causal Inference, and Discovering Drivers of Growth作者：Edwin Chen翻译：张逸校对：卢苗苗本文共5400字，建议阅读9分钟。本文通过举例为你介绍因果推测方法、倾向建模及增长的驱动因素。在正文之前，先想象这样一个场景。你刚开始一份新工作，而且最近看了《僵尸世界大战》这部电影，正处于一种怀疑
因果系列文章（4）——拨开混杂的迷雾
jiey0407的博客
08-31 1099
本节沿袭上一节的内容，继续学习混杂、阻断、前门/后门路径等概念。抽烟的人容易导致肺癌，抽烟的人也容易出现黄手指。因为抽烟这个“共因”，“黄手指”和“肺癌”产生了关联，我们不难发现，手指黄的人很多都容易患肺癌。但是我们不能说，黄手指会导致肺癌，它俩并没有因果关系。这个“共因”也被称之为“混杂因子”（confounder）。在这个例子中，“抽烟”就是“黄手指”和“肺癌”的混杂因子，它让“黄手指”和“肺癌”出现了一种“伪相关”，这种伪相关也被称为“偏倚”（bias）。 图1：“抽烟”作为“黄手指”和“肺癌”的混杂
因果学习篇(1)-后门准则
chenzhiwen1998的博客
07-05 1573
因果学习是一门从纯理论的角度解释现实存在问题的学科，为统计学无法解决的问题提供理论支撑。
因果推断后门准则具体例子
最新发布
m0_54720701的博客
06-08 960
若直接拟合模型 (Y = \beta_0 + \beta_1 X + \epsilon)，系数(\beta_1) 可能仅反映相关性，而非因果性。假设原始数据中，服药组康复率为40%，未服药组为30%，表面上药物有效。通过后门调整，分层分析明确分离了年龄的影响，确保组内比较的公平性（即同年龄组内服药与未服药患者的差异仅由药物引起）。其中，(P(Y|do(X))) 表示干预X（强制服药）时Y的分布，通过对Z分层求和消除混杂。：研究某新型药物（X）对心脏病患者康复（Y）的因果效应，需排除年龄（Z）的混杂影响。
因果图模型与d-分离
小小程序猿的博客
06-04 4124
一般图都是由链结构(chain)、分叉结构(fork)、对撞结构(collider)这三种结构所组成，通过组合这三种结构，可以形成复杂图模型。 下面分别介绍这三种结构，以及对应的Rule. 1、链jiego
因果推断----去混杂
gpx33333的博客
01-31 1050
去混杂 混杂可以简单地定义为导致P(Y|X)≠P(Y|do(X))，即两个概率出现差异的所有因素。 为了去除X和Y中的混杂，我们只需要阻断它们之间的每个非因果路径，而不去阻断或干扰所有的因果路径就可以了。 更确切地说，我们将后门路径（back-door path）定义为所有X和Y之间以指向X的箭头为开始的路径；如果我们阻断了所有的后门路径（因为这些路径允许X和Y之间的伪相关信息在管道中流通），则我们就完成了对X和Y的去混杂。如果我们试图通过控制某一组变量Z来实现这一点，那么我们还需要确保Z的任何成员都不是X
因果推断（四）——后门调整、前门调整、逆概率加权
夏未眠秋风起的博客
09-15 1万+
在因果推断（三）中，我们介绍了干预的相关概念，在本文中，我们对一些方法进行介绍，这些方法可用于利用干预分析变量之间的因果关系。 在因果推断（三）中，我们得出了调整公式，如上式。假设PA为A节点的所有父节点的集合，则上 式可以修改为 其中b为PA所有可能的取值 后门调整 回顾后门准则的定义：对于X到Y的路径中，如果Z集合中的节点不是X的后代节点，并且以Z为条件会阻断所有X和Y之间的后门路径，则Z满足（X,Y）的后门准则。如果B满足后门准则，则后门调整公式就是我们在...
推荐系统+因果推断（一）——KDD2021推荐系统中去除混淆缓解偏差放大
夏未眠秋风起的博客
09-21 4839
今天和大家分享一篇因果推断和推荐系统结合的文章。因果推断在推荐系统中主要应用于用户增长、定价算法以及纠偏等领域，这篇文章属于纠偏领域。主要用到了我们前面因果推断（二）和因果推断（四）中提到的混杂和后门调整等内容，有不熟悉的小伙伴可以翻看前面的文章，好啦，进入正题。 背景 推荐系统中通常用于学习的数据是不平衡的。由于我们是从用户的历史点击或者转化数据中进行学习，因此通常会面临这样一个问题：对于推荐过的商品我们会认为用户是很感兴趣的，所以很可能会继续给他推荐，而对于没有推荐过的商品，...
因果推断（三）——结构因果模型、干预、辛普森悖论
夏未眠秋风起的博客
09-10 7341
主要内容 结构因果模型 干预 辛普森悖论 调整公式 结构因果模型（Structural Causal Model, SCM） 定义：结构因果模型被定义为一个有序三元组<U,V,f>，U为外生变量，即有模型外部因素决定，外生变量不能是其他变量的后代；V为内生变量，即由模型内部因素决定，内生变量至少是一个外生变量的后代；f为一组方程，通过f可以用外生变量推导出内生变量的值 SCM包含图结构和变量，简单的例子如下： 以因果推断（二）中的诺贝尔奖和巧克力的事
SIGIR‘21因果推断——不要把流行度偏差一棍子打死Causal Intervention for Leveraging Popularity Bias in Recommendation
夏未眠秋风起的博客
10-08 2288
Causal Intervention for Leveraging Popularity Bias in Recommendation https://arxiv.org/pdf/2105.06067.pdf 背景 本文所提方法针对召回阶段所用方法。之前的工作考虑的是如何缓解流行偏差带来的问题，包括IPS，causal embedding等，而本文考虑的是直接缓解流行偏差而不是流行偏差带来的影响。并且本文考虑到“不是所有流行偏差都是有害的”，流行的item可以反映这个item的趋势和内在特性。而我们..
后门准则(Backdoor Criterion)与前门准则(Frontdoor Criterion)
热门推荐
小小程序猿的博客
07-12 2万+
1.后门准则 定义：给定有向无环图（DAG）中一对有序变量（X，Y），如果变量集合Z（可以为空）满足： Z中没有X的后代节点。 Z阻断了X与Y之间的每条含有指向X的路径。 满足以上两点的Z，就称Z满足关于（X，Y）的后门准则。 如果变量集合Z满足（Ｘ，Ｙ）的后门准则，那么X对Y的因果效应可以由下面的公式计算。 证明如下： 一般而言，我们希望节点Z最好可以满足下面这些条件： 阻断X和Y之间的所有伪路径（即所有指向X的路径）。 保持所有X到Y的有向路径不变。 不会产生新的伪路径。（例.
因果图—后门准则
qq_26430933的博客
01-13 1642
1.贝叶斯网络概率图 1.1 链式法则 P(x1,x2,⋯ ,xn)=∏i=1nP(xi∣x1,x2⋯xi−1)P(x_1,x_2,\cdots,x_n) = \prod_{i=1}^n P(x_i|x_1,x_2 \cdots x_{i-1}) P(x1​,x2​,⋯,xn​)=i=1∏n​P(xi​∣x1​,x2​⋯xi−1​) 举例：P(x1,x2,x3,x4)=P(x1)∗P(x2∣x1)∗P(x3∣x1,x2)∗P(x4∣x1,x2,x3)P(x_1,x_2,x_3,x_4) = P(x_1)*P
统计因果推理入门：D-分离
xjy9866的博客
04-22 817
如果一条路径被一组条件节点Z阻断，当且仅当（两个条件有一个成立即可）：1.路径p包含链结构A → B → C,或分叉结构A ← B → C，且中间节点B在Z中（即以B为条件）2.路径p包含一个对撞结构A → B ← C，且对撞节点B及其子孙节点不在Z中。（以对撞节点为条件时，会解除阻断）
因果推断 - 干预
lch的博客
04-19 6872
目录基础知识干预前门准则、后门准则后门调整逆概率加权前门调整 版权：转载前请联系作者获得授权。 声明：部分内容出自因果关系之梯，已获得原作者授权。 参考书籍：《The Book of Why》——Judea Pearl 基础知识 干预 定义：将因果图中结点XXX的值修改为xxx，记为do(X=x)do(X=x)do(X=x)，可以简写为do(x)do(x)do(x)。 性质：在对结点X进行干预时，会删除因果图中指向X的边。 与“以变量为条件”的区别： 表现形式：P(Y=y∣X=x)P(Y=y | X=x
D-Separation(D分离)-PRML-8.22-Graphical Model 五 18 by 小军
weixin_30295091的博客
06-06 366
D-Separation(D分离)-PRML-8.22-Graphical Model 五18by小军 一、引言 在贝叶斯网络的学习过程中，经常会遇到（D-Separation）D-分离这个概念，D-分离是寻找网络节点之间的条件独立性的一种方法或者说一种问题的简化处理的技巧。采用D-分离技术，在用贝叶斯网络进行预测，诊断推理等方面，可以提高计算速度，减少计算复杂性。 D-Sep...
概率图模型（PGM）里的有向分离（D-separation）
远方的橄榄树
09-09 1万+
有向分离（Directed Separation）是概率论中的概念， 有向分离（D-separation）： 如果集合Z阻塞X到Y中的任何一条通路（path），则称在这个DAG里，集合Z有向分离X和Y。也称Z 为X和Y的切割集。 如果一个路径不是有向分离的，则称其为有向连接的（D-connected）。 整体markov性揭示了图论和概率论之间的联系。
因果推断笔记——数据科学领域因果推断案例集锦（九）
素质云笔记
09-09 2万+
2 腾讯看点：视频笔记 ​ 2.1 观测数据 、 实验数据的理论介绍 ​ ![image.png](https://img-blog.csdnimg.cn/img_convert/c66bdbcdd86d5031040f51924397952d.png#clientId=u8e2473a0-856a-4&from=paste&height=746&id=ud2728b80&margin=[object Object]&name=image.png&origin
控制研究的混杂因素（Confounder）
leroylee7的博客
12-18 2万+
高高兴兴地写完一篇 SCI，投稿，苦苦等待好久，却只等来审稿人的一句话：你有控制研究的混杂因素（Confounder）吗？ 额，什么是混杂因素？又该如何控制？ 其实，混杂因素的控制在研究设计阶段就应该注意。 今天，笔者就从「什么是混杂因素」、「为什么要控制混杂因素」以及「该如何控制混杂因素」，这三方面来分享一下。 1、什么是混杂因素？ 混杂因素，指的是除了研究因素以外，其他所有可能会影响结局的因素（包括已知和未知的）。 混杂因素与结局事件、暴露/处...
因果 前门准则 后门准则
01-01
### 因果推断中的前门准则与后门准则 #### 后门准则概念 在因果图模型中，后门路径是指那些能够使处理变量X和结果变量Y之间的关联变得混淆的间接路径。为了消除这种混淆因素的影响，需要阻塞所有的后门路径。具体来说，如果一组变量Z满足以下条件，则认为这组变量可以用来控制后门路径： - Z包含了所有指向X的箭头起点节点； - 对于任何碰撞节点W（即形如A→W←B），要么不在Z内，要么其后代也不在Z内。 通过调整这些变量，可以在观察数据上实现如同随机对照试验的效果，从而得到无偏倚的因果效应估计[^4]。 #### 前门准则概念 当无法直接测量某些混杂因子时，可以通过寻找中介变量来构建所谓的“前门”。所谓前门标准指的是，在给定条件下，某个特定集合M满足如下三个性质即可视为有效的前门调节器： - M完全介导了从X到Y的所有直接影响； - 不含来自U对M的未受控入边； - 所有的后门通路都被适当封闭。 利用这样的中间机制，即便存在未知或不可测得的因素干扰原始因果链，仍然有可能评估出真实的因果关系强度。 #### 应用实例 考虑药物治疗效果的研究场景下，假设我们想要探究某种新药对于患者康复速度的具体影响。此时可能会遇到各种潜在的混杂因素，比如患者的年龄、性别差异或是其他健康状况等。按照上述原则选取合适的协变量集合作为后门控制器；而如果是探讨广告投放对企业销售额增长的作用力大小，则可借助销售量变化趋势作为前门媒介来进行分析[^2]。 ```python import numpy as np from sklearn.linear_model import LinearRegression def estimate_causal_effect(X, Y, confounders=None): """ Estimate causal effect using linear regression with or without controlling for confounders. Parameters: X (array-like): Treatment variable. Y (array-like): Outcome variable. confounders (array-like, optional): Confounding variables to control for. Returns: float: Estimated average treatment effect on the treated. """ model = LinearRegression() if confounders is not None: features = np.column_stack((X, confounders)) else: features = X.reshape(-1, 1) model.fit(features, Y) ate = model.coef_[0] return ate ```
评论 3
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值