[daily paper 8]2023 03 06 2016 53 Merge based SpMV using the CSR storage format

论文链接

这篇论文是来自NVDIA公司，非常短，只有两页，直接看有点难理解。里面一个很重要的思想来自于另一篇论文“Merge Path - Parallel Merging Made Simple”（论文链接），我先讲这个。

这篇论文讲的是如何将两个有序数组合并的操作并行化。一个很直觉的方式是将两个数组都分成两半，然后分别归并，最后将归并的结果连接到一起。但是这个方法是错的，比如A = 1, 2, 3, 4，B = 7, 8, 9, 10，分成两半分别归并，得到1, 2, 7, 8和3, 4, 9, 10，连到一起变成1,2,7,8,3,4,9,10，并不是升序的。所以选好切分点很重要，选不好结果就是错的。

文中给出了一种分割的方法，并且给出了很直观的证明。

首先将两个有序数组排成如下形状：

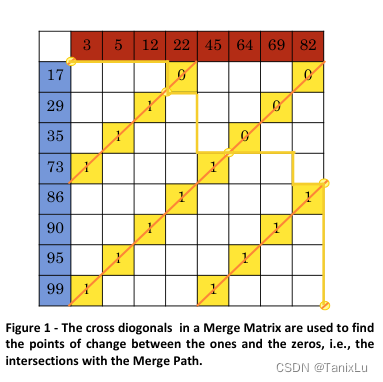
从左上角开始，比较两数组对应元素哪个小，谁小往哪个方向拐，只能向右或者下。这样就形成了一条路径，叫做merge path。在merge path上任取一点，比如(1,3)这个点吧，对应一个矩形，也对应两数组的几个数字，17和3、5、12。这样的切分是可以的，这个merge path就是归并的道路，每次把最小的拿出来，所以17和3、5、12比其他所有数字都小。

那么我们划一条副对角线，怎么知道和merge path的交点在哪呢？来看下面这一张图：

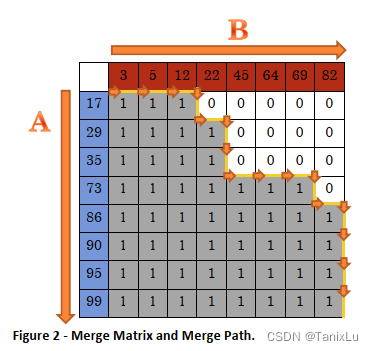
我们把这个矩阵（叫做merge matrix）中填上1或者0，1代表对应位置元素A大于B，0代表对应位置元素B大于A。我们会发现merge path恰好就沿着所有1的边。其实也很好理解，只有右下角位置在矩阵内，且为0的时候，才会向下拐。

我们观察一条副对角线，发现每条副对角线都是一段连续的1和一段连续的0（都有可能为空）。如Figure 1刚才举得那个例子，副对角线上是1,1,1,0。

知道这样的性质之后，就可以用二分查找很高效地在副对角线上查找和merge path的交点，以完成分割。

论文后面讲了如何更好地利用cache。假设cache大小为C（能存C个A或B的元素）。那么设L=C/3，每次切L长度的A+B，如下图中较长的黄线。然后切出来的部分比较少，所有操作是可以全在cache中完成的。切出来的部分是黑线框出来的部分，如第一个3x4的矩阵。将这个矩阵分成p个部分，p为处理器数量，实现并行。这种方法针对的是PRAM类的系统，也就是说有一个共享的内存，和一个共享的cache。

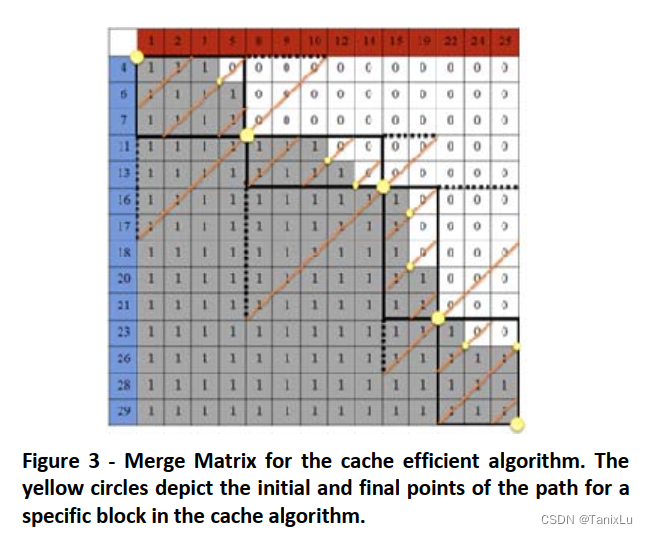
好了，可以讲会原来那篇论文了，该论文用的是CSR格式，这样就避免了格式转化带来的overload：

它的目标是将values这个代表所有非零元素的数组等量切分，以求达到不错的负载均衡。这篇论文是针对GPU的，需要提前说明一下。然后论文中给出了这一张图：

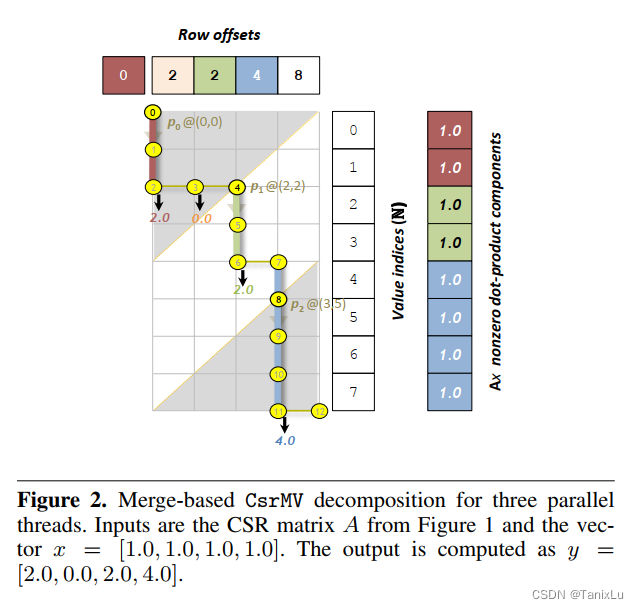
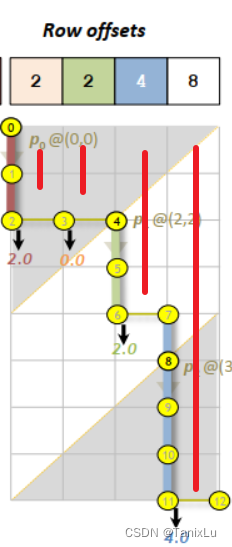
如果没看过上面那篇论文还真看不明白。这个CsrMV把Row offsets和value indices摆在了一起，形成一个矩阵。它这样做的原因是，CSR格式就是一个row offset，对应一段value indices，可以想象一下拿掉一个row offset，就拿掉一组value indices，这个和归并是有一点像的。在CsrMV的图中，消耗value index是往下走，消耗row offset是往右走。这里面填的1、0就不像上一篇论文那样了，而是看纵坐标j和row offset的关系。看我下面这张图，row offsets是2, 2, 4, 8，下面的"0"的个数也是2, 2, 4, 8，这样我们又可以使用二分查找来找交点了。切分过后可能还有把一row切到不同核心的情况，后面算完还要加起来。

总结一下，这篇论文借助merge path（merge matrix）的思想，完成了对稀疏矩阵非零元的直接划分，以实现负载均衡。缺点是针对不同特征的矩阵，CSR可能依旧有压缩的空间，没有突破内存带宽的瓶颈。