PCA介绍以及简单实例

最新推荐文章于 2022-01-04 20:11:21 发布
原创 最新推荐文章于 2022-01-04 20:11:21 发布 · 1.7k 阅读 · 5 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#PCA

目录

  • 数学基础

  • 基变换

  • 特征值，特征向量

  • 线性变换

  • 协方差

  • 矩阵对角化

  • PCA简单实例

简介

PCA全称Principal Component Analysis，即主成分分析，是一种常用的数据降维方法。它可以通过线性变换将原始数据变换为一组各维度线性无关的表示，以此来提取数据的主要线性分量。

数学基础
向量的表示
  • 内积

a 1 , a 2 , ⋯   , a n ) T ⋅ ( b 1 , b 2 , ⋯   , b n ) T = a 1 b 1 + a 2 b 2 + ⋯ + a n b n a_{1},a_{2},\cdots ,a_{n})^T\cdot (b_1,b_2,\cdots,b_n)^T = a_1b_1+a_2b_2+\cdots+a_nb_n a1​,a2​,⋯,an​)T⋅(b1​,b2​,⋯,bn​)T=a1​b1​+a2​b2​+⋯+an​bn​

几何解释

A ⋅ B = ∣ A ∣ ∣ B ∣ c o s ( a ) A\cdot B = \left | A \right |\left | B \right |cos(a) A⋅B=∣A∣∣B∣cos(a)

设向量B的模维1 ， 则A与B的内积值等于A向B所在的直线投影的矢量长度
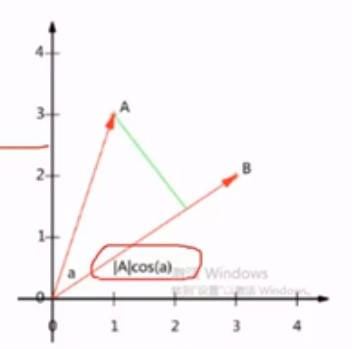
af19c30e-a602-44d2-9bc4-edb27d5a7ac4.jpg

向量表示为（3,2）

实际上表示线性组合

x ( 1 , 0 ) T + y ( 0 , 1 ) T x(1,0)^T + y(0,1)^T x(1,0)T+y(0,1)T （1,0）就是X轴，（0,1）就是y轴

基变换

基是正交的（即内积为0 ， 或者直观的说相互垂直）

要求： 线性无关

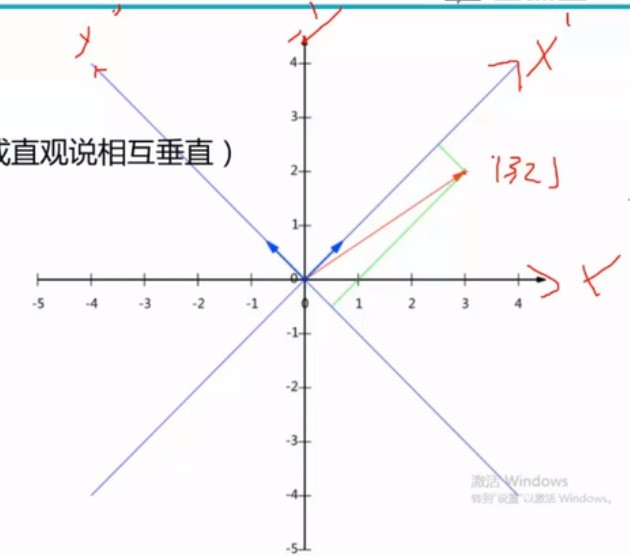
线性无关.jpg

将（3,2）映射到新的基上 xy

变换 ： 数据与一个基做内积运算，结果作为第一个新的坐标分量，然后与第二个基做内积运算，结果作为第二个新坐标的分量

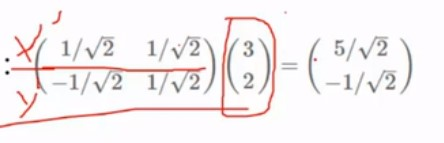
将数据（3,2）映射到基中的坐标

3-2.jpg

最低0.47元/天 解锁文章
PCA例子
you-know-who的博客
11-05 7136
 PCA（Principal Components Analysis）即主成分分析，是图像处理中经常用到的降维方法。 例子具体步骤 1、原始数据： 为了方便，我们假定数据是二维的，借助网络上的一组数据，如下： x=[2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1]T y=[2.4, 0.7, 2.9, 2.2, 3.0, 2.7, 1.6, 1.1...
PCA详解
chenjunheaixuexi的博客
06-04 1万+
PCA，即主成分分析，通常用于数据的降维、去噪，可以有效地解决过拟合问题，提高训练效率
PCA算法实例
10-12
此为MATLAB程序，里面详细介绍了PCA主成分分析，并附有数据，希望对大家有帮助。
PCA实例
阳光zfc
06-19 1277
　下面举一个简单的例子，说明PCA的过程。　　　　假设我们的数据集有10个二维数据(2.5,2.4), (0.5,0.7), (2.2,2.9), (1.9,2.2), (3.1,3.0), (2.3, 2.7), (2, 1.6), (1, 1.1), (1.5, 1.6), (1.1, 0.9)，需要用PCA降到1维特征。　　　　首先我们对样本中心化，这里样本的均值为(1.81, 1.91),...
PCA的应用示例
热门推荐
Work Hard, Play Harder!
08-13 3万+
在 PCA 详细算法介绍 （http://blog.youkuaiyun.com/watkinsong/article/details/38536463） 中， 因为篇幅问题 没有给出详细的代码示例， 这里给出代码示例。 通过对人脸图像进行降维深入了解PCA算得使用。 首先看一下数据集， 我们有12张人脸图像， 用10张人脸训练PCA降维矩阵， 剩下的两张可以用作测试。
Matlab基于PCA算法的简单图像人脸识别算法源码.zip
03-12
《Matlab基于PCA算法的简单图像人脸识别算法源码.zip》是一份基于Matlab实现的、采用PCA（主成分分析）算法的简单图像人脸识别资源。该源码通过提取人脸图像的主要特征，将高维的人脸图像数据降维到低维空间，从而...
matlab pca可视化,[转]PCA的介绍，实例及绘图
weixin_28799111的博客
03-19 1172
PCA的介绍多元统计分析中普遍存在的困难中，有一个困难是多元数据的可视化。matlab的plot可以显示两个变量之间的关系，plot3和surf可以显示三维的不同。但是当有多于3个变量时，要可视化变量之间的关系就很困难了。幸运的是，在一组多变量的数据中，很多变量常常是一起变动的。一个原因是很多变量是同一个驱动影响的的结果。在很多系统中，只有少数几个这样的驱动，但是多余的仪器使我们测量了很多的系统变...
精选资源
主成分分析：为 PCA 新手提供了一步步进行 PCA 的简单代码以及解释。-matlab开发
05-29
下面我们将详细探讨PCA的基本步骤，并通过MATLAB代码实例来理解这一过程。 1. 数据预处理：在进行PCA之前，通常需要对数据进行标准化或归一化，确保所有特征具有相同的尺度。MATLAB中的`zscore`函数可以实现这一点...
使用协方差矩阵的特征向量PCA来处理数据降维
昕友软件博客
10-23 372
取2维特征，方便图形展示 import matplotlib.pyplot as plt from sklearn.decomposition import PCA from sklearn.datasets import load_iris data = load_iris() y = data.target X = data.data pca = PCA(n_c...
python主成分分析_Python机器学习笔记：主成分分析（PCA）算法
weixin_39570530的博客
11-28 2090
一：引入问题首先看一个表格，下表是某些学生的语文，数学，物理，化学成绩统计：首先，假设这些科目成绩不相关，也就是说某一科目考多少分与其他科目没有关系，那么如何判断三个学生的优秀程度呢？首先我们一眼就能看出来，数学，物理，化学这三门课的成绩构成了这组数据的主成分（很显然，数学作为第一主成分，因为数据成绩拉的最开）。那么为什么我们能一眼看出来呢？当然是我们的坐标轴选对了！！下面，我们继续看一个表格，下...
PCA算法和实例
qq_27245709的博客
09-07 2005
本文转载自 瑟荻 http://blog.youkuaiyun.com/neal1991/article/details/46571999 ，仅用作学习。 PCA算法 算法步骤：  假设有m条n维数据。  1. 将原始数据按列组成n行m列矩阵X  2. 将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值  3. 求出协方差矩阵C=1/mXXT  4. 求出协方差矩阵
Day 44： 运用PCA的例子
weixin_50192514的博客
01-28 422
Python 回忆录2020/1/28Kaggle项目案例内容数据内容思路 2020/1/28 Kaggle项目 kaggel.com一个进行数据发掘和预测竞赛的在线平台. 国内还有一个天池网站（www.tianchi.aliyuncom）是一样的性质。未来可以在上面找项目做，拿名次。最重要的是可以用数据锻炼自己的思维能力。 这一次的小练习，也是在kaggel上找到的一个项目，目前还没有学习机器算法相关的知识，所以这次只是记录一下如何把数据进行预处理（运用一下PCA）。 案例内容 希望预测出来哪一些物品会
PCA降维算法（内含PCA可视化迷你案例+PCA人脸识别降维案例+PCA逆转降噪案例）
weixin_51589123的博客
10-08 4758
文章目录1、sklearn中的降维算法（1）PCA（2）SVD（3）思考2、重要参数n_components3、PCA中的SVD4、重要接口inverse_transform5、重要接口，参数和属性总结6、案例：PCA对手写数字数据集的降维 1、sklearn中的降维算法 PCA使用的信息量衡量指标，就是样本方差，又称可解释性方 差，方差越大，特征所带的信息量越多。 （1）PCA 我们希望能够找出一种办法来帮助我们衡量特征上所带的信息量，让我们在降维的过程中，能够即减少特征的数量，又保留大部分有效信息——
PCA原理讲解及举例（含图像分析具体代码实例）
Lyndsey的博客
05-20 5071
1. 数据降维 降维是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。在实际的生产和应用中，降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。 降维具有如下一些优点： 使得数据集更易使用。 降低算法的计算开销。 去除噪声。 使得结果容易理解。 降维的算法有很多，比如主成分分析(PCA)、奇异值分解(SVD)、因子分析(FA)、独立成分分析(ICA)。 本篇文章我们主要
特征工程：PCA主成分分析（实例）
m0_52118763的博客
01-04 3578
1.特征转换的介绍 样本特征只能从原始数据集中选择吗? 答案是否定的。 我们可以对原有特征进行组合，转化和提取获取新的特征。 其实生活中有很多这样的例子比如： 从三维空间到二维平面 ->用单个摄像头捕获数据时,就像把数据集压入一个二维空间:[x, y, z] ->[CI,C2] ->在特征转换中，一开始就不认为原始特征空间是最好的。 ->可能用更少的特征可以更好的描述数据。 下面介绍几个概念： 维度缩减:特征转换、特征选择与特征构建 特征选择仅限于从原始列中选择特征; 特征转换算法
PCA的数学原理
wxing2008666的专栏
06-28 6698
PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。网上关于PCA的文章有很多，但是大多数只描述了PCA的分析过程，而没有讲述其中的原理。这篇文章的目的是介绍PCA的基本数学原理，帮助读者了解PCA的工作机制是什么。 当然我并不打算把文章写成纯数
PCA主成分分析实例
yy031的博客
10-07 816
#主成分分析 import numpy as np ave_x=1.81 ave_y=1.91 dataAdjust_x=np.array([0.69,-1.31,0.39,0.09,1.29,0.49,0.19,-0.81,-0.31,-0.71]) dataAdjust_y=np.array([0.49,-1.21,0.99,0.29,1.09,0.79,-0.31,-0.81,-0.31,-1.01]) dataAdjust=np.vstack((dataAdjust_x,dataAdjust_y)
PCA算法的简单案例应用
最新发布
09-23
PCA算法在图像识别以及高维度数据降维处理中有很强的应用性，还可用于解析多元事物的主要影响因素、简化复杂问题等。以下结合引用内容介绍两个简单案例应用： - **人脸识别**：PCA可用于人脸识别。它能从多元事物中解析出主要影响因素，揭示事物本质，简化复杂问题，结合人脸识别实例，能利用其在降维和特征提取方面的有效性进行详细分析。通过计算特征值最大的特征向量对原始数据进行线性变换，可对人脸图像数据进行处理，比如将高维的人脸图像数据投影到较低维空间，从而实现特征提取和降维，有助于后续的识别工作 [^1][^2]。 - **高维度数据降维**：假设存在m条n维数据，PCA算法可按以下步骤对其降维。首先将原始数据按列组成n行m列矩阵X，接着将X的每一行进行零均值化（减去该行均值），之后求出协方差矩阵，再计算协方差矩阵的特征值及对应的特征向量，把特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P，最终得到降维到k维后的数据 [^3]。 ```python import numpy as np # 示例数据 X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]) # PCA算法步骤实现 # 1. 将原始数据按列组成n行m列矩阵X # 这里X已经是符合要求的矩阵 # 2. 将X的每一行进行零均值化 X_mean = np.mean(X, axis=0) X_centered = X - X_mean # 3. 求出协方差矩阵 cov_matrix = np.cov(X_centered, rowvar=False) # 4. 求出协方差矩阵的特征值及对应的特征向量 eigenvalues, eigenvectors = np.linalg.eig(cov_matrix) # 5. 将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P k = 2 # 降维到2维 idx = eigenvalues.argsort()[::-1] eigenvectors = eigenvectors[:, idx] P = eigenvectors[:, :k] # 6. 得到降维到k维后的数据 X_reduced = np.dot(X_centered, P) print("降维后的数据：") print(X_reduced) ```
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值