本文属于「数据库系统学习实践」系列文章之一,这一系列着重于「数据库系统知识的学习与实践」。由于文章内容随时可能发生更新变动,欢迎关注和收藏数据库系统系列文章汇总目录一文以作备忘。需要特别说明的是,为了透彻理解和全面掌握数据库系统,本系列文章中参考了诸多博客、教程、文档、书籍等资料,限于时间精力有限,这里无法一一列出。部分重要资料的不完全参考目录如下所示,在后续学习整理中还会逐渐补充:
- 数据库系统概念 第六版
Database System Concepts, Sixth Edition,作者是Abraham Silberschatz, Henry F. Korth, S. Sudarshan,机械工业出版社- 数据库系统概论 第五版,王珊 萨师煊编著,高等教育出版社
文章目录
本章学习关系数据理论(即关系规范化理论)。6.1节从数据库逻辑设计中如何构造一个好的数据库模式这一问题出发,阐明关系规范化理论研究的实际背景。6.2节介绍规范化理论,讨论各种范式及可能存在的插入、删除等问题,并直观描述解决方法。6.3节和6.4节进一步讨论关系数据理论,其中6.3节讨论函数依赖的推理规则,6.4节给出模式等价的不同定义及模式分解算法。6.1和6.2节是基本内容,本科学生需要掌握,6.3节和6.4节可作为研究生的学习内容。
本章参考文献

6.1 问题的提出
前面讨论了数据库系统的一般概念,介绍了关系数据库的基本概念、关系模型的三个部分以及关系数据库标准语言SQL。但还有一个很基本的问题尚未涉及:针对一个具体问题,应该如何构造一个适合于它的数据库模式——应构造几个关系模式、每个关系由哪些属性组成……?这是数据库设计的问题,准确地说是关系数据库逻辑设计的问题。
实际上,设计任何一种数据库应用系统,不论是层次的、网状的、关系的,都会遇到如何构造合适的数据模式即逻辑结构的问题。由于关系模式有严格的数学理论基础,并且可向别的数据模型转换,因此人们以关系模型为背景来讨论这个问题,形成了数据库逻辑设计的一个有力工具——关系数据库的规范化理论。特别地,规范化理论虽然以关系模型为背景,但它对于一般的数据库逻辑设计同样具有理论上的意义。
首先回顾一下关系模型的形式化定义——在第2章关系数据库中已经讲过,一个关系模式应当是一个五元组 R ( U , D , D O M , F ) R(U, D, DOM, F) R(U,D,DOM,F)
- 关系名 R R R 是符号化的元组语义;
- U U U 为一组属性;
- D D D 为属性组 U U U 中的属性所来自的域;
- D O M DOM DOM 为属性到域的映射;
- F F F 为属性组 U U U 上的一个数据依赖
由于 D , D O M D, DOM D,DOM 与模式设计关系不大,因此本章中把关系模式看作一个三元组: R ⟨ U , F ⟩ R\langle U, F\rangle R⟨U,F⟩ 当且仅当 U U U 上的一个关系 r r r 满足 F F F 时, r r r 称为关系模式 R ⟨ U , F ⟩ R\langle U, F\rangle R⟨U,F⟩ 的一个关系。
作为一个二维表,关系要符合一个最基本的条件——每个分量必须是不可分的数据项。满足了这个条件的关系模式就属于第一范式 1NF 。
在模式设计中,假设已知一个模式 S ϕ S_\phi Sϕ ,它仅由单个关系模式组成,问题是要设计一个模式 S D S_D SD ,它与 S ϕ S_\phi Sϕ 等价,但在某些指定的方面更好一些。这里通过一个例子说明,一个不好的模式会有哪些问题,分析它们产生的原因,并从中找到设计一个更好的关系模式的方法。
在举例之前,先非形式地讨论一下数据依赖的概念:数据依赖是一个关系内部、属性与属性之间的一种约束关系,这种约束关系是通过属性间值的相等与否体现出来的数据间的关联。它是现实世界属性间相互联系的抽象,是数据内在的性质,是语义的体现。人们已经提出了许多种类型的数据依赖,其中最重要的是函数依赖 functional dependency, FD 和多值依赖 multi-valued dependency, MVD(参考资料:Functional dependency in relational database theory、Multivalued dependency)。
函数依赖极为普遍地存在于现实生活中。比如描述一个学生的关系,可以有学号 Sno 、姓名 Sname 、系名 Sdept 等几个属性。由于一个学号只对应一个学生,一个学生只在一个系学习。因此当学号值确定之后,学生姓名、所在系的值也就被唯一地确定了。属性间的这种依赖关系,类似于数学中的函数
y
=
f
(
x
)
y = f(x)
y=f(x) ,自变量
x
x
x 确定以后,相应的函数值
y
y
y 也就唯一地确定了。类似地有 Sno 函数决定 Sname ,Sno 函数决定 Sdept ,记作
S
n
o
→
S
n
a
m
e
,
S
n
o
→
S
d
e
p
t
Sno \to Sname,\ Sno \to Sdept
Sno→Sname, Sno→Sdept 。
【例6.1】建立一个描述学校教务的数据库,该数据库涉及的对象包括学生的学号 Sno 、所在系 Sdept 、系主任姓名 Mname 、课程号 Cno 、成绩 Grade 。假设用一个单一的关系模式 Student 来表示,则该关系模式的属性集合为:
U
=
{
S
n
o
,
S
d
e
p
t
,
M
n
a
m
e
,
C
n
o
,
G
r
a
d
e
}
U = \{ Sno, Sdept, Mname, Cno, Grade\}
U={Sno,Sdept,Mname,Cno,Grade} 现实中的已知事实(语义)告诉我们:
① 一个系有若干学生,但一个学生只属于一个系;
② 一个系只有一名(正职)负责人;
③ 一个学生可以选修多门课程,每门课程有若干学生选修;
④ 每个学生学习每一门课程有一个成绩。
于是得到属性组
U
U
U 上的一组函数依赖
F
F
F(即图6.1):
F
=
{
S
n
o
→
S
d
e
p
t
,
S
d
e
p
t
→
M
n
a
m
e
,
(
S
n
o
,
C
n
o
)
→
G
r
a
d
e
}
F = \{ Sno \to Sdept, Sdept \to Mname, (Sno, Cno) \to Grade \}
F={Sno→Sdept,Sdept→Mname,(Sno,Cno)→Grade} 如果只考虑函数依赖这一种数据依赖,可以得到一个描述学生的关系模式
S
t
u
d
e
n
t
⟨
U
,
F
⟩
Student \langle U, F\rangle
Student⟨U,F⟩ 。表6.1是某一时刻关系模式 Student 的一个实例,即数据表: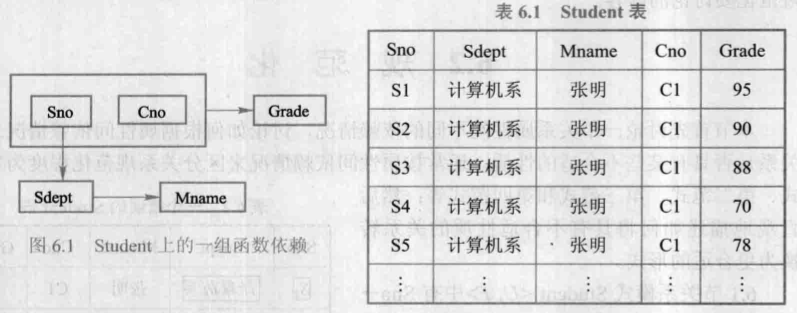
但是,这个关系模式存在以下问题,即不是一个好的模式:
- 数据冗余
比如,每个系的系主任姓名重复出现,重复次数与「该系所有学生的所有课程成绩」出现次数相同,这将浪费大量的存储空间。 - 更新异常
update anomalies
由于数据冗余,当更新数据库中的数据时,系统要付出很大代价来维护数据库的完整性,否则会面临数据不一致的危险。比如,某系更换系主任后,必须修改与该系学生有关的每个元组。 - 插入异常
insertion anomalies
如果一个系刚成立,尚无学生,则无法把这个系及其系主任的信息存入数据库。 - 删除异常
deletion anomalies
如果某个系的学生全部毕业了,则在删除该系学生信息的同时,这个系及其系主任的信息也丢掉了。
鉴于存在以上种种问题,可以得出这样的结论:Student 关系模式不是一个好的模式。一个好的模式应当不会发生插入异常、删除异常和更新异常,数据冗余应尽可能少。
为什么会发生这些问题呢?因为这个模式中的函数依赖存在某些不好的性质。这就是本章要讨论的问题。假如把这个单一的关系模式改造一下,分成三个关系模式:
S
(
S
n
o
,
S
d
e
p
t
,
S
n
o
→
S
d
e
p
t
)
;
S
C
(
S
n
o
,
C
n
o
,
(
S
n
o
,
C
n
o
)
→
G
r
a
d
e
)
;
D
E
P
T
(
S
d
e
p
t
,
M
n
a
m
e
,
S
d
e
p
t
→
M
n
a
m
e
)
\begin{aligned} &S(Sno, Sdept, Sno\to Sdept);\\ &SC(Sno, Cno, (Sno, Cno) \to Grade);\\ &DEPT(Sdept, Mname, Sdept\to Mname) \end{aligned}
S(Sno,Sdept,Sno→Sdept);SC(Sno,Cno,(Sno,Cno)→Grade);DEPT(Sdept,Mname,Sdept→Mname) 这三个模式都不会发生插入异常、删除异常的问题,数据冗余也得到了控制。
一个模式的数据依赖会有哪些不好的性质?如何改造一个不好的模式?这就是下节「规范化理论」要讨论的内容。
6.2 规范化
本节首先讨论一个关系的属性间的不同依赖情况,讨论如何根据属性间依赖情况、判定关系是否具有某些不合适的性质,通常按属性间依赖情况来区分关系规范化程度,分为第一范式、第二范式、第三范式和第四范式等;然后直观地描述如何将具有不合适性质的关系,转换为更合适的形式。
6.1节关系模式 S t u d e n t ⟨ U , F ⟩ Student\langle U, F\rangle Student⟨U,F⟩ 职工有 S n o → S d e p t Sno \to Sdept Sno→Sdept 成立,即在任何时刻 S t u d e n t Student Student 的关系实例(即 S t u d e n t Student Student 数据表)中,不可能存在两个元组在 S n o Sno Sno 上的值相等、而在 S d e p t Sdept Sdept 上的值不等。因此,下表的 S t u d e n t Student Student 表是错误的,因为表中有两个元组在 S n o Sno Sno 上都等于 S 1 S_1 S1 ,而在 S d e p t Sdept Sdept 上一个为计算机系、另一个为自动化系。
6.2.1 函数依赖
定义6.1 设 R ( U ) R(U) R(U) 是属性集 U U U 上的关系模式, X , Y X, Y X,Y 是 U U U 的子集。若对于 R ( U ) R(U) R(U) 的任意一个可能的关系 r r r , r r r 中不可能存在两个元组,在 X X X 上的属性值相等、而在 Y Y Y 上的属性值不等,则称 X X X 函数决定 Y Y Y 或 Y Y Y 函数依赖于 X X X ,记作 X → Y X\to Y X→Y 。
函数依赖和别的数据依赖一样,都是语义范畴的概念,只能根据语义来确定一个函数依赖。例如,姓名 → \to → 年龄这一函数依赖,只有在该部门没有同名人的条件下成立,如果有同名人,则年龄就不再函数依赖于姓名了。
设计者也可对现实世界作强制性规定,例如规定不允许同名人出现,因而使姓名 → \to → 年龄函数依赖成立。这样,当插入某个元组时,这个元组上的属性值必须满足规定的函数依赖,若发现同名人存在,则拒绝插入该元组(完整性约束条件)。
注意,函数依赖不是指关系模式 R R R 的某个或某些关系满足的约束条件,而是指 R R R 的一切关系均要满足的约束条件。下面介绍一些术语和记号。
- X → Y X \to Y X→Y ,但 Y ⊈ X Y \not \subseteq X Y⊆X ,则称 X → Y X\to Y X→Y 是非平凡的函数依赖;
- X → Y X \to Y X→Y ,但 Y ⊆ X Y \subseteq X Y⊆X ,则称 X → Y X\to Y X→Y 是平凡的函数依赖。对于任一关系模式,平凡函数依赖都是必然成立的,它不反映新的语义。若不特别声明,总是讨论非平凡的函数依赖。
-
X
→
Y
X \to Y
X→Y ,则
X
X
X 称为这个函数依赖的决定属性组,也称为决定因素
determinant。 - 若 X → Y , Y → X X \to Y,\ Y \to X X→Y, Y→X ,则记为 X ↔ Y X \lrarr Y X↔Y 。
- 若 Y Y Y 不函数依赖于 X X X ,则记为 X ↛ Y X \not \to Y X→Y 。
定义6.2 在
R
(
U
)
R(U)
R(U) 中,如果
X
→
Y
X \to Y
X→Y ,并且对于
X
X
X 的任何一个真子集
X
′
X'
X′ ,都有
X
′
↛
Y
X' \not \to Y
X′→Y ,则称
Y
Y
Y 对
X
X
X 完全函数依赖,记作
X
→
F
Y
X \stackrel{F} \to Y
X→FY 若
X
→
Y
X \to Y
X→Y ,但
Y
Y
Y 不完全函数依赖于
X
X
X ,则称
Y
Y
Y 对
X
X
X 部分函数依赖 partial functional dependency ,记作
X
→
P
Y
X \stackrel{P} \to Y
X→PY
【例6.1】中的 ( S n o , C n o ) → F G r a d e (Sno, Cno) \stackrel {F}\to Grade (Sno,Cno)→FGrade 是完全函数依赖, ( S n o , C n o ) → P S d e p t (Sno, Cno) \stackrel{P} \to Sdept (Sno,Cno)→PSdept 是部分函数依赖,因为 S n o → S d e p t Sno \to Sdept Sno→Sdept 成立,而 S n o Sno Sno 是 ( S n o , C n o ) (Sno, Cno) (Sno,Cno) 的真子集。
定义6.3 在
R
(
U
)
R(U)
R(U) 中,如果
X
→
Y
(
Y
⊈
X
)
,
Y
↛
X
,
Y
→
Z
(
Z
⊈
Y
)
X\to Y\ (Y \not \subseteq X),\ Y \not \to X,\ Y \to Z\ (Z \not \subseteq Y)
X→Y (Y⊆X), Y→X, Y→Z (Z⊆Y) 则称
Z
Z
Z 对
X
X
X 传递函数依赖 transitive functional dependency ,记为
X
→
T
Z
X\stackrel{T} \to Z
X→TZ 或者写为
X
→
传
递
Z
X\stackrel{传递} \to Z
X→传递Z(这里加上条件
Y
↛
X
Y\not \to X
Y→X ,是因为如果
Y
→
X
Y \to X
Y→X ,则
X
↔
Y
X\lrarr Y
X↔Y ,实际上是
X
→
直
接
Z
X \stackrel{直接} \to Z
X→直接Z ,是直接函数依赖而非传递函数依赖)。
【例6.1】中有 S n o → S d e p t , S d e p t → M n a m e Sno \to Sdept,\ Sdept \to Mname Sno→Sdept, Sdept→Mname 成立,所以 S n o → T M n a m e Sno \stackrel{T}\to Mname Sno→TMname 。
6.2.2 键(码)
定义6.4 设
K
K
K 是
R
⟨
U
,
F
⟩
R\langle U, F\rangle
R⟨U,F⟩ 中的属性或属性组合,若
K
→
F
U
K \stackrel {F} \to U
K→FU ,则
K
K
K 为
R
R
R 的候选键 candidate key 。
键是关系模式中的一个重要概念。在第2章已给出了关于键的若干定义,这里用函数依赖的概念重新定义键。注意,
U
U
U 是完全函数依赖于
K
K
K 、而非部分函数依赖于
K
K
K ,如果
U
U
U 部分函数依赖于
K
K
K ,即
K
→
P
U
K \stackrel{P} \to U
K→PU ,则
K
K
K 称为超键 super key 。候选键是最小的超键,即
K
K
K 的任意一个真子集都不是候选键。若候选键多于一个,则选定其中的一个作为主键 primary key 。
包含在任何一个候选键中的属性,称为主属性 prime attribute ;不包含在任何候选键中的属性,称为非主属性 nonprime attribute 或非键属性 non-key attribute 。最简单的情况,单个属性是键(在后面的章节中,主键或候选键都简称为键,可根据上下文加以识别);最极端的情况,整个属性组是键,称为全键 all-key 。
【例6.2】关系模式 S ( S n o ‾ , S d e p t , S a g e ) S(\underline{Sno}, Sdept, Sage) S(Sno,Sdept,Sage) 中单个属性 S n o Sno Sno 是键,用下划线标识出来。 S C ( S n o , C n o ‾ , G r a d e ) SC(\underline {Sno, Cno}, Grade) SC(Sno,Cno,Grade) 中属性组合 ( S n o , C n o ) (Sno, Cno) (Sno,Cno) 是键。
【例6.3】关系模式
R
(
P
,
W
,
A
)
R(P, W, A)
R(P,W,A) 中,属性
P
P
P 表示演奏者、
W
W
W 表示作品、
A
A
A 表示听众。假设一个演奏者可以演奏多个作品,某一作品可被多个演奏者演奏,听众也可以欣赏不同演奏者的不同作品,这个关系模式的键为
(
P
,
W
,
A
)
(P, W, A)
(P,W,A) ,即 all-key 。
定义6.5 关系模式
R
R
R 中属性或属性组
X
X
X 并非
R
R
R 的键,但
X
X
X 是另一个关系模式的键,则称
X
X
X 是
R
R
R 的外键 foreign key 。
如在 S C ( S n o , C n o ‾ , G r a d e ) SC(\underline {Sno, Cno}, Grade) SC(Sno,Cno,Grade) 中 S n o Sno Sno 不是键,但 S n o Sno Sno 是关系模式 S ( S n o ‾ , S d e p t , S a g e ) S(\underline{Sno}, Sdept, Sage) S(Sno,Sdept,Sage) 的键,则 S n o Sno Sno 是关系模式 S C SC SC 的外键。
主键与外键提供了一个表示关系间联系的手段,如【例6.2】中关系模式 S S S 与 S C SC SC 的联系,就是通过 S n o Sno Sno 来体现的。
6.2.3 范式
关系数据库中的关系是要满足一定要求的,满足不同程度要求的为不同范式。满足最低要求的叫第一范式,简称1NF;在第一范式中满足进一步要求的叫第二范式,简称2NF,其余以此类推。
有关范式理论的研究,主要是 E. F. Codd 做的工作。1971-1972年 Codd 系统地提出了1NF、2NF、3NF的概念,讨论了规范化的问题。1974年,Codd 和 Boyce 共同提出了一个新范式,即BCNF。1976年 Fagin 提出了4NF。后来又有研究者提出了5NF。
所谓「第几范式」原本是表示关系的某一种级别,所以常称某一关系模式 R R R 为第几范式。现在则把范式这个概念,理解成符合某一种级别的关系模式的集合,即 R R R 为第几范式就可以写成 R ∈ xNF R \in \textrm{xNF} R∈xNF 。
对于各种范式之间的关系,有:
5NF
⊂
4NF
⊂
BCNF
⊂
3NF
⊂
2NF
⊂
1NF
\textrm{5NF} \subset \textrm{4NF} \subset \textrm{BCNF} \subset \textrm{3NF} \subset \textrm{2NF} \subset \textrm{1NF}
5NF⊂4NF⊂BCNF⊂3NF⊂2NF⊂1NF 成立,如下图6.2所示:
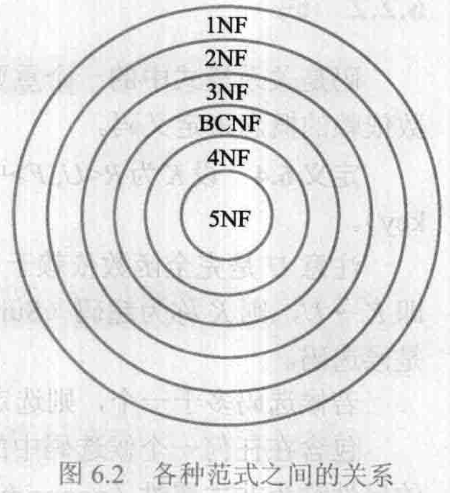
一个低一级范式的关系模式,通过模式分解 schema decomposition 可以转换为若干个高一级范式的关系模式的集合,这种过程就叫规范化 normalization 。
6.2.4 2NF
1NF很简单。关系模式作为一个二维表,只要符合一个最基本的条件——每个分量必须是不可分的数据项,就属于第一范式 1NF 。
定义6.6 若 R ∈ 1NF R \in \textrm{1NF} R∈1NF ,且每一个非主属性完全函数依赖于任何一个候选键,则 R ∈ 2NF R \in \textrm{2NF} R∈2NF 。
下面先举一个不是
2NF
\textrm{2NF}
2NF 的例子。
【例6.4】有关系模式
S
L
C
(
S
n
o
,
S
d
e
p
t
,
S
l
o
c
,
C
n
o
,
G
r
a
d
e
)
SLC(Sno, Sdept, Sloc, Cno, Grade)
SLC(Sno,Sdept,Sloc,Cno,Grade) ,其中
S
l
o
c
Sloc
Sloc 为学生的住处,并且每个系的学生住在同一个地方。
S
L
C
SLC
SLC 的键为
(
S
n
o
,
C
n
o
)
(Sno, Cno)
(Sno,Cno) ,则函数依赖有:
(
S
n
o
,
C
n
o
)
→
F
G
r
a
d
e
S
n
o
→
S
d
e
p
t
,
(
S
n
o
,
C
n
o
)
→
P
S
d
e
p
t
S
n
o
→
S
l
o
c
,
(
S
n
o
,
C
n
o
)
→
P
S
l
o
c
S
d
e
p
t
→
S
l
o
c
\begin{aligned} &(Sno, Cno) \stackrel{F} \to Grade \\ &Sno \to Sdept,\ (Sno, Cno) \stackrel {P} \to Sdept \\ &Sno \to Sloc,\ (Sno, Cno) \stackrel {P} \to Sloc \\ &Sdept \to Sloc \end{aligned}
(Sno,Cno)→FGradeSno→Sdept, (Sno,Cno)→PSdeptSno→Sloc, (Sno,Cno)→PSlocSdept→Sloc 函数依赖关系如图6.3所示,用虚线表示部分函数依赖:
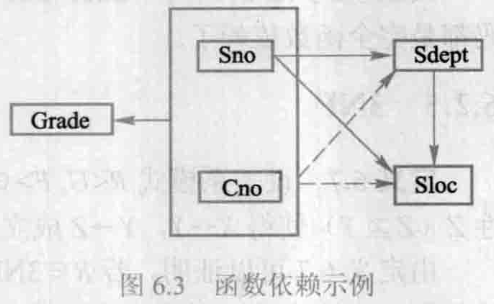
另外, S d e p t Sdept Sdept 还能函数决定 S l o c Sloc Sloc ,这一点在讨论第二范式时暂不考虑。可看到非主属性 S d e p t , S l o c Sdept,\ Sloc Sdept, Sloc 并不完全函数依赖于键,因此 S L C ( S n o , S d e p t , S l o c , C n o , G r a d e ) SLC(Sno, Sdept, Sloc, Cno, Grade) SLC(Sno,Sdept,Sloc,Cno,Grade) 不符合2NF定义,即 S L C ∉ 2NF SLC \notin \textrm{2NF} SLC∈/2NF 。
一个关系模式
R
R
R 不属于
2NF
\textrm{2NF}
2NF ,就会产生以下几个问题:
(1)插入异常。假若要插入一个学生
S
n
o
=
S
7
,
S
d
e
p
t
=
P
H
Y
,
S
l
o
c
=
B
L
D
2
Sno = S7,\ Sdept = PHY,\ Sloc = BLD2
Sno=S7, Sdept=PHY, Sloc=BLD2 ,但该生还未选课,即这个学生无
C
n
o
Cno
Cno ,这一元组就插入进
S
L
C
SLC
SLC 中。因为插入元组时必须给定键值,而此时键值的一部分为空,因而学生的固有信息就无法插入。
(2)删除异常。假定某个学生只选一门课,如
S
4
S4
S4 就选了一门课
C
3
C3
C3 ,现在
C
3
C3
C3 这门课他也不选了,那么
C
3
C3
C3 这个数据项就要删除。而
C
3
C3
C3 是主属性,删除了
C
3
C3
C3 ,整个元组就必须一起删除,使得
S
4
S4
S4 的其他信息也被删除了,从而造成删除异常,即不应删除的信息也删除了。
(3)修改复杂。某个学生从数学系
M
A
MA
MA 转到计算机科学系
C
S
CS
CS ,这本来只需修改此学生元组中的
S
d
e
p
t
Sdept
Sdept 分量即可,但因为关系模式
S
L
C
SLC
SLC 中还含有系的住处
S
l
o
c
Sloc
Sloc 属性、学生转系将同时改变住处,因而还必须修改元组中的
S
l
o
c
Sloc
Sloc 分量。
此外,如果这个学生选修了
k
k
k 门课程,则
S
d
e
p
t
,
S
l
o
c
Sdept,\ Sloc
Sdept, Sloc 就重复存储了
k
k
k 次,不仅存储冗余度大,而且必须无遗漏地修改
k
k
k 个元组中的全部
S
d
e
p
t
,
S
l
o
c
Sdept,\ Sloc
Sdept, Sloc 信息,造成修改的复杂化。
分析上面的例子可知,问题在于有两类非主属性,一类如
G
r
a
d
e
Grade
Grade ,它是完全函数依赖于键的;另一类如
S
d
e
p
t
,
S
l
o
c
Sdept,\ Sloc
Sdept, Sloc ,它们对键不是完全函数依赖。解决的方法是,用投影分解把关系模式
S
L
C
SLC
SLC 分解为两个关系模式:
S
C
(
S
n
o
,
C
n
o
‾
,
G
r
a
d
e
)
SC(\underline{Sno, Cno}, Grade)
SC(Sno,Cno,Grade) 和
S
L
(
S
n
o
‾
,
S
d
e
p
t
,
S
l
o
c
)
SL(\underline{Sno}, Sdept, Sloc)
SL(Sno,Sdept,Sloc) 。关系模式
S
C
,
S
L
SC,\ SL
SC, SL 属性间的函数依赖,可分别用图6.4、图6.5表示如下:
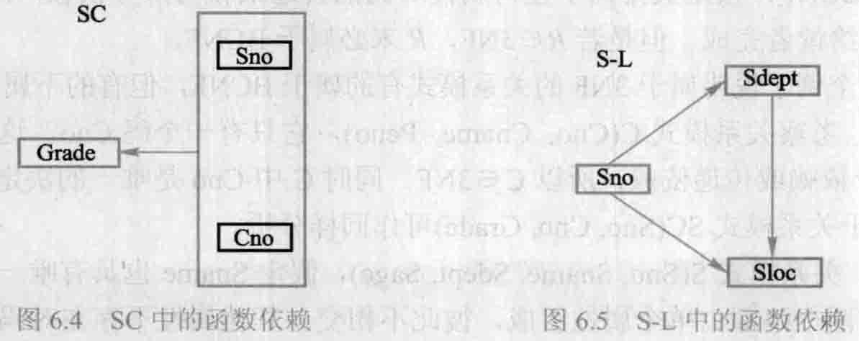
关系模式
S
C
SC
SC 的键为
(
S
n
o
,
C
n
o
)
(Sno, Cno)
(Sno,Cno) ,关系模式
S
L
SL
SL 的键为
S
n
o
Sno
Sno ,这样就使非主属性对键都是完全函数依赖了。
6.2.5 3NF
定义6.7 设关系模式 R ⟨ U , F ⟩ ∈ 1NF R\langle U, F\rangle \in \textrm{1NF} R⟨U,F⟩∈1NF ,若 R R R 中不存在这样的键 X X X ,属性(组) Y Y Y 及非主属性(组) Z ( Y ⊈ Z ) Z\ (Y \not \subseteq Z) Z (Y⊆Z) ,使得 X → Y , Y → Z X \to Y,\ Y \to Z X→Y, Y→Z 成立, Y ↛ X Y \not \to X Y→X ,则称 R ⟨ U , F ⟩ ∈ 3NF R\langle U, F\rangle \in \textrm{3NF} R⟨U,F⟩∈3NF 。
由定义6.7可证明,若 R ∈ 3NF R \in \textrm{3NF} R∈3NF ,则每个非主属性既不传递依赖于键,也不部分依赖于键。即,可以证明如果 R R R 属于 3NF \textrm{3NF} 3NF ,则必有 R R R 属于 2 N F 2NF 2NF 。
在图6.4中关系模式 S C SC SC 没有传递依赖,而图6.5中关系模式 S L SL SL 存在非主属性对键的传递依赖——在 S L SL SL 中,由 S n o → S d e p t ( S d e p t ↛ S n o ) , S d e p t → S l o c Sno \to Sdept\ (Sdept \not \to Sno),\ Sdept \to Sloc Sno→Sdept (Sdept→Sno), Sdept→Sloc ,可得 S n o → T S l o c Sno \stackrel {T}\to Sloc Sno→TSloc ,因此 S C ∈ 3NF , S L ∉ 3NF SC \in \textrm{ 3NF},\ SL \notin \textrm{3NF} SC∈ 3NF, SL∈/3NF 。
一个关系模式 R R R 若不是 3NF \textrm{3NF} 3NF ,就会产生与6.2.4节中 2NF \textrm{2NF} 2NF 相类似的问题,可类比 2NF \textrm{2NF} 2NF 的反义加以说明。解决的办法同样是将 S L SL SL 分解为: S D ( S n o , S d e p t ) SD(Sno, Sdept) SD(Sno,Sdept) 和 D L ( S d e p t , S l o c ) DL(Sdept, Sloc) DL(Sdept,Sloc) 。分解后的关系模式 S D , D L SD,\ DL SD, DL 中不再存在传递依赖。
6.2.6 BCNF
BCNF (Boyce Codd Normal Form) 是由 Boyce 与 Codd 提出的,比上述的
3NF
\textrm{3NF}
3NF 又进了一步,通常认为
BCNF
\textrm{BCNF}
BCNF 是修改的第三范式,有时也称为扩充的第三范式。
定义6.8 关系模式 R ⟨ U , F ⟩ ∈ 1NF R\langle U, F\rangle \in \textrm{1NF} R⟨U,F⟩∈1NF ,若 X → Y X \to Y X→Y 且 Y ⊈ X Y\not \subseteq X Y⊆X 时 X X X 必含有键,则 R ⟨ U , F ⟩ ∈ BCNF R\langle U, F\rangle \in \textrm{BCNF} R⟨U,F⟩∈BCNF 。
也就是说,关系模式 R ⟨ U , F ⟩ R\langle U, F\rangle R⟨U,F⟩ 中,若每个决定因素都包含键,则 R ⟨ U , F ⟩ ∈ BCNF R\langle U, F\rangle \in \textrm{BCNF} R⟨U,F⟩∈BCNF 。更简单一点说,所有非平凡函数依赖的左部都必须包含候选键,即具有函数依赖集合 F F F 的关系模式 R R R 属于 BCNF \textrm{BCNF} BCNF 的条件是,任何函数依赖 X → Y X \to Y X→Y 都是非平凡函数依赖、且 X X X 是 R R R 的一个超键。
由 BCNF \textrm{BCNF} BCNF 的定义可以得到结论,一个满足 BCNF \textrm{BCNF} BCNF 的关系模式有以下性质:
- 所有非主属性,对每个键都是完全函数依赖,既不部分依赖于键,也不传递依赖于键(即满足 3NF \textrm{3NF} 3NF );
- 所有主属性,对每个不包含它的键,也是完全函数依赖,既不部分依赖,也不传递依赖;
- 没有任何属性,完全函数依赖于非键的任何一组属性
由于 R ∈ BCNF R \in \textrm{BCNF} R∈BCNF ,按定义排除了任何属性对键的传递依赖及部分依赖,所以 R ∈ 3NF R \in \textrm{3NF} R∈3NF 。只是若 R ∈ 3NF R \in \textrm{3NF} R∈3NF , R R R 未必属于 BCNF \textrm{BCNF} BCNF 。下面用几个例子说明,属于 3NF \textrm{3NF} 3NF 的关系模式有的属于 BCNF \textrm{BCNF} BCNF ,有的不属于 BCNF \textrm{BCNF} BCNF 。
【例6.5】考察关系模式 C ( C n o , C n a m e , P c n o ) C(Cno, Cname, Pcno) C(Cno,Cname,Pcno) ,它只有一个键 C n o Cno Cno ,这里没有任何属性对 C n o Cno Cno 部分或传递依赖,所以 C ∈ 3NF C \in \textrm{3NF} C∈3NF ,同时 C C C 中 C n o Cno Cno 也是唯一的决定因素,所以 C ∈ BCNF C \in \textrm{BCNF} C∈BCNF 。对于关系模式 S C ( S n o , C n o , G r a d e ) SC(Sno, Cno, Grade) SC(Sno,Cno,Grade) 可做同样分析。
【例6.6】关系模式 S ( S n o , S n a m e , S d e p t , S a g e ) S(Sno, Sname, Sdept, Sage) S(Sno,Sname,Sdept,Sage) ,假定 S n a m e Sname Sname 具有唯一性,那么 S S S 就有两个键,这两个键都由单个属性组成,彼此不相交,其他属性不存在对键的传递依赖与部分依赖,所以 S ∈ 3NF S \in \textrm{3NF} S∈3NF 。同时 S S S 中除 S n o , S n a m e Sno, Sname Sno,Sname 外没有其他决定因素,所以 S S S 也属于 BCNF \textrm{BCNF} BCNF 。
下面再举几个例子。
【例6.7】关系模式
S
J
P
(
S
,
J
,
P
)
SJP(S, J, P)
SJP(S,J,P) 中,
S
S
S 是学生、
J
J
J 表示课程、
P
P
P 表示名次。每个学生选修每门课程的成绩有一定的名次,每门课程中每一名次只有一名学生(即没有并列名次)。由语义可得下面的函数依赖:
(
S
,
J
)
→
P
;
(
J
,
P
)
→
S
(S, J) \to P;\ (J, P) \to S
(S,J)→P; (J,P)→S 所以
(
S
,
J
)
(S, J)
(S,J) 和
(
J
,
P
)
(J, P)
(J,P) 都可作为候选键,这两个键各由两个属性组成,而且它们是相交的。这一关系模式中,显然没有属性对键传递依赖或部分依赖。所以
S
J
P
∈
3NF
SJP \in \textrm{3NF}
SJP∈3NF ,而且除
(
S
,
J
)
(S, J)
(S,J) 与
(
J
,
P
)
(J, P)
(J,P) 以外没有其他决定因素,所以
S
J
P
∈
BCNF
SJP \in \textrm{BCNF}
SJP∈BCNF 。
【例6.8】关系模式
S
T
J
(
S
,
T
,
J
)
STJ(S, T, J)
STJ(S,T,J) 中,
S
S
S 是学生、
T
T
T 是教师、
J
J
J 是课程。每一教师只教一门课,每门课有若干教师,某一学生选定某门课,就对应一个固定的教师。由语义可得到如下的函数依赖。
(
S
,
J
)
→
T
;
(
S
,
T
)
→
J
;
T
→
J
(S, J) \to T; \ (S, T) \to J;\ T \to J
(S,J)→T; (S,T)→J; T→J 函数依赖关系如下图所示,这里
(
S
,
J
)
,
(
S
,
T
)
(S, J),\ (S, T)
(S,J), (S,T) 都是候选键:
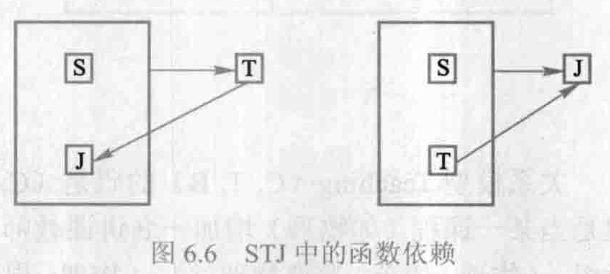
显然, S T J STJ STJ 是 3NF \textrm{3NF} 3NF ,因为没有任何非主属性对键传递依赖或部分依赖,但 S T J STJ STJ 不是 BCNF \textrm{BCNF} BCNF 关系,因为 T T T 是决定因素,而 T T T 不包含键。
对于不是 BCNF \textrm{BCNF} BCNF 的关系模式,仍然存在不合适的地方,可自己举例指出 S T J STJ STJ 的不合适之处。非 BCNF \textrm{BCNF} BCNF 的关系模式,也可以通过分解成为 BCNF \textrm{BCNF} BCNF 。例如 S T J STJ STJ 可分解为 S T ( S , T ) ST(S, T) ST(S,T) 与 T J ( T , J ) TJ(T,J) TJ(T,J) ,它们都是 BCNF \textrm{BCNF} BCNF 。
3NF \textrm{3NF} 3NF 和 BCNF \textrm{BCNF} BCNF 是在函数依赖的条件下,对模式分解所能达到的分离程度的测度。一个模式中的关系模式如果都属于 BCNF \textrm{BCNF} BCNF ,那么在函数依赖范畴内,它已实现了彻底的分离,已消除了插入和删除的异常。 3NF \textrm{3NF} 3NF 的不彻底性,表现在「可能存在主属性对键的部分依赖和传递依赖」上。
6.2.7 多值依赖
以上完全是在函数依赖的范畴内讨论问题。属于 BCNF \textrm{BCNF} BCNF 的关系模式是否就很完美了呢?下面来看一个例子。
【例6.9】学校中某一门课程由多个教师讲授,他们使用相同的一套参考书。每个教师可以讲授多门课程,每种参考书可以供多门课程使用。可用一个非规范化的关系来表示教师
T
T
T 、课程
C
C
C 、参考书
B
B
B 之间的关系,如表6.3所示。把这张表变成一张规范化的二维表,如表6.4所示。
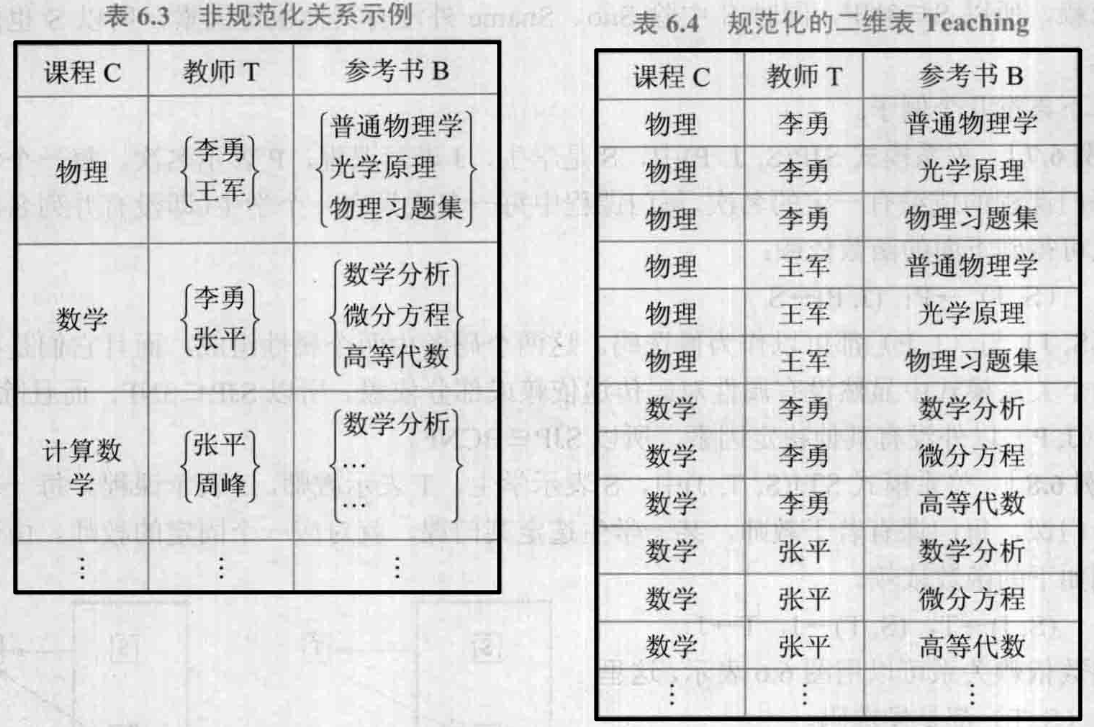
关系模型
T
e
a
c
h
i
n
g
(
C
,
T
,
B
)
Teaching(C, T, B)
Teaching(C,T,B) 的键是
(
C
,
T
,
B
)
(C, T, B)
(C,T,B) ,即全键 all-key ,因而
T
e
a
c
h
i
n
g
∈
BCNF
Teaching \in \textrm{BCNF}
Teaching∈BCNF 。但是当某一课程(如物理)增加一名讲课教师(如周英)时,必须插入多个(这里是三个)元组——(物理, 周英, 普通物理学), (物理, 周英, 光学原理), (物理, 周英, 物理习题集) 。
同样,某一门课(如数学)要去掉一本参考书(如微分方程),则必须删除多个(这里是两个)元组——(数学, 李勇, 微分方程), (数学, 张平, 微分方程) 。
因而,对数据的增删改很不方便,数据的冗余十分明显!!!仔细考察这类关系模式,发现它具有一种称为多值依赖 Multi-Valued Dependency, MVD 的数据依赖。
定义6.9 设 R ( U ) R(U) R(U) 是属性集 U U U 上的一个关系模式, X , Y , Z X, Y, Z X,Y,Z 是 U U U 的子集,并且 Z = U − X − Y Z = U - X - Y Z=U−X−Y 。关系模式 R ( U ) R(U) R(U) 中多值依赖 X → → Y X \to \to Y X→→Y 成立,当且仅当对 R ( U ) R(U) R(U) 的任一关系 r r r ,给定了一对 ( x , z ) (x, z) (x,z) 值,就有一组 Y Y Y 的值,这组值仅仅决定于 x x x 值而与 z z z 值无关。
例如,在关系模式
T
e
a
c
h
i
n
g
Teaching
Teaching 中,对于一个 (物理, 光学原理) 有一组
T
T
T 值 {李勇, 王军} ,这组值仅仅取决于课程
C
C
C 上的值 (物理) 。也就是说,对于另一个 (物理, 普通物理学) ,它对应的一组
T
T
T 值仍是 {李勇, 王军} ,尽管这时参考书
B
B
B 的值已经改变了。因此
T
T
T 多只依赖于
C
C
C ,即
C
→
→
T
C \to \to T
C→→T 。
对于多值依赖的另一个等价的形式化定义是:在 R ( U ) R(U) R(U) 的任一关系 r r r 中,如果存在元组 t , s t, s t,s 使得 t [ X ] = s [ X ] t[X] = s[X] t[X]=s[X] ,那么就必然存在元组 w , v ∈ r w, v \in r w,v∈r( w , v w, v w,v 可与 s , t s, t s,t 相同),使得 w [ X ] = v [ X ] = t [ X ] w[X] = v[X] = t[X] w[X]=v[X]=t[X] ,而 w [ Y ] = t [ Y ] , w [ Z ] = s [ Z ] , v [ Y ] = s [ Y ] , v [ Z ] = t [ Z ] w[Y] = t[Y],\ w[Z] = s[Z],\ v[Y] = s[Y],\ v[Z] = t[Z] w[Y]=t[Y], w[Z]=s[Z], v[Y]=s[Y], v[Z]=t[Z](即交换 s , t s, t s,t 元组的 Y Y Y 值所得的两个新元组,必定在 r r r 中),则 Y Y Y 多值依赖于 X X X ,记为 X → → Y X \to \to Y X→→Y 。这里, X , Y X, Y X,Y 是 U U U 的子集, Z = U − X − Y Z = U - X - Y Z=U−X−Y 。(?)
若 X → → Y X \to \to Y X→→Y ,而 Z = ∅ Z = \varnothing Z=∅ ,则称 X → → Y X \to \to Y X→→Y 为平凡的多值依赖。即对于 R ( X , Y ) R(X, Y) R(X,Y) ,如果有 X → → Y X \to \to Y X→→Y 成立,则 X → → Y X \to \to Y X→→Y 为平凡的多值依赖。
下面再举一个具有多值依赖的关系模式的例子。
【例6.10】关系模式
W
S
C
(
W
,
S
,
C
)
WSC(W, S, C)
WSC(W,S,C) 中,
W
W
W 表示仓库、
S
S
S 表示保管员、
C
C
C 表示商品。假设每个仓库有若干个保管员、有若干种商品。每个保管员保管所在仓库的所有商品,每种商品被所有保管员保管。列出关系如表6.5所示。
按照语义对于 W W W 的每一个值 W i W_i Wi , S S S 有一个完整的集合与之对应、而不论 C C C 取何值。所以 W → → S W \to \to S W→→S 。
如果用图6.7来表示这种对应,则对于 W W W 的某一个值 W i W_i Wi 的全部 S S S 值记作 { S } w i \{ S \}_{wi} {S}wi(表示在此仓库工作的全部保管员),全部 C C C 值记作 { C } w i \{ C\}_{wi} {C}wi(表示在此仓库存放的所有商品)。应当有 { S } w i \{ S\}_{wi} {S}wi 的每一个值和 { C } w i \{ C\}_{wi} {C}wi 中的每一个 C C C 值对应。于是
6.2.8 4NF
可用投影分解的方法,消去非平凡且非函数依赖的多值依赖,例如可把 W S C WSC WSC 分解为 W S ( W , S ) , W C ( W , C ) WS(W, S),\ WC(W, C) WS(W,S), WC(W,C) 。在 W S WS WS 中虽然有 W → → S W \to \to S W→→S ,但这是平凡的多值依赖。 W S WS WS 中已不存在非平凡、非函数依赖的多值依赖,所以 W S ∈ 4 N F WS \in 4NF WS∈4NF ,同理 W C ∈ 4 N F WC \in 4NF WC∈4NF 。
函数依赖和多值依赖,是两种最重要的数据依赖。如果只考虑函数依赖,则属于 BCNF \textrm{BCNF} BCNF 的关系模式规范化程度,已经是最高的了;如果考虑多值依赖,则属于 4 N F 4NF 4NF 的关系模式规范化程度,才是最高的。事实上,数据依赖中除函数依赖和多值依赖之外,还有其他数据依赖。
例如有一种连接依赖,函数依赖是多值依赖的一种特殊情况,而多值依赖实际上又是连接依赖的一种特殊情况,但连接依赖不像函数依赖和多值依赖可由语义直接导出,而是在关系的连接运算时才反映出来。存在连接依赖的关系模式,仍可能遇到数据冗余及插入、修改、删除异常等问题。如果消除了属于 4 N F 4NF 4NF 的关系模式中存在的连接依赖,则可进一步达到 5 N F 5NF 5NF 的关系模式。这里不再讨论连接依赖和 5 N F 5NF 5NF ,有兴趣的读者可参阅有关书籍。
6.2.9 规范化小结
在关系数据库中,对关系模式的基本要求是满足第一范式,这样的关系模式就是合法的、允许的。但是,人们发现有些关系模式存在插入、删除异常,以及修改复杂、数据冗余等问题,需要寻求解决这些问题的方法,这就是规范化的目的。
规范化的基本思想,是逐步消除数据依赖中不合适的部分,使模式中的各关系模式达到某种程度的分离,即 「一事一地」的模式设计原则。让一个关系描述一个概念、一个实体或者实体间的一种联系。若多于一个概念,就把它分离出去。因此,所谓规范化实质上就是概念的单一化。
人们认识这个原则是经历了一个过程的,从认识非主属性的部分函数依赖的危害开始,
2
N
F
,
3
N
F
,
B
C
N
F
,
4
N
F
2NF,\ 3NF,\ BCNF,\ 4NF
2NF, 3NF, BCNF, 4NF 的相继提出,是这个认识过程逐步深化的标志。图6.8可以概括这个过程:

关系模式的规范化过程,就是通过对关系模式的分解来实现的,即把低一级的关系模式分解为若干个高一级的关系模式。这种分解不是唯一的。下面将进一步讨论分解后的关系模式与原关系模式「等价」的问题,以及分解的算法。
6.3 数据依赖的公理系统
数据依赖的公理系统,是模式分解算法的理论基础。下面首先讨论函数依赖的一个有效而完备的公理系统——Armstrong公理系统。
定义6.11 对于满足一组函数依赖 F F F 的关系模式 R ⟨ U , F ⟩ R\langle U, F\rangle R⟨U,F⟩ ,其任何一个关系 r r r ,若函数依赖 X → Y X \to Y X→Y 都成立(即 r r r 中任意两元组 t , s t, s t,s ,若 t [ X ] = s [ X ] t[X] = s[X] t[X]=s[X] ,则 t [ Y ] = s [ Y ] t[Y] = s[Y] t[Y]=s[Y] ,即两元组在 X X X 属性上的值相等,就一定有两元组在 Y Y Y 属性上的值相等),则称 F F F 逻辑蕴涵 X → Y X \to Y X→Y 。
为了求得给定关系模式的键,为了从一组函数依赖求得蕴涵的函数依赖,例如已知函数依赖集合
F
F
F ,要问
X
→
Y
X \to Y
X→Y 是否为
F
F
F 所蕴涵,就需要一套推理规则。下面这组推理规则是1974年首先由 Armstrong 提出来的。
Armstrong公理系统 Armstrong's axiom 设
U
U
U 为属性集总体,
F
F
F 是
U
U
U 上的一组函数依赖,于是有关系模式
R
⟨
U
,
F
⟩
R\langle U, F\rangle
R⟨U,F⟩ ,对
R
⟨
U
,
F
⟩
R\langle U, F\rangle
R⟨U,F⟩ 来说有以下的推理规则:
- A1 自反律
reflexivity rule:若 Y ⊆ X ⊆ U Y \subseteq X\subseteq U Y⊆X⊆U ,则 X → Y X \to Y X→Y 为 F F F 所蕴涵; - A2 增广律
augmentation rule:若 X → Y X \to Y X→Y 为 F F F 所蕴涵,且 Z ⊆ U Z \subseteq U Z⊆U ,则 X Z → Y Z XZ \to YZ XZ→YZ 为 F F F 所蕴涵(此处的 X Z XZ XZ 代表 X ∪ Z X \cup Z X∪Z , Y Z YZ YZ 代表 Y ∪ Z Y \cup Z Y∪Z) - A3 传递律
transitivity rule:若 X → Y X \to Y X→Y 及 Y → Z Y \to Z Y→Z 为 F F F 所蕴涵,则 X → Z X \to Z X→Z 为 F F F 所蕴涵。
注意,由自反律所得到的函数依赖均是平凡的函数依赖,自反律的使用并不依赖于 F F F 。
定理6.1 Armstrong推理规则是正确的。
证明 下面从定义出发,证明推理规则的正确性。
(1)
(2)
(3)
根据A1、A2、A3这三条推理规则,可得到下面三条很有用的推理规则:
- 合并规则
union rule:由 X → Y , X → Z X\to Y,\ X \to Z X→Y, X→Z ,则 X → Y Z X \to YZ X→YZ ; - 伪传递规则
pseudo transitivity rule:由 X → Y , W Y → Z , X \to Y,\ WY\to Z, X→Y, WY→Z, ,有 X W → Z XW \to Z XW→Z ; - 分解规则
decomposition rule:由 X → Y X\to Y X→Y 及 Z ⊆ Y Z \subseteq Y Z⊆Y ,有 X → Z X \to Z X→Z 。
根据合并规则和分解规则,很容易得到这样一个重要事实:
引理6.1
X
→
A
1
A
2
…
A
k
X \to A_1 A_2 \dots A_k
X→A1A2…Ak 成立,当且仅当
X
→
A
i
X \to A_i
X→Ai 成立(
i
=
1
,
2
,
…
,
k
i = 1, 2, \dots, k
i=1,2,…,k)。
定义6.12 在关系模式
R
⟨
U
,
F
⟩
R\langle U, F\rangle
R⟨U,F⟩ 中为
F
F
F 所逻辑蕴涵的函数依赖的全体,叫做
F
F
F 的闭包 closure ,记为
F
+
F^+
F+ 。
人们把自反律、增广律、传递律称为Armstrong公理系统。Armstrong公理系统是有效的、完备的。Armstrong公理的 有效性 指的是:由 F F F 出发,根据Armstrong公理推导出来的每个函数依赖,一定在 F + F^+ F+ 中;完备性指的是: F + F^+ F+ 中的每个函数依赖,必定可以由 F F F 出发根据Armstrong公理推导出来。





 本文深入探讨数据库系统的规范化理论,包括函数依赖、键、范式等概念,阐述了2NF、3NF、BCNF的定义与问题,强调了消除数据冗余和异常的重要性,并介绍了模式分解在规范化过程中的作用。通过实例解析,帮助读者理解如何通过模式分解达到更高的规范化程度,以优化数据库设计。
本文深入探讨数据库系统的规范化理论,包括函数依赖、键、范式等概念,阐述了2NF、3NF、BCNF的定义与问题,强调了消除数据冗余和异常的重要性,并介绍了模式分解在规范化过程中的作用。通过实例解析,帮助读者理解如何通过模式分解达到更高的规范化程度,以优化数据库设计。

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










