深度学习之过拟合

什么是过拟合

举一个简单的例子：我们设计了一个模型来判断 一件物品是否为树叶。喂养这个模型的数据集中含有几张带有尖刺边缘的树叶。模型的设计者希望模型能满足每一个训练数据，模型就将尖刺边缘也纳入了参数中。当我们测试这个模型的泛化性能时，就会发现效果很差，因为模型钻牛角尖，它认为树叶必须带有尖刺边缘，所以它排除了所有没有带有尖刺边缘的树叶，但事实上，我们知道树叶并不一定带有尖刺边缘。结果为什么会这样？因为模型设计者的强迫症使得这个模型过分贴合整个训练集，结果把噪音点也拟合上了。

过拟合(overfitting)：模型过于复杂，在训练集上面的拟合效果非常好甚至可以达到损失为0，但是在测试集的拟合效果很不好

欠拟合(underfitting)： 模型过于简单 在训练集和测试集的拟合的效果都不好

欠拟合与过拟合

我们以“波士顿房价预测”为例，来从图像的角度直观感受一下什么叫过拟合，顺便也介绍一下欠拟合：

例子1：线性回归（房价预测）

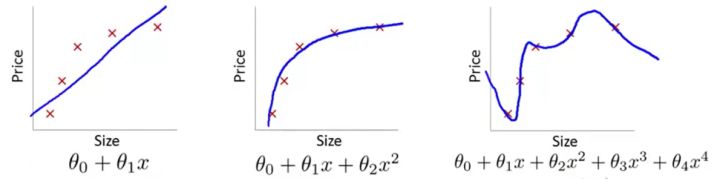
Fig.1 Linear regression（截屏自吴恩达机器学习）

我们看到第一张图的模型过于简单，而且损失函数的收敛速度很慢。这就使得优化算法做得再好，我们的模型的泛化性能也会很差，因为这条直线在训练集上的cost就很大，我们把这种训练集上的偏差很大的情况叫做欠拟合（Underfitting），也有一种历史叫法：高偏差（High bias）。

第二张图是我们合理假设的一个模型。可以看到，选取了合理的模型后，图像大致穿过了样本点。像极了做物理实验时，最后用一条曲线大致地穿过既定的样本点；和第一张图比起来，至少损失值大大下降了。

第三张图引入了高次项，就题论题来说，这太复杂了。虽然事实上对于是任意n个点，总能找到n+1次曲线方程将这n个点全部穿过，但是从模型的角度来讲，这显然不是好模型（姑且不说要用一个高次模型去拟合离散点要迭代多少次，学习率要调到多低）。即使它一板一眼地穿过了所有样本点，但谁能保证这种奇形怪状的曲线能穿过下一个随机给出的样本点呢？我们把这种和预测值和样本标签值几乎完全一致的情况叫做过拟合（Overfitting），历史上也称为高方差（High variance）。

 所以过拟合就是损失函数极小但泛化性能差的情况。落实在分类问题上就是训练集的损失函数值很小，但是验证集/测试集上的损失函数值很大

解决过拟合

我们一般有两种方法来减小过拟合的影响：

1.减少属性值（特征值）的数量。

• 人工选择哪些特征需要保留。
• 使用模型选择算法。

2.实行正则化

• 保留所有特征值，但是减小参数θ_j的值或数量级。
• 当我们有许多特征时，效果较好。其中每一个特征值都会对y造成影响

抑制过拟合的方法

 1增加训练的样本数量

2在损失函数上面添加正则项

3改变数据生成模型的噪声生成的方差