CNN中的卷积的理解

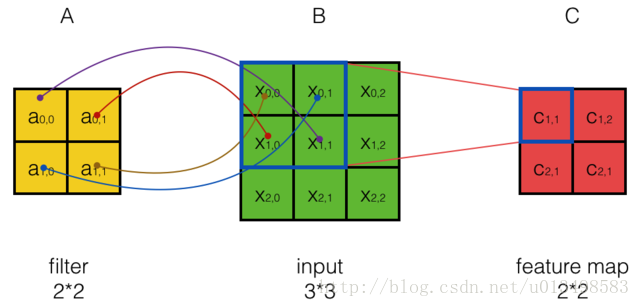
1、什么是卷积：图像中不同数据窗口的数据和卷积核（一个滤波矩阵）作内积的操作叫做卷积。其计算过程又称为滤波（filter)，本质是提取图像不同频段的特征。

其实CNN中的卷积并不是真正的卷积运算，而是一种互相关(cross-correlation)运算

卷积（convolution）：

S=f(t)*g(t-i)

互相关(cross-correlation)：

S=f(t)*g(t+i)

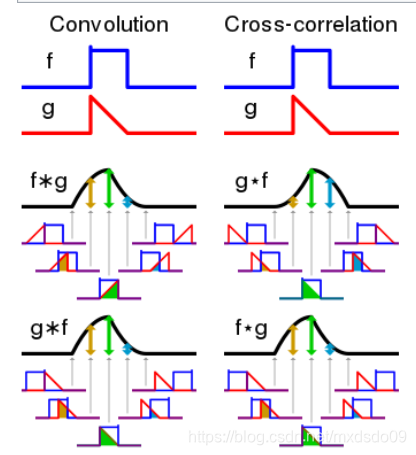
从图中很明显看出来，Convolution相当于把函数g反转180度在与f函数运算；而Cross-correlation相比卷积则少了那个反转，相当于直接进行矩阵相乘。

 

2、什么是卷积核：也称为滤波器filter，带着一组固定权重的神经元，通常是n*m二维的矩阵，n和m也是神经元的感受野（相当于对图像取的窗口大小，比如一次从128*128的输入图像中只取3*3的一个小窗口进行分析）。n*m 矩阵中存的是对感受野中数据处理的系数（W权重）。filter_size是指filter的大小，例如3*3； filter_num是指每种filter_size的filter个数，通常是通道个数

feature map(特征映射)：原始图像数据通过卷积核处理可以用来提取特定的特征（例如可以提取物体轮廓、颜色深浅等表现物体信息的特征）。通过卷积层从原始数据中提取出特征的过程又成为feature map(特征映射)。即每个卷积核只能提取一种相应的特征，每个卷积核对应一个特征映射，也就是feature map。

3、什么是卷积层：多个滤波器叠加便成了卷积层。

4、一个卷基层有多少个参数：一个卷积核使用一套权值以便”扫视’数据每一处时以同样的方式抽取特征，最终得到的是一种特征。 在tensorflow定义conv2d时需要指定卷积核的尺寸，本人现在的理解是一个卷积层的多个卷积核使用相同的m*n, 只是权重不同。 则一个卷积层的参数总共m*n*filter_num个，比全连接少了很多。

5、通道(chennel）怎么理解：一般为RGB三通道

6、几个参数:

a. 深度depth：卷积核个数，决定输出的depth厚度，卷积核尺寸决定输出长宽。

output（输出像素）= (input输入像素 - F卷积核长宽尺寸 + 2*P填充值)/stride卷积核每次移动的步长 +1

比如（7-3）/2 +1=3 ，所以下文中输出为3*3矩阵

b. 步长stride：决定移动多少步可以到边缘。

c. 填充值zero-padding：在外围边缘补充若干圈0，方便从初始位置以步长为单位可以刚好滑倒末尾位置，通俗地讲就是为了总长能被步长整除。 

 

 

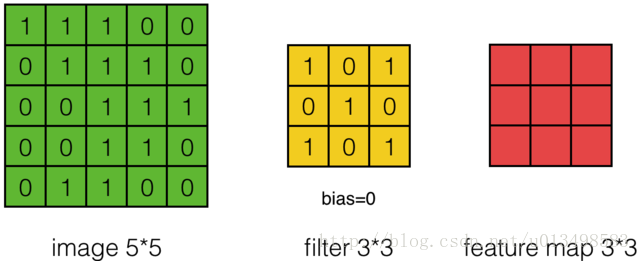
7、计算例子：

解析：图中input 7*7*3中，7*7代表图像的像素/长宽，3代表R、G、B 三个颜色通道，可以看到周边有填充0； 有两个3*3*3的卷积核Filter w0、Filter w1（3*3代表取的窗口长度*宽度，后面一个*3代表通道个数，RGB三个通道）,每个filter对应每个通道有一组3*3的w权重；一个filter滑动到一个位置后计算三个通道的卷积，求和，加bias，得到这个filter在该位置的最终结果；每个卷积核的输出是各个通道的汇总；输出的个数与filter矩阵维数相同。两个卷积核，最后的output为3*3*2，其depth=2。窗口每次移动两个步长取3*3的局部数据，即stride=2。外围填0部分为一位，所以zero-padding=1。

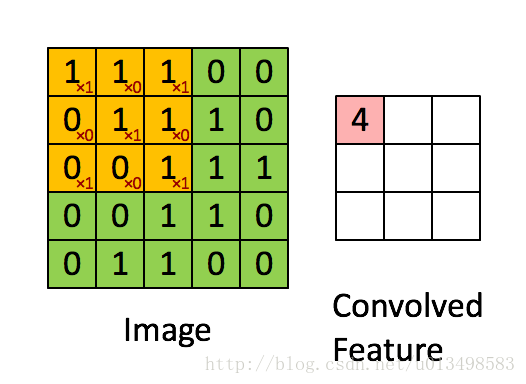
1的计算过程：

第一个通道和对应权重的结果：0*1+0*1+0*(-1)+0*(-1)+0*0+1*1+0*(-1)+0*(-1)+1*0 = 1

第二个通道和对应权重的结果：0*(-1)+0*0+0*(-1)+0*0+1*0+1*(-1)+0*1+0*(-1)+2*0 = -1

第三个通道和对应权重的结果：0*0+0*1+0*0+0*1+2*0+0*1+0*0+0*(-1)+0*0 = 0

偏置：1  所以1+（-1）+ 0 + 1 = 1

转载自https://blog.youkuaiyun.com/cheneykl/article/details/79740810