一下午只弄清楚这一个问题了,记录一下,有点乱:
先从线性回归问题说起,为了对样本点进行拟合求得拟合函数来进行对新的输入做出预测,便设计了一个衡量拟合函数好坏的标准,其实标准有很多:可以是SUM{|f(Xi) - Yi|} / N; 也可以是SUM{|f(Xi) - Yi|^2} / N;
因为对于不同的拟合函数,样本点是相同的,那N就是一样的,所以可以直接比较:
1.SUM{|f(Xi) - Yi|}
或者
2.SUM{|f(Xi) - Yi|^2}
那么再说说为什么都比较喜欢用SUM{|f(Xi) - Yi|^2}呢?为什么都喜欢用平方呢?我看到过两种殊途同归的解释,大概是这样子的:
一、根据最大似然估计来解释:
最大似然估计的思想是寻找一种分布,使得当前样本出现的概率最大!
这个样本出现的概率可以表示成各个样本出现的概率的乘积,当然可以取个对数,变成logP的加和。
接着我们做一个假设:
假设当前样本服从的那个真实的分布函数为F(X),在点Xi处采样得到的样本服从以F(Xi)为均值的正态分布(因为有噪声,否则就应该是准确的F(Xi)而不会有偏差了),我们可以先不考虑珍这个正态分布的方差,但假设各个点采样服从的正态分布的方差是相同的。
先不争论这样的假设是否合理,具体我也不知道合理不合理,只是感觉还算合理!
在这样的假设前提下,样本点<Xi, Yi>出现的概率正比于Exp(-(Yi-F(Xi))^2),这个就是根据正态分布的密度函数而来的,具体不要纠结于准确的形式,主要是看那个差的平方。
用你给出现拟合函数f(x)替代这里的真正的分布函数F(X),依照最大似然估计的思想就是让Exp(-SUM{|f(Xi) - Yi|^2})取得最大值。这样就可以解释为什么要用最小二乘的形式来作为衡量拟合函数的标准的原因了吧!
二、根据贝叶斯理论
给出一个拟合函数,评价好坏的标准是根据样本的后验概率来裁决;这个感觉跟最大似然估计很像啊。关于样本分布做出的假设与前面是一样的,那后验概率的公式是什么呢?是这样的:P(h|D) ∝ P(h) * P(D|h)
这里的h指的是拟合函数,D指的是样本点,那正比式子的右边是拟合函数的先验概率乘以该拟合函数得出该样本点的概率,左边就是对应的后验概率了,就是根据样本点得出目标函数的概率。而各个拟合函数的先验概率是P(h)是相同的,谁也不比谁更好!所以只用看P(D|h)就可以了,而根据前面做出的假设,这个条件概率也是正比于Exp(-(Yi-F(Xi))^2)的。考虑全部的样本点,整体的后验概率是各个样本点的概率的乘积,就又回到了Exp(-SUM{|f(Xi) - Yi|^2})这个式子上去了~~~~
回来说这个最小二乘的问题怎么解呢?如何求得它的最小值呢?可以直接对各个参数求导数,令导数等于0,联立解方程组!
这就是标准最小二乘法的解法,会得到目标函数的一个解析解,关于这个解析解是怎么解出来的,我目前还不知道,只是看到结果里需要对矩阵求逆。标准解法的效率比较低,因为涉及到矩阵运算,计算量太大,所以转而用梯度下降法来解,在介绍梯度下降法之前,先说明,因为最小二乘问题是一个求凸函数极值的问题,它只有一个最优解,没有所谓的局部最优,所以在这个问题上完全可以大胆放心的用梯度下降来解,一开始这里我一直没有想明白,因为网上很多介绍梯度下降的总是说不保证全局最优,他们说的没错,但在这个问题上不会出现。
关于梯度下降法、随机梯度下降法、批量梯度下降法:
这里有篇定义,我觉得定义的很好:http://www.cnblogs.com/549294286/archive/2012/12/13/2817204.html
一、梯度gradient
http://zh.wikipedia.org/wiki/%E6%A2%AF%E5%BA%A6
在标量场f中的一点处存在一个矢量G,该矢量方向为f在该点处变化率最大的方向,其模也等于这个最大变化率的数值,则矢量G称为标量场f的梯度。
标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
更严格的说,从欧氏空间Rn到R的函数的梯度是在Rn某一点最佳的线性近似。在这个意义上,梯度是雅戈比矩阵的一个特殊情况。
在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜率。
梯度一词有时用于斜度,也就是一个曲面沿着给定方向的倾斜程度。
一个标量函数 的梯度记为:
的梯度记为: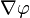 或
或  , 其中
, 其中 (nabla)表示矢量微分算子。
(nabla)表示矢量微分算子。
二、梯度下降法
http://zh.wikipedia.org/wiki/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B3%95
梯度下降法,基于这样的观察:
如果实值函数  在点
在点  处可微且有定义,那么函数
处可微且有定义,那么函数  在
在  点沿着梯度相反的方向
点沿着梯度相反的方向  下降最快。因而,如果
下降最快。因而,如果
对于  为一个够小数值时成立,那么
为一个够小数值时成立,那么 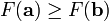 。
。
 是向量。
是向量。
考虑到这一点,我们可以从函数  的局部极小值的初始估计
的局部极小值的初始估计  出发,并考虑如下序列
出发,并考虑如下序列 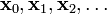 使得
使得
因此可得到
如果顺利的话序列 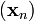 收敛到期望的极值。注意每次迭代步长
收敛到期望的极值。注意每次迭代步长  可以改变。
可以改变。
梯度下降法的缺点是:
- 靠近极小值时速度减慢。
- 直线搜索可能会产生一些问题。
- 可能会'之字型'地下降。
三、随机梯度下降法stochastic gradient descent,也叫增量梯度下降
由于梯度下降法收敛速度慢,而随机梯度下降法会快很多
–根据某个单独样例的误差增量计算权值更新,得到近似的梯度下降搜索(随机取一个样例)
–可以看作为每个单独的训练样例定义不同的误差函数
–在迭代所有训练样例时,这些权值更新的序列给出了对于原来误差函数的梯度下降的一个合理近似
–通过使下降速率的值足够小,可以使随机梯度下降以任意程度接近于真实梯度下降
•标准梯度下降和随机梯度下降之间的关键区别
–标准梯度下降是在权值更新前对所有样例汇总误差,而随机梯度下降的权值是通过考查某个训练样例来更新的
–在标准梯度下降中,权值更新的每一步对多个样例求和,需要更多的计算
–标准梯度下降,由于使用真正的梯度,标准梯度下降对于每一次权值更新经常使用比随机梯度下降大的步长
–如果标准误差曲面有多个局部极小值,随机梯度下降有时可能避免陷入这些局部极小值中(此处没有这种情况出现)
再贴一篇写的很好的:http://blog.youkuaiyun.com/zhang_2348/article/details/8580062
梯度下降算法是利用梯度下降的方向迭代寻找目标函数的参数的最优值。

它遵循LMS(Least Mean Square是)准则,该准则是通过使似然函数最大推导得出,即得出的参数使得样本数据集出现的概率最大。
常用的迭代方法有两种:批量梯度下降法(Batch Gradient Descent)和随机梯度下降法(Stochastic Gradient Descent)。
批量梯度下降是一种对参数的update进行累积,然后批量更新的一种方式。用于在已知整个训练集时的一种训练方式,但对于大规模数据并不合适。
随机梯度下降是一种对参数随着样本训练,一个一个的及时update的方式。常用于大规模训练集,当往往容易收敛到局部最优解。
批量梯度下降法(Batch Gradient Descent):

随机梯度下降法(Stochastic Gradient Descent):

梯度下降算法对局部极值敏感,但是对于线性回归问题只有整体极值,没有局部极值,所以在这种情况下,算法总是收敛的。
对于随机梯度下降算法,其收敛速度要快于批量梯度下降算法,但是它在最小值附近震荡的幅度较大,所以可能不会收敛于true minimum。
再补充一个关于批处理梯度下降、随机梯度下降、mini梯度下降、average梯度下降的简介
http://blog.sina.com.cn/s/blog_eb3aea990101e6p8.html
写的挺好的!





 本文详细介绍了线性回归问题中衡量拟合函数好坏的标准,为何偏好平方误差,以及最小二乘法背后的数学原理。进一步阐述了梯度下降法、随机梯度下降法和批量梯度下降法的概念、优点和应用场景。
本文详细介绍了线性回归问题中衡量拟合函数好坏的标准,为何偏好平方误差,以及最小二乘法背后的数学原理。进一步阐述了梯度下降法、随机梯度下降法和批量梯度下降法的概念、优点和应用场景。
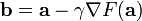
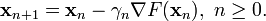
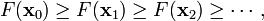
















 13万+
13万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








