可验证延迟函数（VDF）

最新推荐文章于 2025-08-26 11:15:48 发布

原创最新推荐文章于 2025-08-26 11:15:48 发布 · 5.7k 阅读

10 ·

CC 4.0 BY-SA版权

基础理论专栏收录该内容

152 篇文章

订阅专栏

可验证延迟函数（Verifiable Delay Function, VDF）：
VDF 这个概念最初由斯坦福大学密码学教授 Dan Boneh 等人在2018年论文《Verifiable Delay Functions》中给出。该篇文章于 2018 年发表在密码学顶级会议之一的 CRYPTO 上。

目前的VDF算法复杂度较高，离实用仍有差距。

https://github.com/Chia-Network/vdf-competition/中有对VDF的实现进行了竞赛。

[研究]可验证延迟函数（VDF）（一）一文搞懂VDF中有很详细的介绍。

https://github.com/cambrian/accumulator/blob/master/src/group/class.rs中有对https://github.com/Chia-Network/vdf-competition/blob/master/classgroups.pdf的class group 做实现。

VDF是串行运算算法，执行时间可预知，且无法通过并行来加速。通过VDF生成的证明可被快速verify。
目前知名的不可并行的串行运算为：对未知order的group进行repeated squaring。
The unknown order requirement is due to the divisibility of the order of a finite group by the order of any element in the group; if the group order is known then the repeated squaring operation could be reduced modulo the order of the group, shortcutting the computation.

在VDF中：

若使用RSA group，则需要trusted setup，并保证生成后的有毒垃圾被即时清理，否则VDF的sequentiality requirement将broken。
若使用class group of binary quadratic form将不需要trusted setup。因为其order为一个负素数判别式 $d$ ，当 $|d|\equiv 3\ mod\ 4$ 时，is believed to be difficult to compute when $d$ is sufficiently large, making the order of the class group effectively unknown. Therefore, a suitable discriminant ——and its associated class group —— can be chosen without the need for a trusted setup, which is a major advantage for using class groups in applications requiring groups of unknown order.

1. Binary quadratic form

$f(x,y)=ax^2+bxy+cy^2$ , where $a,b,c\in R$ and $a! = 0, b! = 0, c! = 0$ 。
$f = (a, b, c)$ 可称为a form。
若 $f = (a, b, c)$ , where $a,b,c\in Z$ and $a! = 0, b! = 0, c! = 0$ ，则 f 称为integral form。
$c o n f (f) = g c d (a, b, c)$ 称为content of a form。
若 $c o n f (f) = 1$ ，则form f称为primitive。
discriminant of form f为： $\Delta(f)=b^2-4ac$ 。
若 $-a<b\leq a$ ，则form $f = (a, b, c)$ 称为normal。

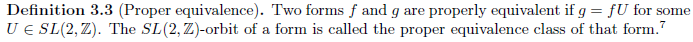
在这里插入图片描述

1.1 Normalization操作

Normalization操作（当 $-a<b\leq a$ 时，需要进行此操作， Normalization操作不会影响discriminant值，即 $b^2-4ac$ 保持不变。）：
$\eta(f)=\eta(a,b,c)=(a,b+2ra,ar^2+br+c)$ ，其中 $r=\left \lfloor \frac{a-b}{2a} \right \rfloor$ 。
若 $f_{norm}=(a',b',c')=\eta(a,b,c)$ ， $f = (a, b, c)$ ，则 $f_{norm}\sim f$ 两者等价：
$U=\begin{pmatrix} 1&r \\ 0&1 \end{pmatrix}$ ， $fU)(x,y)=f_{norm}$ 。
在这里插入图片描述

1.2 Reduced form

在Chia VDF中频繁地reduce $f (a, b, c)$ 非常重要，可保证在做平方运算时，a,b,c的值不会增长过大。
若 $f = (a, b, c)$ 已为normal，且 $a < c$ 或者当 $a=c时，b\geq0$ ，则称 f 为Reduced form。
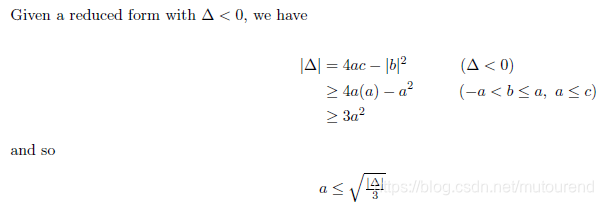
在这里插入图片描述

1.3 Reduction操作

在reduction操作之前应先进行normalization操作。
Reduction操作为（当 $a > c$ 时或 $a=c\ and\ b<0$ ，需要进行此操作， Reduction操作不会影响discriminant值，即 $b^2-4ac$ 保持不变。）：
对于 $f = (a, b, c)$ ，有reduction操作 $\rho(f)=\rho(a,b,c)=(c,-b+2sc,cs^2-bs+a)$ ，其中 $r=\left \lfloor \frac{c+b}{2c} \right \rfloor$

$\rho(a,b,c)\sim \eta(c,-b,a)$ 两者等价。
若 $f_{red}=(a',b',c')=\rho(a,b,c)$ ，则 $f=(a,b,c)\sim f_{red}$ 两者等价，其中的 $U=\begin{pmatrix} 0&-1 \\ 1&r \end{pmatrix}$ ， $fU)(x,y)=f_{red}$ 。
在这里插入图片描述
如上图所示，reduction算法会循环执行步骤2，以保证最终获得reduced form。执行步骤2的次数为：

在这里插入图片描述

1.4 composition计算

在这里插入图片描述

1.4.1 squaring算法

在这里插入图片描述

1.4.2 linear congruence算法

在这里插入图片描述

2. Matrix表示a form

$M(f)=\begin{pmatrix} a&b/2 \\ b/2&c \end{pmatrix}$ ，其中 $det(M(f))=ac-\frac{b^2}{4}$
若 $X=\begin{pmatrix} x&y \end{pmatrix}$ ，则有：
$f(x,y)=ax^2+bxy+cy^2=X\ M(f)\ X^T =\begin{pmatrix} x&y \end{pmatrix}\begin{pmatrix} a&b/2 \\ b/2&c \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$