dalek-Curve25519 avx2并行计算学习笔记

最新推荐文章于 2025-09-16 08:57:31 发布

原创最新推荐文章于 2025-09-16 08:57:31 发布 · 809 阅读

CC 4.0 BY-SA版权

本文深入解析了Curve25519在有限域2^255-19内的并行计算方法，包括使用AVX2指令集进行的FieldElement表示和运算，以及基于Extend twisted坐标系的double和add算法。通过分析，揭示了如何将串行算法转化为高效的并行计算方案。

1. 引言

Curve25519 Field Element在有限域 $2^{255}-19$ 域内，采用64bit 串行计算时，采用的是5个FieldElement51元素来表示一个Element；若采用32-bit AVX2并行计算，则每个Element由10个FieldElement2526元素来表示。
即对于某Curve25519 Field Element a，对应的32-bit AVX2表示为（其中 $若\ i\%2==0,\ a_i<2^{26}<2^{32}; else\ a_i<2^{25}<2^{32}$ ）：

$a_9$	$a_8$	$a_7$	$a_6$	$a_5$	$a_4$	$a_3$	$a_2$	$a_1$	$a_0$

/// Given an array of wide coefficients, reduce them to a `FieldElement2625x4`.
    ///
    /// # Postconditions
    ///
    /// The coefficients of the result are bounded with \\( b < 0.007 \\).
    #[inline]
    fn reduce64(mut z: [u64x4; 10]) -> FieldElement2625x4 {
        // These aren't const because splat isn't a const fn
        let LOW_25_BITS: u64x4 = u64x4::splat((1 << 25) - 1);
        let LOW_26_BITS: u64x4 = u64x4::splat((1 << 26) - 1);

        // Carry the value from limb i = 0..8 to limb i+1
        let carry = |z: &mut [u64x4; 10], i: usize| {
            debug_assert!(i < 9);
            if i % 2 == 0 {
                // Even limbs have 26 bits
                z[i + 1] = z[i + 1] + (z[i] >> 26);
                z[i] = z[i] & LOW_26_BITS;
            } else {
                // Odd limbs have 25 bits
                z[i + 1] = z[i + 1] + (z[i] >> 25);
                z[i] = z[i] & LOW_25_BITS;
            }
        };

        // Perform two halves of the carry chain in parallel.
        carry(&mut z, 0); carry(&mut z, 4);
        carry(&mut z, 1); carry(&mut z, 5);
        carry(&mut z, 2); carry(&mut z, 6);
        carry(&mut z, 3); carry(&mut z, 7);
        // Since z[3] < 2^64, c < 2^(64-25) = 2^39,
        // so    z[4] < 2^26 + 2^39 < 2^39.0002
        carry(&mut z, 4); carry(&mut z, 8);
        // Now z[4] < 2^26
        // and z[5] < 2^25 + 2^13.0002 < 2^25.0004 (good enough)

        // Last carry has a multiplication by 19.  In the serial case we
        // do a 64-bit multiplication by 19, but here we want to do a
        // 32-bit multiplication.  However, if we only know z[9] < 2^64,
        // the carry is bounded as c < 2^(64-25) = 2^39, which is too
        // big.  To ensure c < 2^32, we would need z[9] < 2^57.
        // Instead, we split the carry in two, with c = c_0 + c_1*2^26.

        let c = z[9] >> 25;
        z[9] = z[9] & LOW_25_BITS;
        let mut c0: u64x4 = c & LOW_26_BITS; // c0 < 2^26;
        let mut c1: u64x4 = c >> 26;         // c1 < 2^(39-26) = 2^13;

        unsafe {
            use core::arch::x86_64::_mm256_mul_epu32;
            let x19 = u64x4::splat(19);
            c0 = _mm256_mul_epu32(c0.into_bits(), x19.into_bits()).into_bits(); // c0 < 2^30.25
            c1 = _mm256_mul_epu32(c1.into_bits(), x19.into_bits()).into_bits(); // c1 < 2^17.25
        }

        z[0] = z[0] + c0; // z0 < 2^26 + 2^30.25 < 2^30.33
        z[1] = z[1] + c1; // z1 < 2^25 + 2^17.25 < 2^25.0067
        carry(&mut z, 0); // z0 < 2^26, z1 < 2^25.0067 + 2^4.33 = 2^25.007

        // The output coefficients are bounded with
        //
        // b = 0.007  for z[1]
        // b = 0.0004 for z[5]
        // b = 0      for other z[i].
        //
        // So the packed result is bounded with b = 0.007.
        FieldElement2625x4([
            repack_pair(z[0].into_bits(), z[1].into_bits()),
            repack_pair(z[2].into_bits(), z[3].into_bits()),
            repack_pair(z[4].into_bits(), z[5].into_bits()),
            repack_pair(z[6].into_bits(), z[7].into_bits()),
            repack_pair(z[8].into_bits(), z[9].into_bits()),
        ])
    }

2. vector (a,b,c,d)表示

根据博客CPU指令集——AVX2第四节内容有：
在这里插入图片描述

所以有：

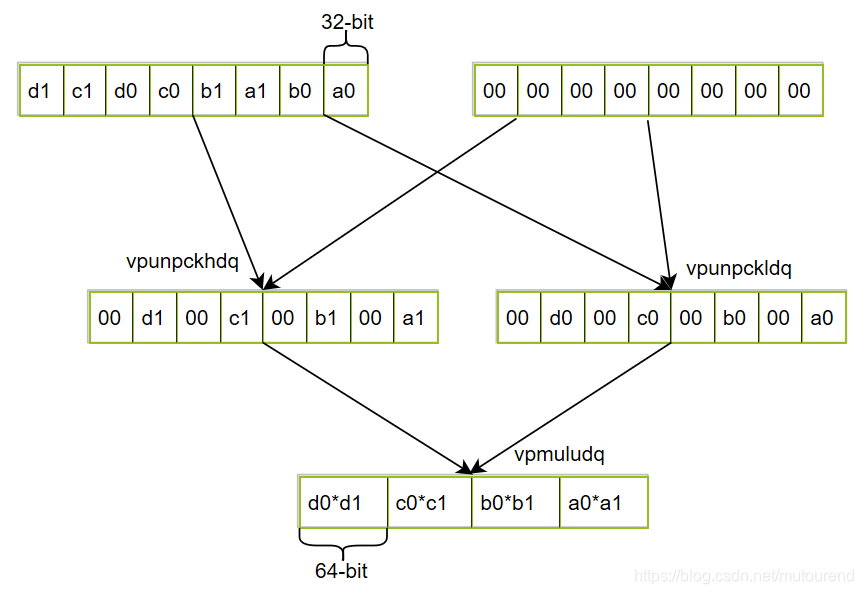
对于4 field elements vector $(a, b, c, d)$ 可以 $[u32\times8;5]$ 数组（以little-endian形式）来表示：
$a_0,b_0,a_1,b_1,c_0,d_0,c_1,d_1)$
$a_2,b_2,a_3,b_3,c_2,d_2,c_3,d_3)$
$a_4,b_4,a_5,b_5,c_4,d_4,c_5,d_5)$
$a_6,b_6,a_7,b_7,c_6,d_6,c_7,d_7)$
$a_8,b_8,a_9,b_9,c_8,d_8,c_9,d_9)$

亦即对于4 field elements vector $(a, b, c, d)$ ，可以FieldElement2625x4表示为：

/// A vector of four field elements.
///
/// Each operation on a `FieldElement2625x4` has documented effects on
/// the bounds of the coefficients.  This API is designed for speed
/// and not safety; it is the caller's responsibility to ensure that
/// the post-conditions of one operation are compatible with the
/// pre-conditions of the next.
#[derive(Clone, Copy, Debug)]
pub struct FieldElement2625x4(pub(crate) [u32x8; 5]);

根据FieldElement2625x4与vector $(a, b, c, d)$ 之间的相互转换需借助unpack_pair函数和repack_pair函数：

/// Unpack 32-bit lanes into 64-bit lanes:
/// ```ascii,no_run
/// (a0, b0, a1, b1, c0, d0, c1, d1)
/// ```
/// into
/// ```ascii,no_run
/// (a0, 0, b0, 0, c0, 0, d0, 0)
/// (a1, 0, b1, 0, c1, 0, d1, 0)
/// ```
#[inline(always)]
fn unpack_pair(src: u32x8) -> (u32x8, u32x8) {
    let a: u32x8;
    let b: u32x8;
    let zero = i32x8::new(0, 0, 0, 0, 0, 0, 0, 0);
    unsafe {
        use core::arch::x86_64::_mm256_unpackhi_epi32;
        use core::arch::x86_64::_mm256_unpacklo_epi32;
        a = _mm256_unpacklo_epi32(src.into_bits(), zero.into_bits()).into_bits();
        b = _mm256_unpackhi_epi32(src.into_bits(), zero.into_bits()).into_bits();
    }
    (a, b)
}
/// Repack 64-bit lanes into 32-bit lanes:
/// ```ascii,no_run
/// (a0, 0, b0, 0, c0, 0, d0, 0)
/// (a1, 0, b1, 0, c1, 0, d1, 0)
/// ```
/// into
/// ```ascii,no_run
/// (a0, b0, a1, b1, c0, d0, c1, d1)
/// ```
#[inline(always)]
fn repack_pair(x: u32x8, y: u32x8) -> u32x8 {
    unsafe {
        use core::arch::x86_64::_mm256_blend_epi32;
        use core::arch::x86_64::_mm256_shuffle_epi32;

        // Input: x = (a0, 0, b0, 0, c0, 0, d0, 0)
        // Input: y = (a1, 0, b1, 0, c1, 0, d1, 0)

        let x_shuffled = _mm256_shuffle_epi32(x.into_bits(), 0b11_01_10_00);
        let y_shuffled = _mm256_shuffle_epi32(y.into_bits(), 0b10_00_11_01);

        // x' = (a0, b0,  0,  0, c0, d0,  0,  0)
        // y' = ( 0,  0, a1, b1,  0,  0, c1, d1)

        return _mm256_blend_epi32(x_shuffled, y_shuffled, 0b11001100).into_bits();
    }
}

3. 对于Extend twisted坐标系表示的点 $X_1,Y_1,Z_1,T_1)$ 的double/add运算

根据论文《Twisted Edwards Curves Revisited》中有相应的串行和并行运算算法：
在这里插入图片描述

3.1 对于Extend twisted坐标系表示的点 $X_1,Y_1,Z_1,T_1)$ 的double运算

double算法与实际代码实现中的映射关系为：
$R_6=R_2+R_3=S_1+S_2=S_5$
$R_7=R_2-R_3=S_1-S_2=S_6$
$R_1=R_4+R_7=2S_3+S_1-S_2=S_8$
$R_2=R_6-R_5=S_1+S_2-S_4=S_9$
对应地有：
$S_9,0,S_6,0,S_6,0,S_9,0)\ vpmuludq\ (S_8,0,S_5,0,S_8,0,S_5,0)=(S_8*S_9,S_6*S_5,S_6*S_8,S_9*S_5)=(X_3,Y_3,Z_3,T_3)$

根据博客curve25519-dalek中field reduce原理分析可知，radix为25.5时有： $\because 2^{255}*x^{10} \equiv 19 \quad mod \quad (2^{255}-19)， when\ x=1.$
以及博客Curve25519 Field域2^255-19内的快速运算，以radix-25.5为例，符合avx2并行计算的设计。对于一个FieldElement，可表示为：
$f=f_0+f_12^{26}x+f_22^{51}x^2+f_32^{77}x^3+f_42^{102}x^4+f_52^{128}x^5+f_62^{153}x^6+f_72^{179}x^7+f_82^{204}x^8+f_92^{230}x^9$
$g=g_0+g_12^{26}x+g_22^{51}x^2+g_32^{77}x^3+g_42^{102}x^4+g_52^{128}x^5+g_62^{153}x^6+g_72^{179}x^7+g_82^{204}x^8+g_92^{230}x^9$
根据论文《Sandy2x: New Curve25519 Speed Records》有：
在这里插入图片描述

3.2 对于Extend twisted坐标系表示的点 $X_1,Y_1,Z_1,T_1),(X_2,Y_2,Z_2,T_2)$ 的add运算

论文《Twisted Edwards Curves Revisited》并行运算算法设计运行在不同的处理器上，实际软件实现并不可行，因为不同处理器之间的同步效率导致的延时不可接受。（The reason may be that HWCD08 describe their formulas as operating on four independent processors, which would make a software implementation impractical: all of the operations are too low-latency to effectively synchronize.）
在这里插入图片描述
https://doc-internal.dalek.rs/curve25519_dalek/backend/vector/index.html中对以上算法进行了进一步梳理：

其中的M和S分别表示乘法和平方运算，D表示与曲线系数的乘法运算，如上图的 $k = 2 d$ 。对于Curve25519的曲线表示为： $x^2+y^2=1+dx^2y^2, d=-(121665/121666),q=2^{255}-19$ 。
其中的M和S具有很好的一致性，适于扩展至vector并行计算。
$k = 2 d$ 也可转换为以4个元素的vector表示： $k=2d=k_0+2^nk_1+2^{2n}k_2+2^{3n}k_3$ ，这样就可以直接并行计算 $k_i*R_7$ 。
当 $d=\frac{d_1}{d_2}=\frac{-121665}{121666}$ 时，以下坐标表示等价：
$(R_5,R_6,2\frac{d_1}{d_2}R_7,2R_8)\leftarrow(d_2R_5,d_2R_6,2d_1R_7,2d_2R_8)$