数据结构
1.链表
(1)单链表
c语言实现:
typedef struct Lnode {
Elemtype e;
struct Lnode *next
}Lnode, *Linklist;
JAVA语言实现:
public class Node{
public Object data;
public Node next;
public Node(Object e){
this.data = e;
}
}
2.栈
typedef struct {
SElemtype *top;
SElemtype *base;
int stacksize;
}SqStack;
JAVA语言实现:
//节点
public class LinkNode<T> {
private T data;
private LinkNode<T> next;
public LinkNode(T data, LinkNode<T> next){
this.data = data;
this.next = next;
}
}
//实现栈
public class LinkStack<T>{
private LinkNode base;
private LinkNode top;
private Integer size;
public void InitStack(){
top = base = new LinkNode();
size = 0;
}
}
3.队列
C语言实现:
typedef struct {
QElemtype *base;
int front;
int rear;
}SqQueue;
JAVA语言实现:
//节点
public class LinkNode<T> {
private T data;
private LinkNode<T> next;
public LinkNode(T data, LinkNode<T> next){
this.data = data;
this.next = next;
}
}
//实现队列
public class LinkQueue<T>{
private LinkNode rear;
private LinkNode front;
private Integer size;
public void InitStack(){
front = rear = new LinkNode();
size = 0;
}
}
4.二叉树
(1)满二叉树和完全二叉树
满二叉树:深度为k,且有2^k-1个节点。
完全二叉树:深度为k,不需有2^k-1个节点,但是每个节点需按照层次遍历排列。
(2)遍历二叉树
先序遍历
中序遍历
后序遍历
三种遍历都有使用二叉链表进行递归和非递归实现方法。
C语言二叉树:
typedef struct BiTNode{
TElemtype data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
递归实现先序遍历:
Status PreOrderTraverse(BiTree T, Status(*Visit)(TElemType e)){
//Visit函数:
//Status PrintElement(TElemType e){
// printf(e);
// return OK;
//}
if(T){
if(Visit(T->data))
if(PreOrderTraverse(T->lchild,Visit))
if(PreOrderTraverse(T->rchild,Visit)) return OK;
return ERROR;
}else return OK;
}
非递归实现中序遍历:
Status InOrderTraverse(BiTree T, Status(*Visit)(TElemType e)){
InitStack(S);
p = T;
while(p||!StackEmpty(S)){
if(p){
Push(S,p);
p = p->lchild;
}
else{
Pop(S,p);
P=P->rchild;
}
}
return OK;
}
JAVA实现二叉树:
//节点
public class BiNode{
public BiNode left;
public BiNode right;
private Object data;
public BiNode(Object data){
this.data = data;
}
//二叉树的建立
public List<BiNode> createTree(){
int[] array = {1,2,3,4,5,6,7,8,9};
List<BiNode> nodeList = new ArrayList<>();
for(int Index = 0; Index < array.length; Index++){
nodeList.add(new BiNode(array[nodeIndex]));
}
for(Index = 0; Index < array.length/2-1;Index++){
nodeList.get(Index).left = nodeList.get(Index*2 + 1);
nodeList.get(Index).right = nodeList.get(Index*2 + 2);
}
//最后一个父节点,可能存在没有右孩子的情况,所以拿出来单独处理
int lastParentIndex = array.length/2-1;
//左孩子
nodeList.get(lastParentIndex).left = nodeList.get(lastParentIndex * 2 + 1);
//右孩子,如果长度为奇数则建立右孩子
if(array.length % 2 == 1){
nodeList.get(lastParentIndex).right = nodeList.get(lastParentIndex * 2 + 2);
}
return nodeList;
}
JAVA二叉树前序遍历(递归):
public static void PreOrderTraverse(BiNode node){
if(node == null)
return;
System.out.print(node.key + " ");
PreOrderTraverse(node.left);
PreOrderTraverse(node.right);
}
JAVA二叉树中序遍历(非递归):
public void InOrderTraverse(BiNode node){
Stack<BiNode> s = new Stack<BiNode>();
BiNode a = node;
while(a != null || !s.empty()){
while(a != null){
s.push(a);
a = a.left;
}
BiNode a = s.pop();
System.out.print(a.data + " ");
if(a.right != null){
a = a.right;
}
else
a = null;
}
}
(3)赫夫曼树
又称最优二叉树,一类带权路径长度最短的树。
如何构造赫夫曼树:
首先,选取权值最小的两个节点作为左右子树构造一棵新的二叉树。置新的二叉树的根节点的权值,为左右节点权值之和。
将新二叉树放回集合,重复进行选取,直到整个赫夫曼树形成。
(4)深度优先遍历(DFS)和广度优先遍历(BFS)
可参考http://www.blogjava.net/fancydeepin/archive/2013/02/03/CPP_BinaryTreeSearch.html
深度优先遍历:可等价于先序遍历。
运用栈的先进后出原理。
广度优先遍历:
运用队列的先进先出原理。
C++实现广度优先遍历:
void breadthFirstSearch(Tree root){
queue<Node *> nodeQueue;
nodeQueue.push(root);
Node *node;
while(!nodeQueue.empty()){
node = nodeQueue.front;
nodeQueue.pop();
printf(format,node->data);
if(node->lchild){
nodeQueue.push(node->lchild);
}
if(node->rchild){
nodeQueue.push(node->rchild);
}
}
}
JAVA实现广度优先遍历:
public static void LevelTraverse(BiNode root){
Queue<BiNode> queue = new LinkedList<>();
queue.add(root);
while(queue.size()>0){
BiNode a = queue.get(0);
queue.remove();
Syetem.out.print(a.data + " ");
if(a.left != null)
queue.add(a.left);
if(a.right != null)
queue.add(a.right);
}
}
5.查找
(1)静态查找表
有序表,折半查找(logn)
(2)动态查找表
二叉排序树(最好logn,最坏n/2)
为使二叉排序树维持在logn,需使用平衡二叉树,即左子树和右子树深度之差不超过1。
B-树和B+树
(3)哈希表
哈希表如何建立
直接定址法:均匀的哈希函数。
数字分析法:取关键字的若干位
平方取中法:平方后的中间几位
折叠法:分隔为相同位数的几部分,再求叠加和
除留余数法:求mod n 的余数
随机数法:关键字长度不等长时用此方法
如何解决冲突:
开放定址法:存入后面的地址中
再哈希法:再计算一个不同的哈希函数
链地址法:地址为i的记录都存在Hash[i]链表中
6.排序
(1)插入排序
直接插入排序:看i位在已经排好的序列里在哪个位置。
时间复杂度:O(n^2)
折半插入排序:折半查找插入位置,仅减少关键字比较次数
时间复杂度:O(n^2)
(2)快速排序
冒泡排序
时间复杂度:O(n^2)
快速排序:第一个数值为轴,所有比他小的放左边,所有比他大的放右边,设两个指针low和high,low在头,high在末尾。首先把轴取出(第一位空了),high开始往前查找,第一个比轴小的,放入轴所在的位置(此时high位置空了)。然后low往后查找,第一个比轴大的,放入high的位置(low的位置又空了)。直至i和j相同,将轴放入这个位置。递归将轴两边也进行快排。
时间复杂度:O(nlogn) ,最坏情况O(n^2)
快排在所有相同时间复杂度算法中平均性能最好。
(3)选择排序
简单选择排序:每趟选最小的放入i位
时间复杂度:O(n^2)
堆排序:构建堆,使得堆顶是最小,所有非终端节点的值都不大于左右孩子节点的值,每次堆顶和堆底对换,拿掉堆底的最小值,然后重新构建堆。
先把无序序列看成完全二叉树,最后一个非终端节点是[n/2]个元素。从[n/2]往前倒,每次使得根节点最小。
时间复杂度:O(nlogn)
最坏的情况也是O(nlogn) ,这是相对快排来说最大优点。
7.平衡二叉树
性质:左右子树都平衡,平衡意味着左右深度差的绝对值不超过1。(我没孩子你可以有,但你的孩子不可能有孩子)
8.B树,B+树
转载自:https://www.cnblogs.com/xueqiuqiu/articles/8779029.html
B树和B+树应用在数据库索引,可以认为是m叉的多路平衡查找树。理论上二叉树查找速度和比较次数都是最小的,不用二叉树的原因是,当数据量大时,整个索引不会全加载到内存,而是会逐一加载每一个硬盘页。这样会涉及到磁盘IO的时间,磁盘IO相对于内存是很慢的。所以我们要用m叉树减少IO次数。
(1)B树,可以认为是m叉的多路平衡查找树,每个节点最多包涵m个孩子,m成为B树的阶。m的大小取决于磁盘页的大小。(有多大房子生多少孩子)
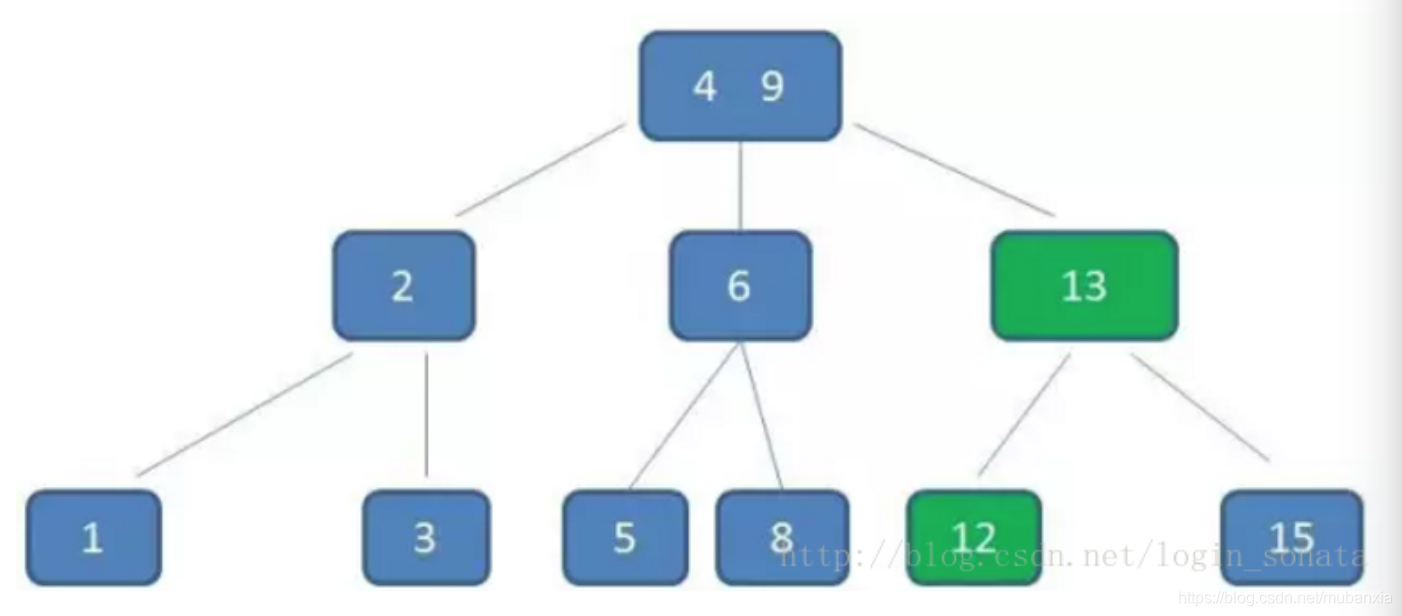
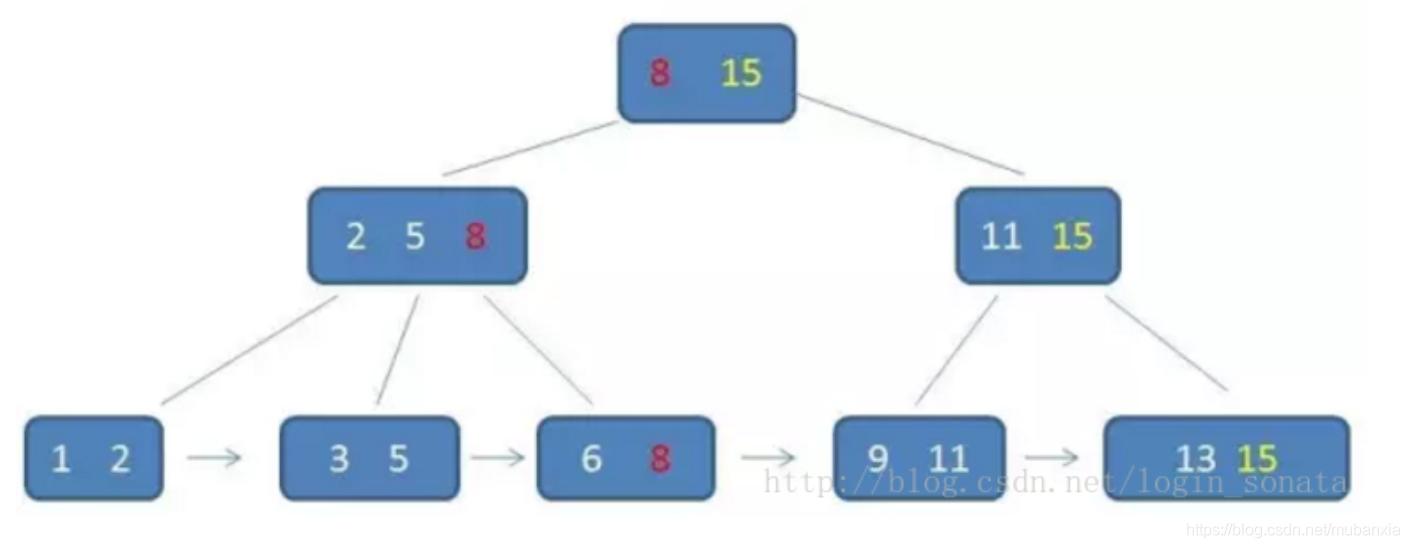
(2)B+树,是B树的变体,查询性能更好。
关键字不再保存数据,只用来索引。所有叶子节点用来保存数据,因此B+树会更矮胖。
同一个节点会在不同节点中重复出现。
因此B+树相对B树的优势就是,B+树只需遍历叶子结点链表,B树需要重复的中序遍历。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








