如何计算句子的相似性-优快云博客

一、基础知识

听起来很高深，其实说起来原理简单，先看个高中的知识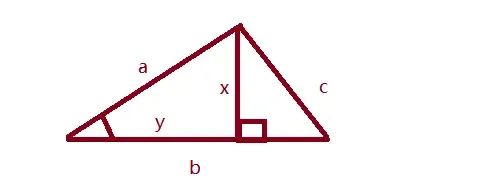：三角形

求图中a和b线夹角的cos值，这个值怎么求那，如果在b的边上做个垂直线x，那么这个角cos计算公式如下：cosA = y/a

计算下：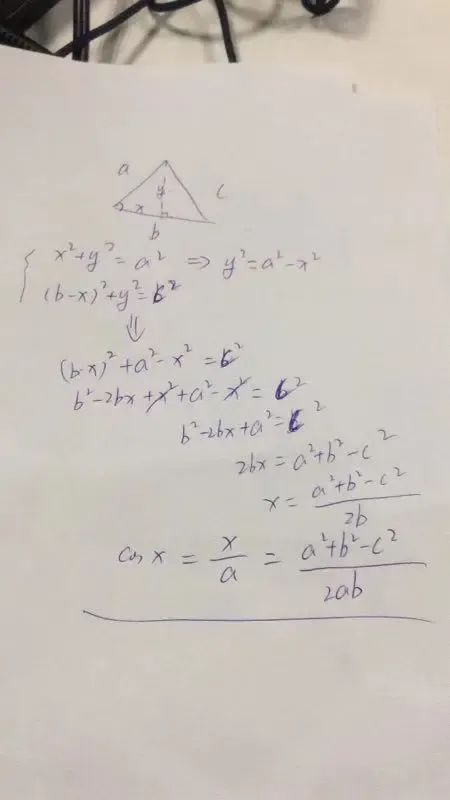

还是同事推导的，我竟然忘记了，汗颜。得出一个余弦计算公式：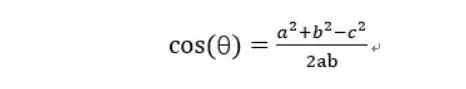

在坐标系中的计算公式如下：在直角坐标系中，向量表示的三角形的余弦函数是怎么样的呢？下图中向量a用坐标(x1,y1)表示，向量b用坐标(x2,y2)表示。

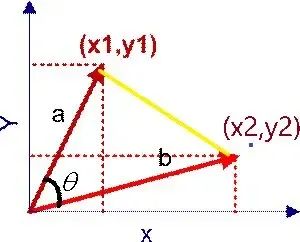坐标系中向量a和向量b在直角坐标中的长度为

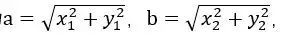
image

，向量a和向量b之间的距离我们用向量c表示，就是上图中的黄色直线，那么向量c在直角坐标系中的长度为

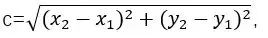
image

，将a，b，c带入三角函数的公式中得到如下的公式：

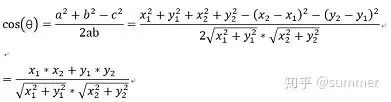这是2维空间中余弦函数的公式，那么多维空间余弦函数的公式就是：

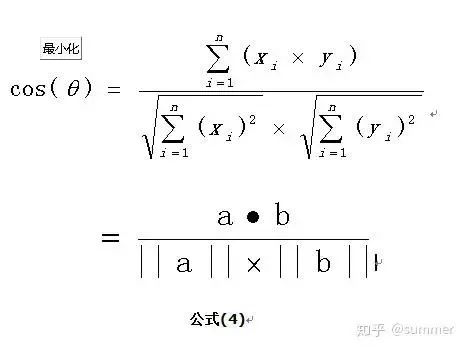
image.png

二、余弦公式有什么用

空间中两个点的距离可以通过余弦来表示，如果余弦值越小，那么角度越大，两个点表示的相似度越低，越接近于1，则越接近。假设有3个物品，item1，item2和item3，用向量表示分别为：

item1[1,1,0,0,1]，

item2[0,0,1,2,1]，

item3[0,0,1,2,0]，

即五维空间中的3个点。用欧式距离公式计算item1、itme2之间的距离，以及item2和item3之间的距离，分别是：

item1-item2=

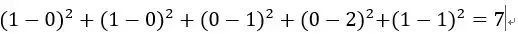
image

item2-item3=

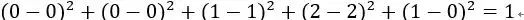
image

用余弦函数计算item1和item2夹角间的余弦值为：

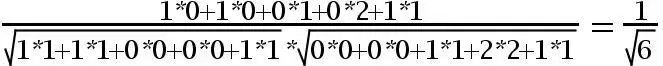
image

用余弦函数计算item2和item3夹角间的余弦值为：

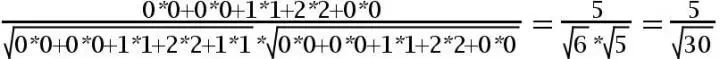
image

由此可得出item1和item2相似度小，两个之间的距离大(距离为7)，item2和itme3相似度大，两者之间的距离小(距离为1)。

余弦相似度算法：一个向量空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小，余弦值接近1，夹角趋于0，表明两个向量越相似，余弦值接近于0，夹角趋于90度，表明两个向量越不相似。

实战代码

我原来看过的别人用one-hot编码，通过计算余弦距离来求两个句子的相关性的代码，但是one-hot编码实质只是对单词出现的频次进行编码，但是每个单词的重要性是不同的，TF-IDF不光计算了单词在文档中的频次，而且对单词是否普通也做了判断。

TF: 即Trem Frequency 即单词在一个文档中出现的次数； IDF: Inverse Document Frequency 即逆向文档频率，标识的是在多少个文档中出现单词的倒数。

TF：标识的是这个单词可以代表的文档的程度；IDF：标识的是这个单词本身的重要性，如果在越多文档中包含这个词，这个词的重要性也就越低。

IDF

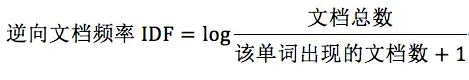
TF-IDF = TF*IDF IDF计算过程中+1防止出现次数为0，用log我像是为了让取值范围更小一些。下面是利用sklearn求的句子的TF-IDF的值，然后计算两个句子之间的相关性，非常简单，代码如下：

# -*- coding: utf-8 -*-
from sklearn.feature_extraction.text import TfidfVectorizer
import math

# 计算余弦距离
def cal_cos(list_one, list_two):
   sum_val = 0
   sq1 = 0
   sq2 = 0
   for i in range(len(list_one)):
       sum_val += list_one[i] * list_two[i]
       sq1 += pow(list_one[i], 2)
       sq2 += pow(list_two[i], 2)
   try:
       result = round(float(sum_val) / (math.sqrt(sq1) * math.sqrt(sq2)), 2)
   except ZeroDivisionError:
       result = 0.0
   return result

if __name__ == '__main__':
   # 初始化 TF-IDF 向量化器，可根据需求设置停用词等参数
   tfidf_vec = TfidfVectorizer(stop_words=['this', 'is', 'and', 'the'])
   # 文本数据
   docs = ['this is the bays document', 'this is the second second document', 'and the third one', 'is this the document']
   # 拟合文本并转换为 TF-IDF 矩阵
   tfidf_matrix = tfidf_vec.fit_transform(docs)
   
   print('不重复的词：', tfidf_vec.get_feature_names_out())
   print('单词的id：', tfidf_vec.vocabulary_)
   print('每个单词的tfidf值：', tfidf_matrix.toarray())
   
   allarray = tfidf_matrix.toarray()
   for i in range(len(docs)):
       r = cal_cos(allarray[0], allarray[i])
       print('第' + str(i) + '个和第0个的相关度为：' + str(r))

计算结果如下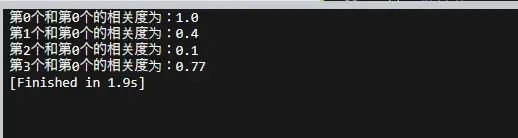：相关度计算我们仔细观察下，和我们的预期类似，这其实就是搜索的基本原理之一了，当然可以去掉停词，注释的代码有相关去掉停词之后再进行计算TF-IDF值的情况。