机器数的表示
1.机器数:
一个数在机器中用最高位表示数的符号,其它位表示数值的大小的这种二进制表示形式,叫做这个数的机器数。 机器数是带符号的,在计算机中,用一个数的最高位存放符号,正数最高位为0,负数最高位为1。
示例:
设计算机字长为8位, 十进制中的数+3,转换成二进制就是0000 0011。 十进制中的数-3,转换成二进制就是1000 0011。 这里的0000 0011和1000 0011就是机器数。
2. 原码:
原码(true form)是一种计算机中对数字的二进制定点表示方法。原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为0,负数该位为1(0有两种表示:+0和-0),其余位表示数值的大小。 设x的原码记作[x]原,如机器字长为n,则原码定义如下 :
 示例: 已知x1=+1010101B, x2=-1011101。 求[x1]原,[x2]原
示例: 已知x1=+1010101B, x2=-1011101。 求[x1]原,[x2]原
则 x1=0 1010101 x2=1 1011101
8位二进制原码表示的范围为: -127~+127
16位二进制原码表示数的范围为:-32767~+32767
“0”的原码有两种表示法:+0=00000000 -0=10000000
1.反码的定义 设数x的反码记作[x]反,如机器字长为n,则反码定义如下:

正数的反码与其原码相同。例如,当机器字长n=8时: [+0]反=[+0]原=00000000B [+35]反=[+35]原=00100011B
负数的反码是在原码基础上,符号位不变(仍为1),数值位按位取反。例如,当机器字长n=8时:[+14]反=00001110 [-14]反=(10101110)反= (28-1)-|X| =(11111111)-(00101110) =11010001
8位二进制反码表示数的范围为: -127~+127
16位二进制反码表示数的范围为: -32767~+32767
[+0]反=00000000B,[-0]反=11111111B
取反的含义 二进制中有0和1两种状态,取反就是取与当前状态相反的状态(相当于电子器件的高低电平)。1取反=0;0取反=1。
3.反码的作用 反码通常用作求补码过程中的中间形式。
补码的概念 一个数x的补码记为[x]补,补码可定义为:

从定义可见,正数的补码=原码,即[x]补=[x]原,所以,只有负数求补的问题。
补码来历:计算机里面,只有加法器,没有减法器,所有的减法运算,都必须用加法进行,用补数代替原数,可把减法转变为加法。
引用补码的目的:是让符号位直接参加运算,以简化加、减运算的规则。
一个数的补码的求法 (1)根据定义求补码 即负数x的补码等于(2n)加上其真值(或减去其真值的绝对值),例如: x=-1010111B,n=8 [x]补=(28)+(-1010111B) =(28)-1010111B =10101001B 这种方法因要做一次减法,很不方便。
2.一个数的补码的求法 (2)利用原码求补码 一个负数的补码等于其原码除符号位保持不变外,其余各位按位取反,再在最低位加1。
例如: x=-1010111B,[x]原=11010111B, [x]补=10101000B+1=10101001B 值得注意的是:0的补码只有唯一的形式,符号位和数值位均为0。无正负0之分。

补码表示的数值范围 用补码表示的数的范围比原码和反码多一个数。
8位二进制原码表示的范围为: -127~+127
8位二进制反码表示数的范围为:-127~+127
8位二进制补码表示数的范围为:-128~+127
移码 移码的符号表示法与原码、反码和补码相反,符号位为1时表示正数,为0时表示负数,其他位与补码相同。因此要求得一个数的移码只需要将其二进制补码的符号位取反即可。
例如
[+9]补=0000 1001 [+9]移=1000 1001 [0 ]补=0000 0000
[0]移=1000 0000 [-127]补=1000 0001 [-127]移=0000 0001
移码是将真值在数轴上往正方向平移了2(n-1)。对8位数,平移了27=128。因此称为移码。移码也称为余码、增码或偏移二进制码。在数/模,模/数转换电路中,经常用到移码。
移码 移码的好处:比较大小比较方便
原码转换为真值 根据原码定义,将原码数值位各位按权展开求和,由符号位决定数的正负即可由原码求出真值。
示例:已知 [x]原=00011111B, [y]原=10011101B, 求x和y。


反码转换为真值
要求反码的真值,只要先求出反码对应的原码,再按上述原码转换为真值得方法即可求出其真值。 正数的原码与反码相同。 负数 的原码可在反码基础上,符号位仍为1不变,数值位按位取反。
示例:已知 [x]反=00001111B, [y]反=11100101B, 求x和y


补码转换为真值 方法:先求出补码对应的原码,再按上述原码转换为真值的方法即可求出其真值。 正数的原码与补码相同。 负数的原码可在补码基础上再次求补,即:
已知 [x]补=00001111B, [y]补=11100101B,求x和y


补码的加减运算
为什么要使用补码运算法
在计算的时候,对于人来说会根据符号位, 选择对真值区域的加减。 如:1-1 = 0
但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单。如果计算机辨别“符号位”显然会让计算机的基础电路设计变得十分复杂,于是人们想出了将符号位也参与运算的方法。根据运算法则减去一个正数等于加上一个负数,如: 1-1 = 1 + (-1) = 0 。所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了。
首先来看原码:计算十进制的表达式: 1-1=0。
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2 。
如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的。这也就是为何计算机内部不使用原码表示一个数。
为了解决原码做减法的问题, 出现了反码: 计算十进制的表达式: 1-1=0 表达式1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题出现在“0”这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的。而且会有[0000 0000]原和[1000 0000]原两个编码表示0。
将符号位参与运算, 并且只保留加法的方法。 为了解决原码做减法的问题, 出现了反码: 计算十进制的表达式: 1-1=0 表达式1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
于是补码的出现, 解决了0的符号以及两个编码的问题: 表达式1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原 。 这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128。
补码加减法的意义:
① 可以将减法运算变为加法运算,因此可使用同一个运算器实现加法和减法运算,简化了电路。
② 无符号数和带符号数的加法运算可以用同一个加法器实现,结果都是正确的。
补码的加法运算 在计算机中,凡是带符号数一律用补码表示,运算结果自然也是补码。
特点:符号位和数值位一起参加运算,并且自动获得结果(包括符号位与数值位)。
规则:[x]补+[y]补=[x+y]补
即:两个数补码的和等于两个数和的补码。不论被加数、加数是正数还是负数,只要直接用它们的补码相加,当结果不超出补码所表示的范围时,计算结果便是正确的补码形式。但当计算结果超出补码表示范围时,结果出错,会出现溢出。
补码减法运算 补码减法的运算规则: [x]补-[y]补=[x]补+[-y]补=[x-y]补
无论被减数、减数是正数还是负数,上述补码减法的规则都是正确的。同样,由最高位向更高位的进位会自动丢失而不影响运算结果的正确性。
优点:
①可以将减法运算变为加法运算,因此可以使用同一个运算器实现加法和减法运算,简化了电路。
② 无符号数和带符号数的加法运算可以用同一个加法器实现,结果都是正确的。
门电路的概念
实现基本和常用逻辑运算的电子电路,叫逻辑门电路。实现“与”运算的叫“与门”,实现“或”运算的叫“或门”,实现“非”运算的叫“非门”,也叫做反相器,等。
分立元件门电路和集成门电路 分立元件门电路:
用分立的元件和导线连接起来构成的门电路。简单、经济、功耗低、负载差。
集成门电路:把构成门电路的元器件和连线都制作在一块半导体芯片上,再封装起来,便构成了集成门电路。常见的是CMOS和TTL集成门电路。
二极管与门
工作原理 A、B为输入信号(+3V或0V),F为输出信号,+Vcc为12V,二极管管压降为0.7V
电路输入与输出电压的关系


逻辑符号

工作波形(又一种表示逻辑功能的方法)
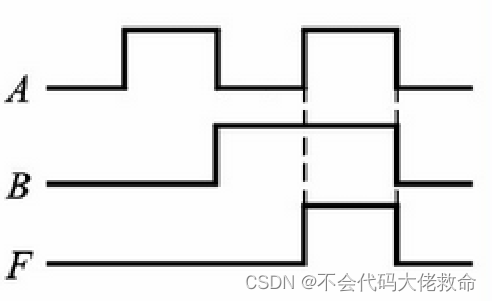
逻辑表达式 F=A∙B 或 F=AΛB
二极管或门
工作波形

逻辑表达式 F=A+B 或 F=AVB
二极管非门(反相器)
逻辑符号

工作波形

逻辑表达式

逻辑门
逻辑门又称“数字逻辑电路基本单元”。执行“或”、“与”、“非”、“或非”、“与非”等逻辑运算的电路。任何复杂的逻辑电路都可由这些逻辑门组成。 常见的逻辑门包括“与”门,“或”门,“非”门,“异或”(也称:互斥或)等等。
逻辑门有两种输出状态 高电平(逻辑1) 低电平(逻辑0)
三态门
三态门(Three-state gate)亦称“三态输出门”、“三态门输出电路”。是一种重要的总线接口电路。具有高电平、低电平和高阻抗三种输出状态的门电路。 一般的逻辑门只有两种输出状态:

三态门有三种输出状态:


三态门比逻辑门增加了一个控制端EN(又称为使能端),当控制端EN有效时,三态门处于工作态,否则处于高阻态。如图所示:



译码器
译码是编码的逆过程,功能是将每个输入的二进制代码,译成对应的输出高、低电平信号。
常用的译码器电路有:二进制译码器 二---十进制译码器 显示译码器
二进制译码器:
二进制 译码器的输入是一组二进制代码,输出是一组与输入代码一 一对应的高、低电平信号。

用二极管与门阵列组成3线—8线译码器
功能:将一组3位二进制代码译成对应的8个输出信号,即有3根输入线(A2,A1,A0),8根输出线(Y0~Y7) 。 组成3线—8线译码器。
设:“1”=H(高电平)=+3V; “0”=L(低电平)=0V;VDON(二极管)压降=0.7V。A2A1A0=000=>Y0=1。如图所示:

3线—8线译码器(74LS138译码器)
74LS138 为3 线-8 线译码器,共有 54/74S138和 54/74LS138 两种线路结构型式。
74LS138的引脚: A0~A2:地址输入端;
/Y0~/Y7:输出端(低电平有效);
VCC:电源正; GND:地;
STA(E1):选通端(高电平有效) ;
/STB(/E2)、/STC(/E3):选通端(低电平有效);
A0~A2对应Y0——Y7;A0,A1,A2以二进制形式输入,然后转换成十进制,对应相应Y的序号输出低电平,其他均为高电平;

3线—8线译码器(74LS138译码器) 74LS138工作原理如下: 当一个选通端(E1)为高电平,另两个选通端(/(E2)和/(E3))为低电平时,可将地址端(A0、A1、A2)的二进制编码在Y0~Y7对应的输出端以低电平译出。(即输出为Y0至Y7的非)比如:A2A1A0=110时,则Y6输出端输出低电平信号。

3线-8线译码器74LS138的功能表: 无论从逻辑图还是功能表都可以看到74LS138的八个输出管脚,任何时刻要么全为高电平1—芯片处于不工作状态,要么只有一个为低电平0,其余7个输出管脚全为高电平1。如果出现两个输出管脚在同一个时间为0的情况,说明该芯片已经损坏。

锁存器 :
锁存器(Latch)是一种对脉冲电平敏感的存储单元电路,它们可以在特定输入脉冲电平作用下改变状态。锁存,就是把信号暂存以维持某种电平状态。
锁存器的最主要作用是缓存,其次完成高速的控制器与慢速的外设的不同步问题,再其次是解决驱动的问题,最后是解决一个 I/O 口既能输出也能输入的问题。
锁存器是利用电平控制数据的输入,它包括不带使能控制的锁存器和带使能控制的锁存器。
三态锁存器
1.三态锁存器74LS373 74LS373是数据锁存器,大大缓解处理器的压力,主要用于解决驱动及扩展问题。
74LS373引脚
D0~D7 数据输入端;
OE 三态允许控制端(低电平有效) LE 锁存允许端;
Q0~Q7 输出端 VCC:电源正;
GND:地;

三态锁存器
1.三态锁存器74LS373 74LS373工作原理:
(1)1脚是输出使能(OE),是低电平有效,当1脚是高电平时,不管输入3、4、7、8、13、14、 17、18 如何,也不管11 脚(锁存控制端,G)如何,输出2(Q0)、5(Q1)、6(Q2)、9(Q3)、12(Q4)、 15(Q5)、16(Q6)、19(Q7)全部呈现高阻状态(或者叫浮空状态);

1.三态锁存器74LS373 74LS373工作原理: (2).当1脚是低电平时,只要11脚(锁存控制端,G)上出现一个下降沿,输出2(Q0)、5(Q1)、 6(Q2)、9(Q3)、12(Q4)、15(Q5)、16(Q6)、19(Q7)立即呈现输入脚3、4、7、8、13、14、17、 18 的状态。
锁存端LE由高变低时,输出端8位信息被锁存,直到LE 端再次有效。 当三态门使能信号OE为低电平时,三态门导通,允许Q0~Q7输出,OE为高电平时,输出悬空。当74LS373用作地址锁存器时,应使OE为低电平,此时锁存使能端C(11脚)为高电平时,输出Q0~Q7 状态与输入端D1~D7状态相同;当C(11脚)发生负的跳变时,输入端D0~D7 数据锁入Q0~Q7。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








