MATLAB中的插值与三维绘图

1.一维插值

MATLAB中的一维插值函数调用格式如下：

y1=interp1（x,y,x1,'method'）

其中，y1为返回x1处的插值结果；x，y为插值结点，即观测数据向量，需要长度一致，同时要求x单调；x1为被插值结点，注意不能超过x的范围；method为所用的插值方法，MATLAB中提供了如下的插值方法对应选项参数：

‘nearest’ 最邻近插值

‘linear’    线性插值

‘spline’   三次样条插值

‘cubic’    立方插值

缺省时   分段线性插值

eg. 从1点到12点的11h内，每隔1h测量一次温度，测得的温度数值依次为5,8,9,15,25,29,31,30,22,25,27,24（单位：℃）。试估计每隔1/10h的温度值。

解：用MATLAB编程如下（三次样条插值）:

clear;clc;
hours=1:12;
temps=[5,8,9,15,25,29,31,30,22,25,27,24];
h=1:.1:12;
t=interp1(hours,temps,h,'spline');
plot(hours,temps,'+',h,t,hours,temps,'r:');
xlabel('时间');ylabel('温度');
legend('观测值','插值后温度变化值');

2.二维插值

z =interp2(x0,y0,x,y,'method')
其中，x0,y0,z0为插值结点，即观测数据向量，要求：

1. x0,y0单调
2. x,y可取为同型矩阵，或一个取行向量，一个取列向量(难理解，可看下面例子)
3. x,y的值分别不超过x0,y0的范围

'method'为所用的插值方法：

‘nearest’ 最邻近插值

‘linear’    双线性插值

‘spline’   三次样条插值

‘cubic’    双三次插值

缺省时   双线性插值

（1）首先，先让我们理解一下meshgrid的用法。简单地说，就是产生Oxy平面的网格坐标。

在进行3-D绘图操作时，涉及到x、y、z三组数据，而x、y这两组数据可以看做是在Oxy平面内对坐标进行采样得到的坐标对（x，y）。例如，要在“3<=x<=5，6<=y<=9，z不限制区间”这个区域内绘制一个3-D图形，如果只需要整数坐标为采样点的话。

我们可能需要下面这样一个坐标构成的矩阵：

(3,9),(4,9),(5,9);

(3,8),(4,8),(5,8);

(3,7),(4,7),(5,7);

(3,6),(4,6),(5,6);

在matlab中我们可以这样描述这个坐标矩阵

把各个点的x坐标独立出来，得：

3,4,5;

3,4,5;

3,4,5;

3,4,5;

再把各个点的y坐标也独立出来：

9,9,9;

8,8,8;

7,7,7;

6,6,6;

这样对应的x、y结合，便表示了上面的坐标矩阵。meshgrid就是产生这样两个矩阵，来简化我们的操作。然后根据(x,y)计算获得z，并绘制出三维图形。

若x=[3,4,5];y=[9;8;7;6]

[x,y]=meshgrid(x,y) 此命令等效于：

x=ones(size(y))*x
y=y’*ones(size(x))

下面，我将通过一个例子来详细说明interp2函数使用要求中的第二小点。

z =interp2(x0,y0,x,y,'method')的使用过程中，x,y要么一个取行向量，一个取列向量（当然，x，y谁是行向量谁是列向量是无所谓的）；也可以为同型矩阵：x，y先取成向量（不要求方向一致），通过meshgrid函数将其转换成同型矩阵，具体用法为:[x,y]=meshgrid(x,y)

(2)eg.

例:测得平板表面3*5网格点处的温度分别如下:

82 81 80 82 84

79 63 61 65 81

84 84 82 85 86

试作出平板表面的温度分布曲面z=f(x,y)的图形。

题目中分布曲面的图形画出来，效果是这样子的：

x=1:5;

y = 1:3;
temps = [82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
mesh(x,y,temps);

从图中可以看出，图形并不是光滑的。我们可以使用二维插值函数进行插值，将其图形变得光滑。那么二维插值函数如何使用呢？我们先使用(以0.2为单位进行作图)，再讲解.

下面给出x,y一个取行向量，一个取列向量的代码（第一种做法）：

x=1:5;
y=1:3;
temps = [82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
xi=1:.2:5;
y1=1:.2:3;
zi=interp2(x,y,temps,xi',y1,'cubic');
mesh(xi,y1,zi); 

 如果x，y为同型矩阵也是可以的：

x=1:5;
y=1:3;
temps = [82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
xi = 1:.2:5;
y1 = 1:.2:3;
[xi,y1]=meshgrid(xi,y1);
zi = interp2(x,y,temps,xi,y1,'cubic');
mesh(xi,y1,zi);

作图仍然和上图一致

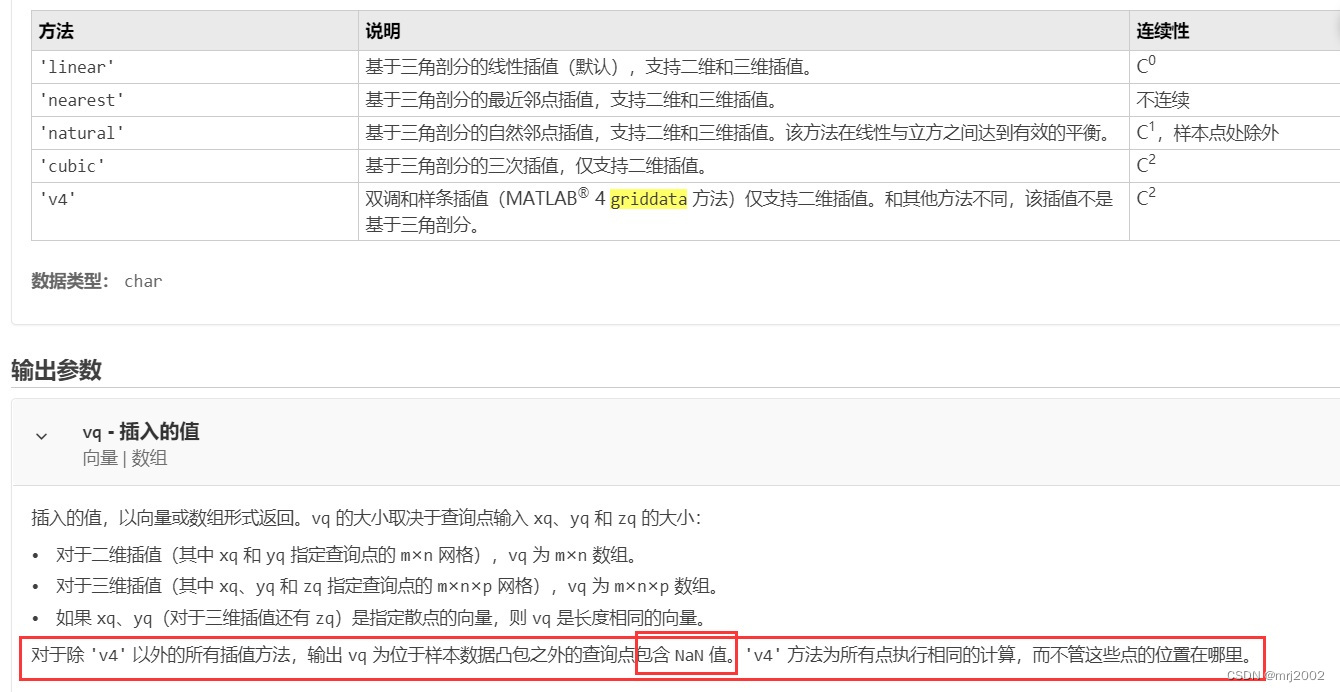
前面介绍的是观测点必须满足单调条件，但实际问题中往往出现观测点是散乱的情况，对此，MATLAB提供了插值函数griddata，其调用格式如下：

4. z1=griddata(x,y,z,x1,y1,'method')

参数说明同二维插值，调用格式与interp2类似，但也有不同，另外，MATLAB提供了一个自带的插值方法，其选项参数为'v4' .在专业性不高的情况下，尽量使用v4插值方法，因为其他方法都是三角网络插值，虽然比较准确，但是可能出现外插的情况，从而出现NaN。

 

下面看一个例子：要求用插值方法绘制地形图。

编号    x(m)    y(m)    海拔(m) 1    74    781    5 2    1373    731    11 3    1321    1791    28 4    0    1787    4 5    1049    2127    12 6    1647    2728    6 7    2883    3617    15 8    2383    3692    7 9    2708    2295    22 10    2933    1767    7 11    4233    895    6 12    4043    1895    14 13    2427    3971    2 14    3526    4357    7 15    5062    4339    5 16    4777    4897    8 17    5868    4904    16 18    6534    5641    6 19    5481    6004    0 20    4592    4603    6 21    2486    5999    2 22&nbs