莫比乌斯反演
https://wenku.baidu.com/view/fbec9c63ba1aa8114431d9ac.html详见此文
测评地址:
1.bzoj 2440 //2440: [中山市选2011]完全平方数 //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2440
2.bzoj 2301 //2301: [HAOI2011]Problem b //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2301
3.bzoj 2820 //P2257 YY的GCD //在线测评地址https://www.luogu.org/problemnew/show/P2257
4.bzoj 3529 //3529: [Sdoi2014]数表 //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3529
5.bzoj 2154 //2154: Crash的数字表格 //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2154
6.bzoj 2693 //bzoj 2693 jzptab
//因该题是bzoj权限题,普通用户无法看到该题,若能将bzoj 2154: Crash的数字表格 尽可能优化,也能达到
//bzoj 2693 jzptab的效果,故采用如下测评地址 2019-7-22 10:48
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2154
题解:
1.bzoj 2440 //2440: [中山市选2011]完全平方数 //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2440
//2440: [中山市选2011]完全平方数
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2440
//题目也有些问题,需说明 1 不算 完全平方数,否则,该题有问题。
//朴素算法,该题极限做到10^7
//试着编一个10^6的朴素算法
输入
3
1
13
100
输出
1
19
163
//以下代码为10^6范围内的朴素代码。2019-7-3 22:29
之前编过该问题,详见https://blog.youkuaiyun.com/mrcrack/article/details/86978764
//试着用容斥原理处理1-20之间的数据
//20/(1*1)=20 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20
//20/(2*2)=5 4=2^2,8=2^2*2,12=2^2*3,16=2^2*4,20=2^2*5
//20/(3*3)=2 9=3^2,18=3^2*2
//20/(5*5)=0
//非平方数的数目为20-5-2=13
//试着用容斥原理处理1-50之间的数据
//50/(1*1)=50 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50
//50/(2*2)=12 4,8,12,16,20,24,28,32,36,40,44,48
//50/(3*3)=5 9,18,27,36,45
//50/(5*5)=2 25,50
//50/(6*6)=1 36
//50/(7*7)=1 49
//非平方数的数目为50-12-5-1+1=33
//sqrt(2*10^9)=44722
//素数筛
//样例最后一个测试点,一直报 段错误
//仔细排查,发现for(i=1;i*i<=x;i++)ans+=x/(i*i)*mu[i];//此处写成for(i=1;i<=x;i++)ans+=x/(i*i)*mu[i];
//修改,样例通过,2019-7-6 11:16
//不取int,取long long,能省去很多烦恼。2019-7-6 11:21
//提交AC.2019-7-6 21:54 以下为AC代码。
#include <stdio.h>
#include <string.h>
#define LL long long
LL not_prime[44722+10],prime[5000],mu[44722+10];
void linear_shaker(LL x){
LL i,j;
memset(not_prime,0,sizeof(not_prime)),memset(prime,0,sizeof(prime)),memset(mu,0,sizeof(mu)),mu[1]=1;
for(i=2;i<=x;i++){
if(!not_prime[i])prime[++prime[0]]=i,mu[i]=-1;
for(j=1;prime[j]*i<=x;j++){
not_prime[prime[j]*i]=1;
if(i%prime[j]==0)break;
mu[prime[j]*i]=-mu[i];
}
}
}
LL judge(LL x){
LL ans=0,i;//ans统计 非完全平方数倍数 个数
for(i=1;i*i<=x;i++)ans+=x/(i*i)*mu[i];//此处写成for(i=1;i<=x;i++)ans+=x/(i*i)*mu[i];//此处写成 for(i=1;i<=x;i++)ans=x/(i*i)*mu[i];
return ans;
}
LL bisection(LL x){
LL left=0,right=x,mid;//技巧,left=0一定能保证 left<k,k<=right,望读者掌握,注意,left=1不取2019-7-6 11:20
while(left+1<right){
mid=(left+right)/2;
if(judge(mid)<x/2)left=mid;
else right=mid;
}
return right;//此处写成return left;
}
int main(){
LL k,t;
linear_shaker(44722);
scanf("%lld",&t);
while(t--){
scanf("%lld",&k);
printf("%lld\n",bisection(2*k));
}
return 0;
}
//2440: [中山市选2011]完全平方数
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2440
//题目也有些问题,需说明 1 不算 完全平方数,否则,该题有问题。
//朴素算法,该题极限做到10^7
//试着编一个10^6的朴素算法
输入
3
1
13
100
输出
1
19
163
//以下代码为10^6范围内的朴素代码。2019-7-3 22:29
#include <stdio.h>
#include <string.h>
#define maxn 1000100
int a[maxn],vis[maxn];
int main(){
int i,j,t,k;
memset(vis,0,sizeof(vis));
for(i=2;i<=1000;i++)
for(j=1;j*i*i<=1000000;j++)
vis[j*i*i]=1;
for(i=1;i<=1000000;i++)
if(!vis[i])a[++a[0]]=i;
scanf("%d",&t);
while(t--){
scanf("%d",&k);
printf("%d\n",a[k]);
}
return 0;
}
2.bzoj 2301 //2301: [HAOI2011]Problem b //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2301
//2301: [HAOI2011]Problem b
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2301
//先编写朴素算法
//50000*50000=2.5*10^9 int 要溢出,故采用long long
//样例通过,以下为 朴素算法,但不能AC.算法的时间复杂度为n*b*d*logk=50000^3*16=125*16*10^12=2*10^15超时无疑 2019-7-7 16:10
//1<=x<=b,1<=y<=d 最大公约数为k的数量计算f(b,d)=[b/k]*[d/k]
//根据 容斥原理 结果为f(b,d)-f(a-1,d)-f(c-1,b)+f(a-1,c-1)
//输出不对
//针对数据2
//1 5 1 5 2
//(2,2),(2,4),(4,2) (5/2)*(5/2)=4 (2,2),(2,4),(4,2),(4,4)如何去除(4,4)
//翻看之前https://blog.youkuaiyun.com/mrcrack/article/details/86929213博客,很受启发2019-7-11 16:32
//从题解来说,此文写得很棒https://blog.youkuaiyun.com/outer_form/article/details/50590197
//遇到 浮点数例外 if(!(i%prime[j]))break;//此处写成 if(!i%prime[j])break; 出现了 浮点数例外
//漏了此句return ans;//漏了此句return ans;查了好久。2019-7-12 22:09
//样例通过,提交AC.2019-7-12 22:11
#include <stdio.h>
#include <string.h>
#define maxn 50010
#define LL long long
LL prime[maxn],not_prime[maxn],mu[maxn],sum[maxn];
void linear_shaker(LL x){
LL i,j;
memset(not_prime,0,sizeof(not_prime)),memset(mu,0,sizeof(mu)),mu[1]=1,sum[0]=0,sum[1]=1,prime[0]=0;//漏了此句prime[0]=0
for(i=2;i<=x;i++){
if(!not_prime[i])prime[++prime[0]]=i,mu[i]=-1;
for(j=1;prime[j]*i<=x;j++){
not_prime[prime[j]*i]=1;//漏了此句 not_prime[prime[j]*i]=1;
if(!(i%prime[j]))break;//此处写成 if(!i%prime[j])break; 出现了 浮点数例外
mu[prime[j]*i]=-mu[i];//此处写成not_prime[prime[j]*i]=1,mu[prime[j]*i]=-mu[i];
}
sum[i]=sum[i-1]+mu[i];
}
}
LL min(LL a,LL b){
return a<b?a:b;
}
LL f(LL a,LL b,LL k){
LL i,last,t,ans=0;
a/=k,b/=k;
t=min(a,b);
for(i=1;i<=t;i=last+1){
last=min(a/(a/i),b/(b/i));
ans+=(sum[last]-sum[i-1])*(a/i)*(b/i);//ans+=(sum[last]-sum[i-1])*(a/last)*(b/last);
}
return ans;//漏了此句return ans;
}
int main(){
LL n,a,b,c,d,k,ans;
scanf("%lld",&n);
linear_shaker(50000);
while(n--){
scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
ans=f(b,d,k)-f(a-1,d,k)-f(c-1,b,k)+f(a-1,c-1,k);
printf("%lld\n",ans);
}
return 0;
}
//2301: [HAOI2011]Problem b
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2301
//先编写朴素算法
//50000*50000=2.5*10^9 int 要溢出,故采用long long
//样例通过,以下为 朴素算法,但不能AC.算法的时间复杂度为n*b*d*logk=50000^3*16=125*16*10^12=2*10^15超时无疑 2019-7-7 16:10
//
//
#include <stdio.h>
#define LL long long
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
int main(){
int n,a,b,c,d,k,x,y;
LL cnt;
scanf("%d",&n);
while(n--){
cnt=0;
scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
for(x=a;x<=b;x++)
for(y=c;y<=d;y++)
if(gcd(x,y)==k)
cnt++;
printf("%lld\n",cnt);
}
return 0;
}
3.bzoj 2820 //P2257 YY的GCD //在线测评地址https://www.luogu.org/problemnew/show/P2257
//P2257 YY的GCD
//在线测评地址https://www.luogu.org/problemnew/show/P2257
//该题与bzoj 2301有何不同,还是在于N,M<=10^7按bzoj 2301算法,超时可能性很大
//重新读题,才发现最大公约数为2,3,5,7,等等,而不是1,看来一开始还是误读了。
//https://www.luogu.org/problemnew/solution/P2257 作者: Mzwuzad 更新时间: 2018-03-23 09:31此文思路写得不错
//样例通过,不放心int,测试了
//1 10000000 10000000
//输出1265524029
//提交50分,测试点6-10WA基本可确认还是int溢出的问题
//重新测试1 10000000 10000000
//输出27035327805
//还是要小心些。
//将相关int改成long long,提交50分,测试点6-10WA。2019-7-15 8:42
//对比AC代码,发现ans+=(sum[last]-sum[i-1])*(n/i)*(m/i);//此处写成(n/i)*(m/i)*(sum[last]-sum[i-1]);
//重新测试1 10000000 10000000
//输出27493351185725
//提交AC,该题还是在数据溢出问题上,折腾了不少时间。2019-7-15 8:56
#include <stdio.h>
#include <string.h>
#define maxn 10000010
#define LL long long
int not_prime[maxn],prime[maxn/10],mu[maxn];
LL sum[maxn];
void linear_shaker(int x){
int i,j;
memset(not_prime,0,sizeof(not_prime)),memset(mu,0,sizeof(mu)),mu[1]=1;
for(i=2;i<=x;i++){
if(!not_prime[i])prime[++prime[0]]=i,mu[i]=-1;
for(j=1;prime[j]*i<=x;j++){
not_prime[prime[j]*i]=1;
if(!(i%prime[j]))break;
mu[prime[j]*i]=-mu[i];
}
}
memset(sum,0,sizeof(sum));
for(i=1;i<=prime[0];i++)
for(j=prime[i];j<=x;j+=prime[i])
sum[j]+=mu[j/prime[i]];
for(i=1;i<=x;i++)sum[i]+=sum[i-1];
}
int min(int a,int b){
return a<b?a:b;
}
LL cal(int n,int m){
int i,last,t;
LL ans=0;
t=min(n,m);
for(i=1;i<=t;i=last+1){
last=min(n/(n/i),m/(m/i));
ans+=(sum[last]-sum[i-1])*(n/i)*(m/i);//此处写成(n/i)*(m/i)*(sum[last]-sum[i-1]);
}
return ans;
}
int main(){
int t,n,m;
scanf("%d",&t);
linear_shaker(10000000);
while(t--){
scanf("%d%d",&n,&m);
printf("%lld\n",cal(n,m));
}
return 0;
}
4.bzoj 3529 //3529: [Sdoi2014]数表 //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3529
//3529: [Sdoi2014]数表
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3529
//模2^31 int溢出 采用long long
//整除 看了半天才明白,b整除a,是指b是a的约数
//样例1中,第1组数据解释如下
1 1 1 1
1 1+2 1 1+2
1 1 1+3 1
1 1+2 1 1+2+4
不大于3的数据和如下
1 1 1 1
1 1+2 1 1+2
1 1 1
1 1+2 1
和为
4+8+3+5=20
//至此,样例看懂
//https://blog.youkuaiyun.com/Regina8023/article/details/44243057此文思路及代码值得一读
//在linux下测试,整数的自然溢出,
noilinux@ubuntu:~/program/bzoj/3529$ ./3529
2147483648
2147483647
noilinux@ubuntu:~/program/bzoj/3529$ ./3529
2147483647
2147483647
noilinux@ubuntu:~/program/bzoj/3529$ ./3529
2147483649
2147483647
//突然想到,确实是有问题的2019-7-19 07:56
//回到win7,测试了int的自然溢出,以及处理手法,代码如下
#include <stdio.h>
int main(){
int a;
while(1){
scanf("%d",&a);
printf("%d\n",a);//自然溢出
printf("%d\n",a&0x7fffffff);//去除符号位的影响。使输出结果均为正数。
}
return 0;
}
//测试过程如下,
2147483648
-2147483648
0
2147483647
2147483647
2147483647
2147483649
-2147483647
1
2147483650
-2147483646
2
//有收获2019-7-19 8:10
//编写过程中,发现 莫比乌斯函数的计算还是不熟练,
//造成了编码的问题if(!not_prime[i])prime[++prime[0]]=i,mu[i]=-1;//此处写成if(!not_prime[i])prime[++prime[0]]=i;
//样例通过,2019-7-19 9:20
//提交AC,2019-7-19 9:24
//算法 莫比乌斯反演+树状数组 离线查询
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define M 100000
struct node1{
int n,m,a,seq;
}q[20010];
struct node2{
int v,seq;
}f[M];
int not_prime[M+5],prime[M],mu[M+5],c[M+5],ans[20010];
int cmp1(node1 a,node1 b){
return a.a<b.a;
}
int cmp2(node2 a,node2 b){
return a.v<b.v;
}
void linear_shaker(int x){//线性筛
int i,j;
memset(not_prime,0,sizeof(not_prime)),memset(mu,0,sizeof(mu)),mu[1]=1,prime[0]=0;
for(i=2;i<=x;i++){
if(!not_prime[i])prime[++prime[0]]=i,mu[i]=-1;//此处写成if(!not_prime[i])prime[++prime[0]]=i;
for(j=1;prime[j]*i<=x;j++){
not_prime[prime[j]*i]=1;
if(!(i%prime[j]))break;
mu[prime[j]*i]=-mu[i];
}
}
}
void getf(int x){
int i,j;
memset(f,0,sizeof(f));
for(i=1;i<=x;i++)
for(j=i;j<=x;j+=i)
f[j].v+=i;
for(i=1;i<=x;i++)f[i].seq=i;
sort(f+1,f+1+x,cmp2);
}
int lowbit(int x){
return x&-x;
}
void update(int k,int delta,int n){
while(k<=n)c[k]+=delta,k+=lowbit(k);
}
int get_sum(int k){
int ans=0;
while(k>0)ans+=c[k],k-=lowbit(k);
return ans;
}
int min(int a,int b){
return a<b?a:b;
}
int get_ans(int n,int m){
int i,j,last,t,ans=0;
t=min(n,m);
for(i=1;i<=t;i=last+1){
last=min(n/(n/i),m/(m/i));
ans+=(n/i)*(m/i)*(get_sum(last)-get_sum(i-1));
}
return ans&0x7fffffff;//消除int中符号位的影响,使输出结果为非负数.
}
int main(){
int t,i,j,k;
linear_shaker(M),getf(M);
scanf("%d",&t);
for(i=1;i<=t;i++)scanf("%d%d%d",&q[i].n,&q[i].m,&q[i].a),q[i].seq=i;
sort(q+1,q+1+t,cmp1);//此处写成sort(q+1,q+1+t);//按a自小到大排序.
memset(c,0,sizeof(c)),memset(ans,0,sizeof(ans));
for(i=1,j=1;i<=t;i++){
for(;j<=M&&f[j].v<=q[i].a;j++)
for(k=f[j].seq;k<=M;k+=f[j].seq)
update(k,f[j].v*mu[k/f[j].seq],M);//涉及单点更新要影响整个前缀和,故采用树状数组
ans[q[i].seq]=get_ans(q[i].n,q[i].m);
}
for(i=1;i<=t;i++)printf("%d\n",ans[i]);
return 0;
}
5.bzoj 2154 //2154: Crash的数字表格 //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2154
//2154: Crash的数字表格
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2154
//此文https://www.cnblogs.com/zj75211/p/8270613.html思路清晰,值得一读,摘抄如下



//样例通过,提交Memory_Limit_Exceed,测算了一下
//long long 4*8*10^7/1024/1024=305MB确实超出内存限制
//改成int 4*4*10^7/1024/1024=153MB
//开始动手将long long 改成int
//样例通过,提交Wrong_Answer 2019-7-21 17:49
//ans=((1ll)*ans+(1ll)*(pmu[last]-pmu[i-1])*sum(n/i,m/i))%mod;//此处写成ans=(ans+(1ll)*(pmu[last]-pmu[i-1])*sum(n/i,m/i))%mod;
//ans=((1ll)*ans+((1ll)*(i+last)%mod*(last-i+1)/2%mod*F(n/i,m/i)%mod))%mod;//此处写成ans=(ans+((1ll)*(i+last)%mod*(last-i+1)/2%mod*F(n/i,m/i)%mod))%mod;
//提交Wrong_Answer 2019-7-21 17:52
//ans=((1ll)*ans+(1ll)*(pmu[last]-pmu[i-1])*sum(n/i,m/i)%mod)%mod;//此处写成ans=((1ll)*ans+(1ll)*(pmu[last]-pmu[i-1])*sum(n/i,m/i))%mod;
//return (1ll)* (1+n)*n%mod*(1+m)%mod*m%mod/4;//此处写成return (1ll)* (1+n)*n%mod*(1+m)*m%mod/4;
//提交Wrong_Answer 2019-7-21 18:06
//ans=((1ll)*ans+((1ll)*(i+last)*(last-i+1)/2%mod*F(n/i,m/i)%mod))%mod;//此处写成ans=((1ll)*ans+((1ll)*(i+last)%mod*(last-i+1)/2%mod*F(n/i,m/i)%mod))%mod;
//return (1ll)* (1+n)*n/2%mod*((1ll)*(1+m)*m/2%mod)%mod;//此处写成(1ll)* (1+n)*n%mod*(1+m)%mod*m%mod/4;
//提交AC.2019-7-21 18:12
//该题在 模运算中最大的问题 是 要小心 除法,除法是模运算中需要注意的问题.2019-7-21 18:14
//此文https://blog.youkuaiyun.com/VictoryCzt/article/details/85054670推导写得不错,值得一看 2019-7-24 8:05


#include <stdio.h>
#include <string.h>
#define maxn 10000010
#define mod 20101009
int not_prime[maxn],prime[maxn/10],mu[maxn],pmu[maxn];
void linear_shaker(int x){
int i,j;
memset(not_prime,0,sizeof(not_prime)),memset(mu,0,sizeof(mu)),mu[1]=1,pmu[0]=0,pmu[1]=1,prime[0]=0;
for(i=2;i<=x;i++){
if(!not_prime[i])prime[++prime[0]]=i,mu[i]=-1;
for(j=1;prime[j]*i<=x;j++){
not_prime[prime[j]*i]=1;
if(!(i%prime[j]))break;
mu[prime[j]*i]=-mu[i];
}
pmu[i]=(pmu[i-1]+(1ll)*mu[i]*i%mod*i%mod)%mod;
}
}
int min(int a,int b){
return a<b?a:b;
}
int sum(int n,int m){
return (1ll)* (1+n)*n/2%mod*((1ll)*(1+m)*m/2%mod)%mod;//此处写成(1ll)* (1+n)*n%mod*(1+m)%mod*m%mod/4;//此处写成return (1ll)* (1+n)*n%mod*(1+m)*m%mod/4;
}
int F(int n,int m){
int i,t,last,ans=0;
t=min(n,m);
for(i=1;i<=t;i=last+1){
last=min(n/(n/i),m/(m/i));
ans=((1ll)*ans+(1ll)*(pmu[last]-pmu[i-1])*sum(n/i,m/i)%mod)%mod;//此处写成ans=((1ll)*ans+(1ll)*(pmu[last]-pmu[i-1])*sum(n/i,m/i))%mod;//此处写成ans=(ans+(1ll)*(pmu[last]-pmu[i-1])*sum(n/i,m/i))%mod;
}
return ans;
}
int main(){
int n,m,i,last,t,ans=0;
scanf("%d%d",&n,&m);
t=min(n,m);
linear_shaker(t);//漏了此句
for(i=1;i<=t;i=last+1){
last=min(n/(n/i),m/(m/i));
ans=((1ll)*ans+((1ll)*(i+last)*(last-i+1)/2%mod*F(n/i,m/i)%mod))%mod;//此处写成ans=((1ll)*ans+((1ll)*(i+last)%mod*(last-i+1)/2%mod*F(n/i,m/i)%mod))%mod;//此处写成ans=(ans+((1ll)*(i+last)%mod*(last-i+1)/2%mod*F(n/i,m/i)%mod))%mod;
}
printf("%d\n",(ans+mod)%mod);
return 0;
}
6.bzoj 2693 //bzoj 2693 jzptab
//因该题是bzoj权限题,普通用户无法看到该题,若能将bzoj 2154: Crash的数字表格 尽可能优化,也能达到
//bzoj 2693 jzptab的效果,故采用如下测评地址 2019-7-22 10:48
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2154
//bzoj 2693 jzptab
//因该题是bzoj权限题,普通用户无法看到该题,若能将bzoj 2154: Crash的数字表格 尽可能优化,也能达到
//bzoj 2693 jzptab的效果,故采用如下测评地址 2019-7-22 10:48
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2154
//此文https://www.cnblogs.com/nlKOG/p/10543409.html思路值得一读


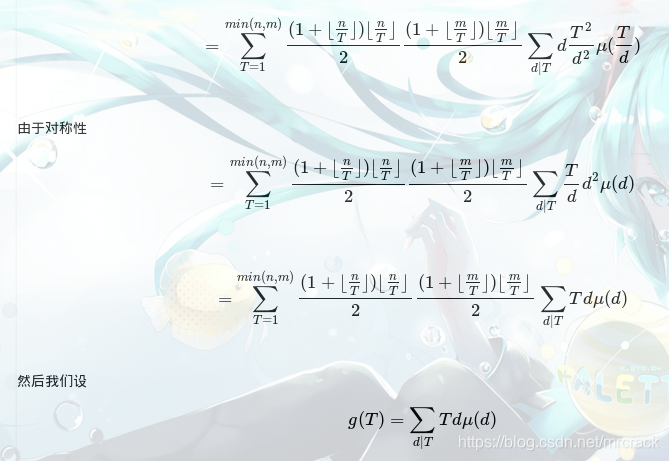


//
//
//
//





 本文详细解析了莫比乌斯反演在算法竞赛中的应用,通过具体题目讲解了如何利用这一数学工具解决复杂问题,包括完全平方数计数、最大公约数统计等,深入探讨了算法细节与优化策略。
本文详细解析了莫比乌斯反演在算法竞赛中的应用,通过具体题目讲解了如何利用这一数学工具解决复杂问题,包括完全平方数计数、最大公约数统计等,深入探讨了算法细节与优化策略。
















 165
165

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








