前文我们简述了 二叉树遍历之递归遍历
其实用到的是递归中自己的栈来完成的,那么我们要是用迭代的话也是要通过自己的栈来完成
前序遍历:根 左 右
我们在递归遍历时通过前序遍历的原理图示展示了整个过程:
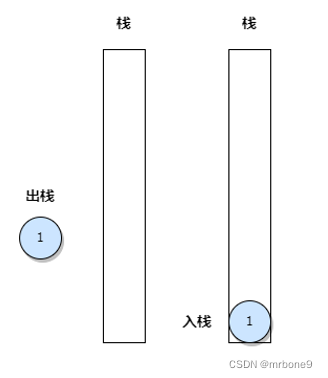
根节点第一次出栈就可以打印了,然后再来分别出栈左右子节点
void preorderIteration(struct TreeNode* root, MyStack *stk)
{
if(root == NULL)
return;
myStackPush(stk, root);
while( ! myStackEmpty(stk) )
{
root = myStackTop(stk);
myStackPop(stk);
printf("val=%d\n", root->val);
if(root->right)
myStackPush(stk, root->right);
if(root->left)
myStackPush(stk, root->left);
}
}中序遍历:左 根 右
我们遇见左节点时还要看有没有左子节点,一直要到最左边的叶子为止
所以根节点先入栈,然后持续对左子节点压栈,直到左子节点为NULL,这个时候就可以出栈左子节点,打印其值
左边节点值打印完成,如果其没有右子节点,那么再出栈的话就是其父节点(根)
如果有右子节点,那么该左节点视为子树的根节点,对右子树进行重复逻辑
void inorderIteration(struct TreeNode* root, MyStack *stk)
{
if(root == NULL)
return;
while(! myStackEmpty(stk) || root != NULL)
{
if(root != NULL)
{
myStackPush(stk, root);
root = root->left;
}
else
{
root = myStackTop(stk);
myStackPop(stk);
printf("val=%d\n", root->val);
root = root->right;
}
}
}1. 依次入栈根,左子节点,直到没有左子节点
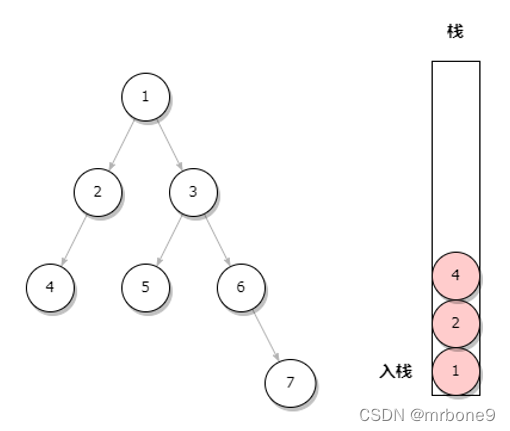
2. 出栈,节点 4 没有右子节点,再出栈就是其父节点 2,同样节点 2也没有右子节点,再出栈就是节点 1
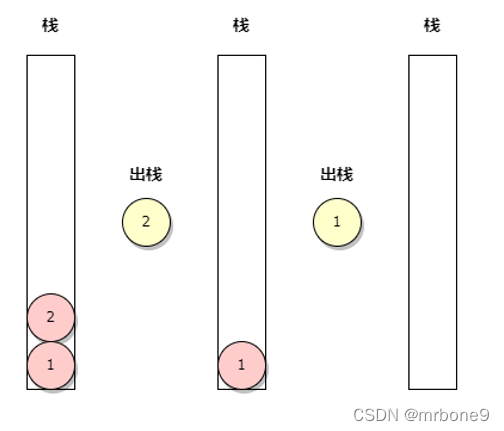
3. 节点 1 有 右子节点,那么就开始处理右子树,整个过程逻辑一样

后序遍历:左,右,根
与前面两种方式不一样,我们在处理完左树后,根节点还不能打印
除非根节点没有右子树,或者右子树已经被打印了,才能打印根节点
所以根节点会进行二次入栈,当第二次出栈的时候通过比较临时节点变量(保存压栈时的根节点)与当前根节点是否一样,一样表示已经处理完,这个时候就能够打印当前根节点
void postorderIteration(struct TreeNode* root, MyStack *stk)
{
if(root == NULL)
return;
struct TreeNode* prev = NULL;
while(! myStackEmpty(stk) || root != NULL)
{
while(root != NULL)
{
myStackPush(stk, root);
root = root->left;
}
root = myStackTop(stk);
myStackPop(stk);
if(root->right == NULL || root->right == prev)
{
printf("val=%d\n", root->val);
prev = root;
root = NULL;
}
else
{
myStackPush(stk, root);
root = root->right;
}
}
}1. 根节点开始压栈,完成左子节点的压栈
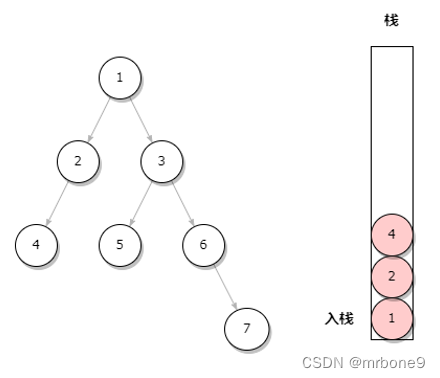
2. 出栈,节点 4 没有右子节点,可以打印值,继续出栈节点 2,也没有右子节点打印值
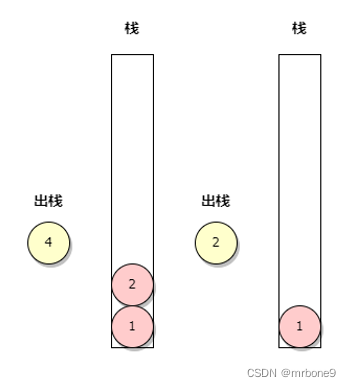
3. 节点 1 出栈后发现右右子节点,并且右子节点还未处理,第二次压栈
4. 处理节点 1 的右子树,逻辑一样。节点 3 同样进行了 二次压栈
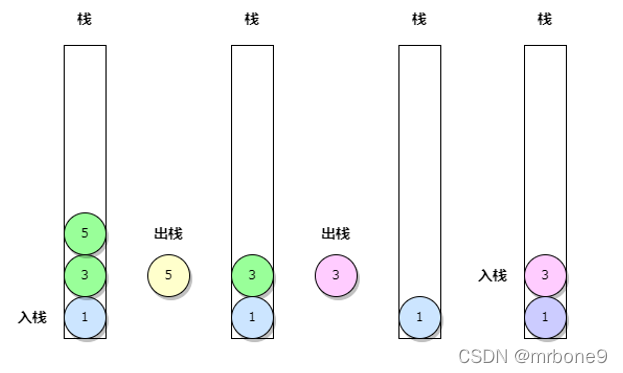
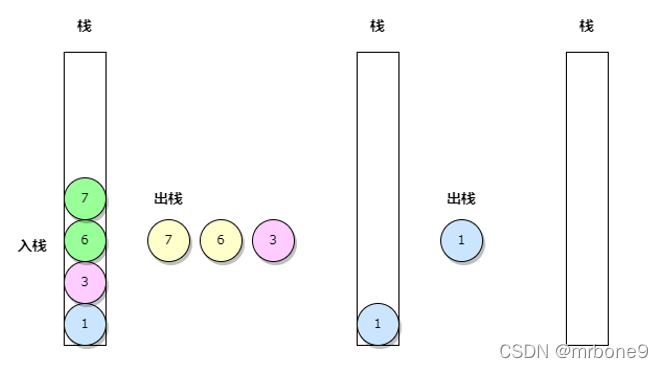
5. 继续处理右子节点直至完成后才可以打印 根节点






















 772
772

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








