数学建模系列--拟合算法

一.拟合与插值算法的比较

• 前者追求’简‘，牺牲了一点准确性，不过也保证了误差足够小。后者追求准确性（数据量大时，有龙格现象，n很大时计算量特别大）但是精度高。
• 不同于插值算法，不要求函数过all已知点，与原数据点接近即可。
• eg 对于线性拟合，当n阶数越大，RRE误差平方和越小，拟合优度R²越大，代价是计算量大了，且相对于1阶的拟合，R²提高不大，所以综合考虑下，大多选择线性拟合。

二.基础知识

1.拟合算法的用途？

用来预测，对于数目较大的、自然发展的、没有剧烈变动的事物进行预测，把握事物发展方向。

2.最小二乘法

• 残差：表示测量值和预测值之差
• 为什么我们最小化残差的平方和呢？为什么不是绝对值之和？或者四次方之和？
  最直接的原因是平方操作不显著增加多项式次数，且处处可导。相比之下，绝对值操作在原点不可导，四次方阶数太高，不易求解。

3.龙格现象

• 龙格现象（Runge）指的是对于某些函数，使用均匀节点构造高次多项式差值时，在插值区间的边缘的误差可能很大的现象。. 它是由Runge在研究多项式差值的误差时发现的，这一发现很重要，因为它表明，并不是插值多项式的阶数越高，效果就会越好。
• 参考文献：龙格现象(Runge Phenomenon) - 知乎 (zhihu.com)

4.数理统计-假设检验

• 原假设H0和备则假设H1的设立标准
  • 原假设是在一次试验中有绝对优势出现的事件，而备择假设在一次试验中不易发生(或几乎不可能发生)的事件。因此，在进行单侧检验时，最好把原假设取为预想结果的反面，即把希望证明的命题放在备择假设上。
  • 原假设的设法则根据题目要求做出假设，且必须保证等号放在原假设。
  • 一般研究者希望原假设能够被拒绝，备择假设能够被接受，但若没有充分理由证明原假设错误，就不能够轻易拒绝原假设。
  • 在假设检验中，一方面原假设受到保护，不能够被轻易拒绝，处于有利地位。另一方面就算原假设被接受，也仅能说明拒绝它的理由不够充分，而不意味着原假设必然正确。
• 将数据代入统计量中得到的值为检测值t，检测值对应的p值含义是P(X>t)-概率 计算公式为p=1-φ(u) ，双侧检验p为单侧的两倍，将p值与显著性水平u对比，若p>u，则落在接受域内-接受原假设，反之亦然。
  • MATLAB实现---Z检验（已知总体方差）--normcdf计算标正累计密度函数，可求出P(X<t)。
  • 未知总体方差--t检验（未知总体方差）--tcdf计算标正累计密度函数，可求出P(X<t)。
    数模比赛中使用较多

• 三.MATLAB实现拟合

法1.利用MATLAB代码求解

• 代码-算法
  • 1.先画出原有数据点的散点图，hold on 在此基础上画出拟合图，方便观察
  • 2.利用最小二（mean 二次）乘法求解未知参数K b，然后代入拟合曲线方程即可
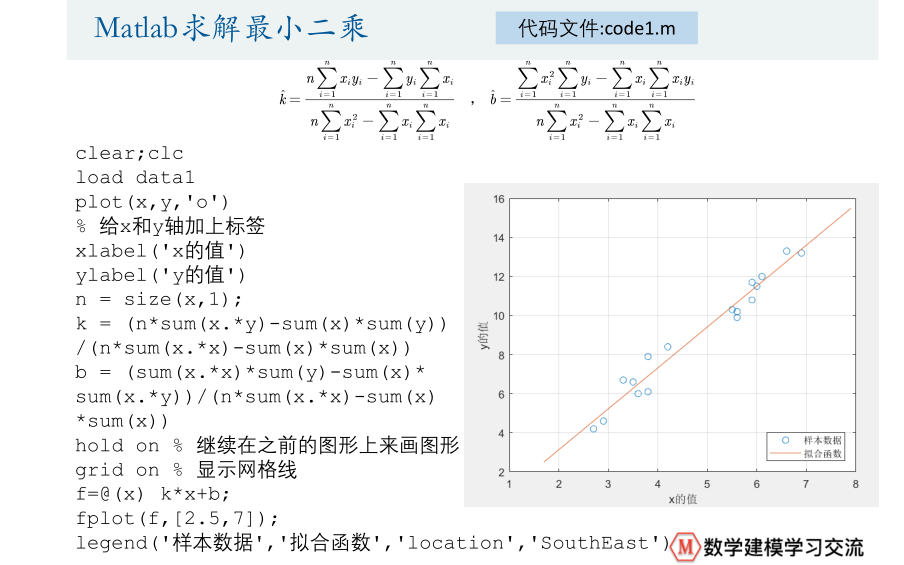
  • 3.对拟合结果进行评估-计算R²
    • 代码-算法

利用MATLAB求解出拟合函数中未知参数：k、b之后，我们就可以画出拟合函数的图像，并且与之前由样本点构成的散点图进行观察分析，可以发现拟合程度很好。

但是我们需要计算拟合优度R²来分析拟合的好与坏，用上图所示算法计算出R²，由于这里我们的拟合函数是线性函数，所以可以根据R²大小来评价拟合结果，拟合优度R² 【0,1】越大越好。

注意：上述的线性函数并非传统意义的线性函数，可以先看下图清风老师的课件来理解一下

• 
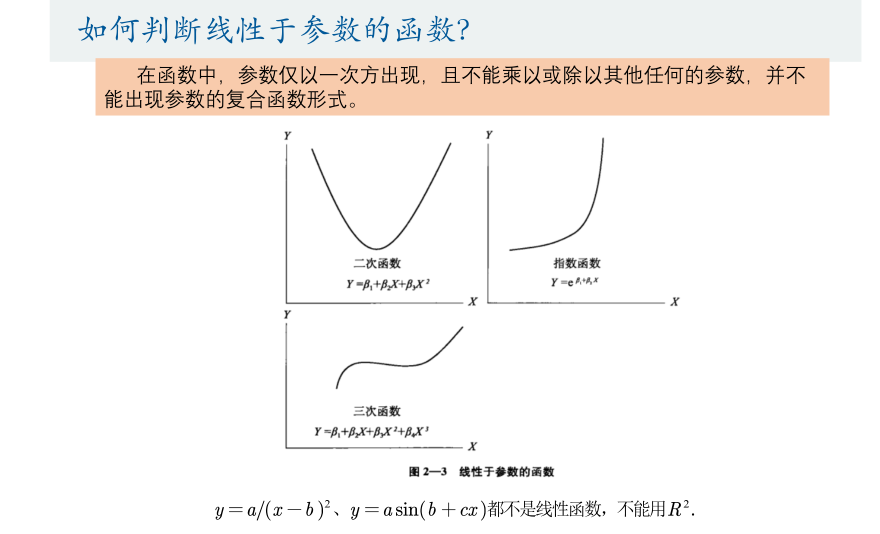
  此处线性函数并非传统的线性函数，这里的线性指的是线性于参数并非变量线性，eg:y=a+bx²为线性函数，而下面的函数X（t）为非线性于参数的函数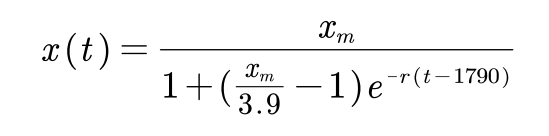

对于拟合函数为非线性于参数的情况下：根据误差平方和SSE判定优劣，越小越好

法2.利用MATLAB自带的曲线拟合工具箱-curve fitting

法1是利用最小二乘法求解拟合函数，需要我们敲代码来实现，但是MATLAB有个自带的工具箱，也可以实现拟合算法，不需要我们敲代码！