Harris角点检测

1.实验基础

本实验将从纹理平坦、垂直或水平边缘多、纹理角点丰富三个场景的图片各五张不同角度（正面、侧面、远近、旋转、明暗）等角度进行对比。

1.1角点概述

如果某一点在任意方向的一个微小变动都会引起灰度很大的变化，那么我们就把它称之为角点’
关于角点的具体描述可以有几种：
1、一阶导数（即灰度的梯度）的局部最大所对应的像素点
2、两条及两条以上边缘的点
3、图像中的梯度值和梯度方向的变化速率都很高的点
4、角点处的一阶导数最大，二阶导数为0，指示物体边缘变化不连续的方向

1.2角点检测基本原理

当一个窗口在图像上移动，在平滑区域如图(a)，窗口在各个方向上没有变化。在边缘上如图(b)，窗口在边缘的方向上没有变化。在角点处如图©，窗口在各个方向上具有变化。Harris角点检测正是利用了这个直观的物理现象，通过窗口在各个方向上的变化程度，决定是否为角点。

将图像窗口平移[u,v]产生灰度变化E(u,v)

可得到：

对于局部微小的移动量 [u,v]，近似表达为：

其中M是 2*2 矩阵，可由图像的导数求得：

E(u,v)的椭圆形式如下图：

定义角点响应函数 R 为：

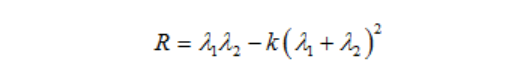
Harris角点检测算法就是对角点响应函数R进行阈值处理：R > threshold，即提取R的局部极大值。

1.3Harris角点检测代码

# -*- coding: utf-8 -*-
from pylab import *
from PIL import Image
from PCV.localdescriptors import harris
"""
Example of detecting Harris corner points (Figure 2-1 in the book).
"""
# 读入图像
im = array(Image.open('../data/empire.jpg').convert('L'))
# 检测harris角点
harrisim = harris.compute_harris_response(im)
# Harris响应函数
harrisim1 = 255 - harrisim
figure()
gray()
#画出Harris响应图
subplot(141)
imshow(harrisim1)
print harrisim1.shape
axis('off')
axis('equal')
threshold = [0.01, 0.05, 0.1]
for i, thres in enumerate(threshold):
    filtered_coords = harris.get_harris_points(harrisim, 6, thres)
    subplot(1, 4, i+2)
    imshow(im)
    print im.shape
    plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
    axis('off')
#原书采用的PCV中PCV harris模块
#harris.plot_harris_points(im, filtered_coords)
# plot only 200 strongest
# harris.plot_harris_points(im, filtered_coords[:200])
show()

在上面代码中，先打开一幅图像，将其转换成灰度图像，然后计算相响应函数，通过响应值选择角点。最后，将这些检测的角点在原图上显示出来。

2.场景一：纹理平坦

从左到右分别为正面、侧面、旋转、近处、亮处五张照片

2.1实验结果

正面

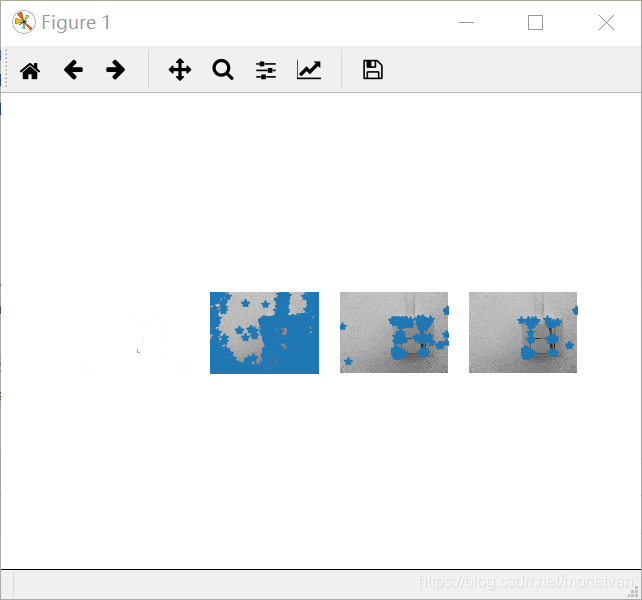
侧面

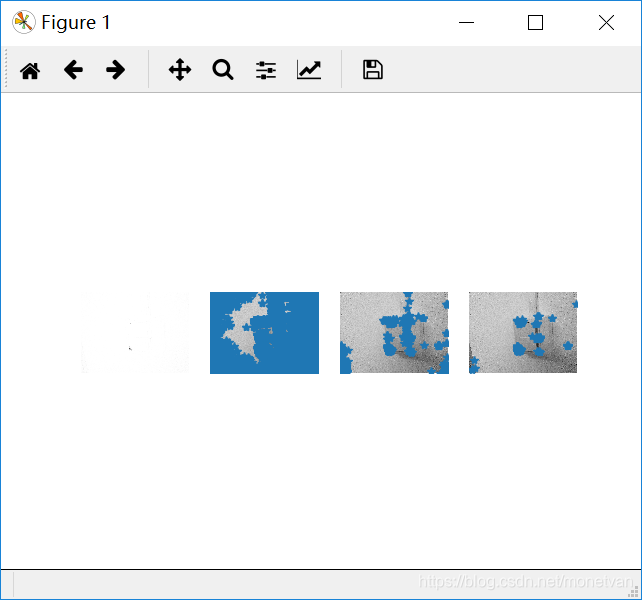
旋转

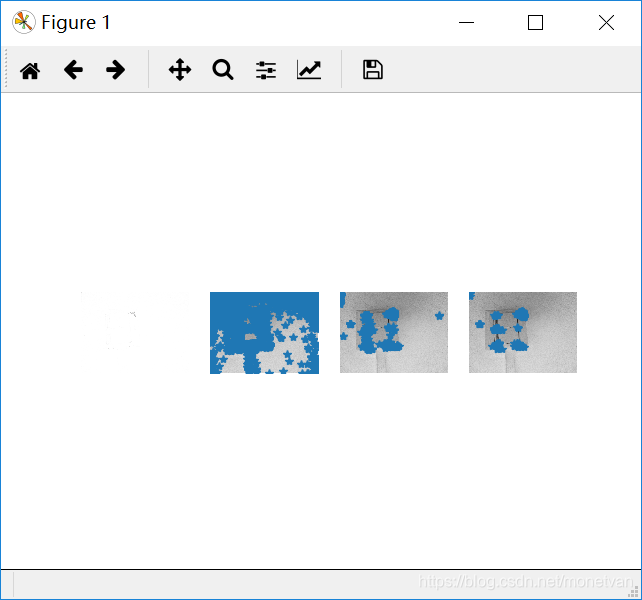
近处

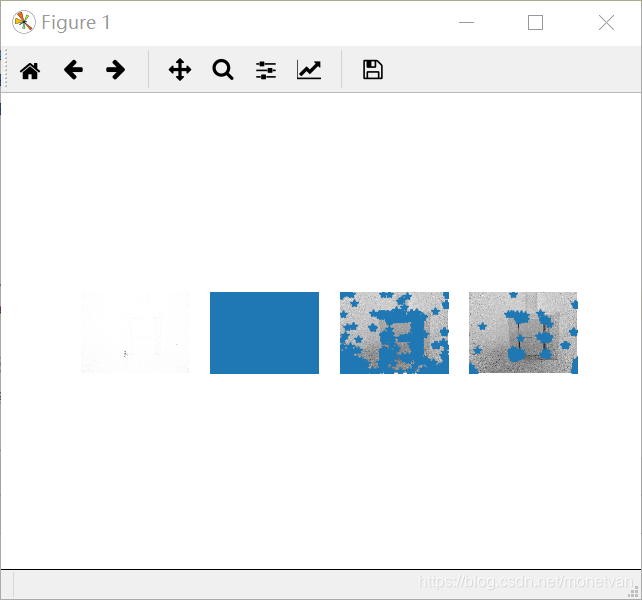
亮处

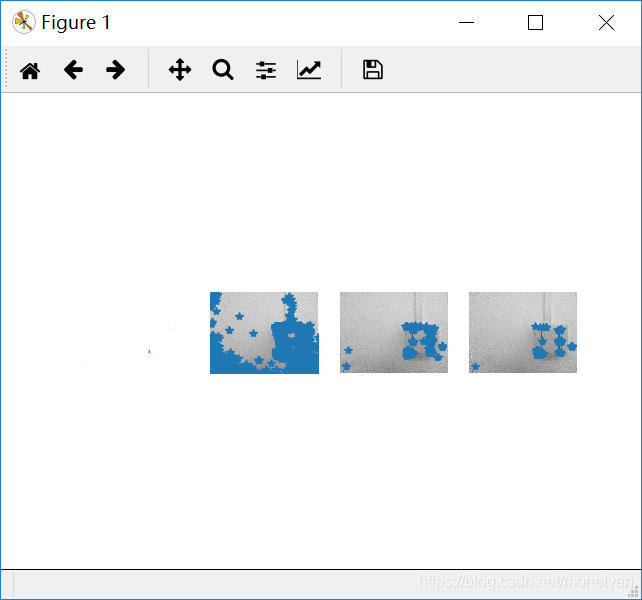
2.2结果分析

由这组实验可知，纹理平坦的图片角点较少。正面和侧面以及旋转后的图片角点基本一致，说明图片角度对纹理平坦的事物影响较小；近处拍摄的图片和其他图片相比，角点较多，说明图片远近对纹理平坦的事物有一定影响；亮处拍摄的图片相比较其他图片，初始角点较少，但通过函数运算后最终得到的角点数与前三张图片一致。总而言之，纹理平坦的图片的角点，对于图片角度、远近、明暗程度等因素的改变不敏感。

3.场景二：垂直或水平边缘多

从左到右分别是正面、侧面、旋转、远处、亮处五张照片

3.1实验结果

正面

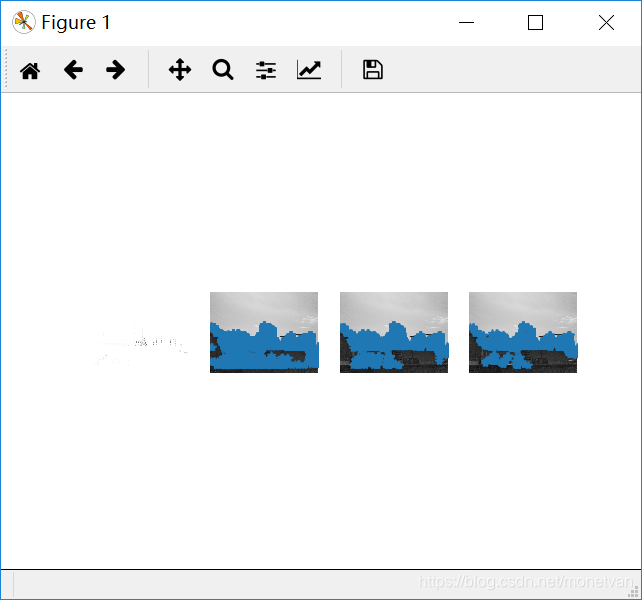
侧面

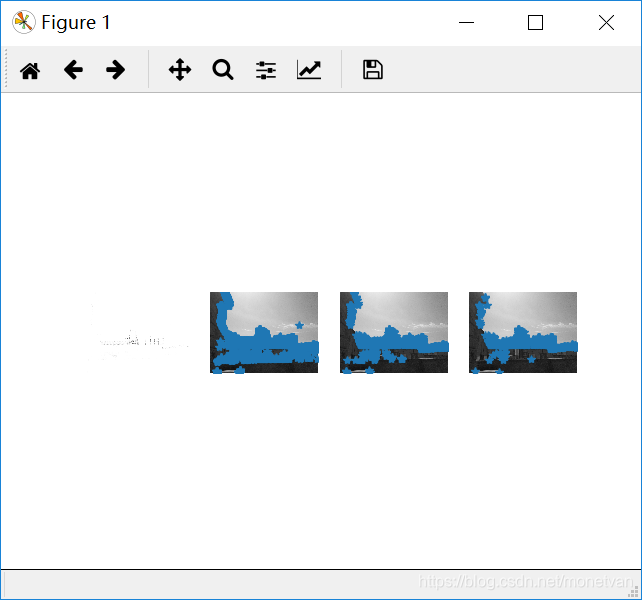
旋转

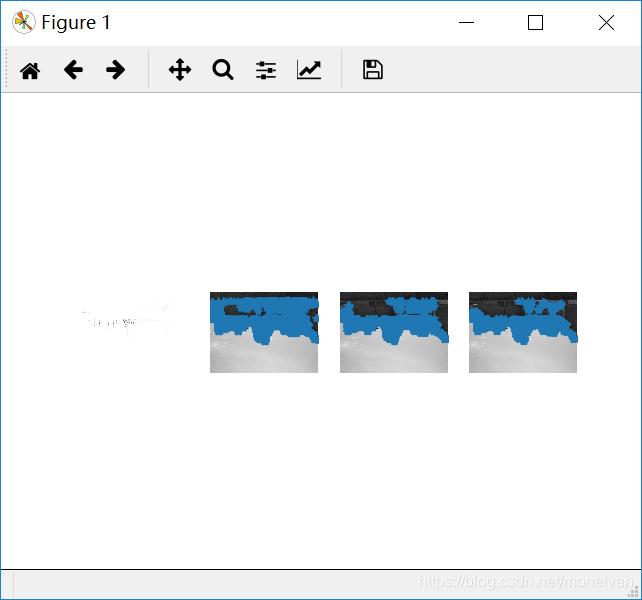
远处

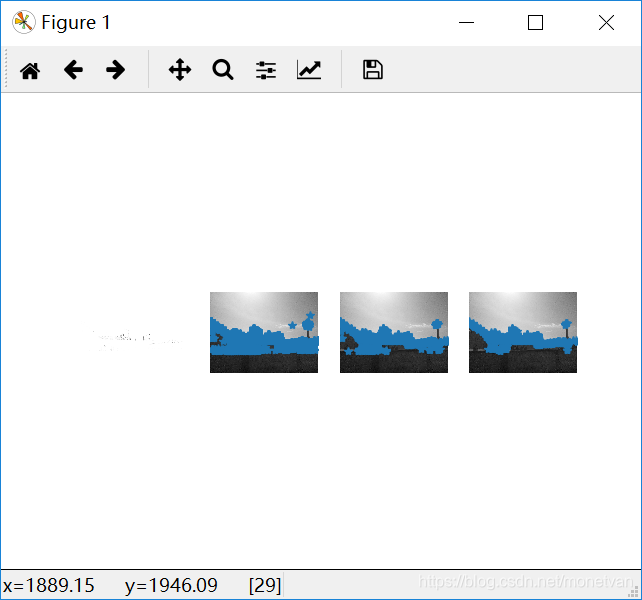
亮处

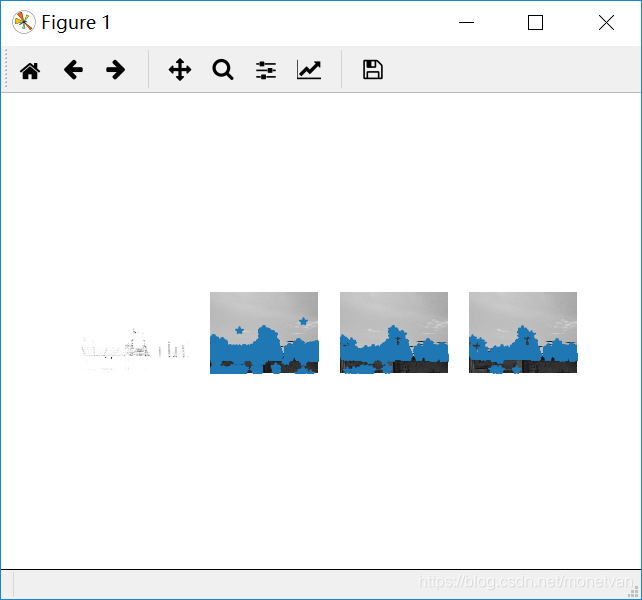
3.2结果分析

由这组实验可知，垂直或水平边缘多的图片角点较多。前四张图片的角点基本一致，说明图片角度和拍摄远近对垂直或水平边缘多的事物角点影响不大；亮处拍摄的图片相比较其他图片角点更多，说明明亮的图片有利于角点的寻找，图片明暗程度对角点有一定的影响。

4.场景三：纹理角点丰富

从左到右分别为正面、侧面、旋转、近处、暗处五张照片

4.1实验结果

正面

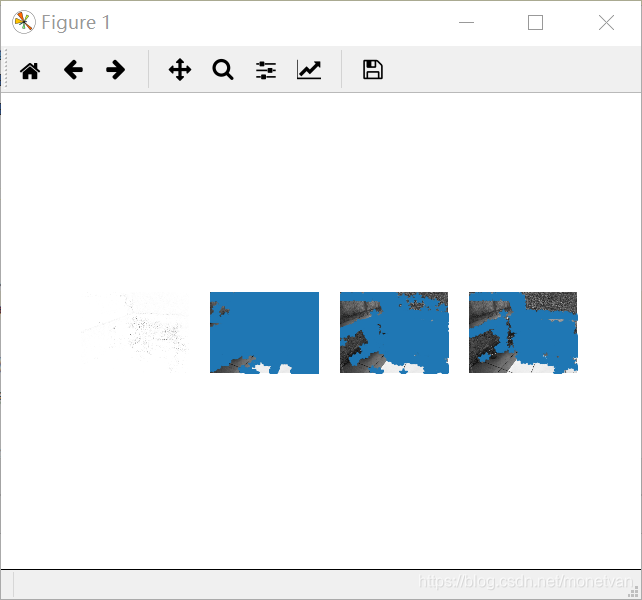
侧面

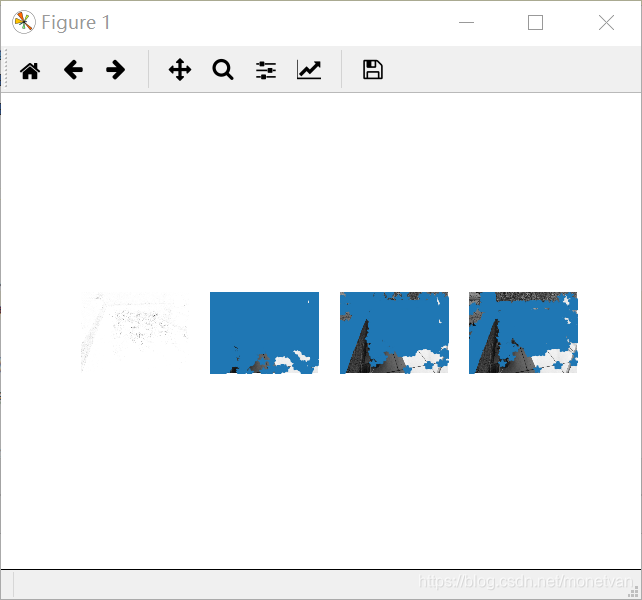
旋转

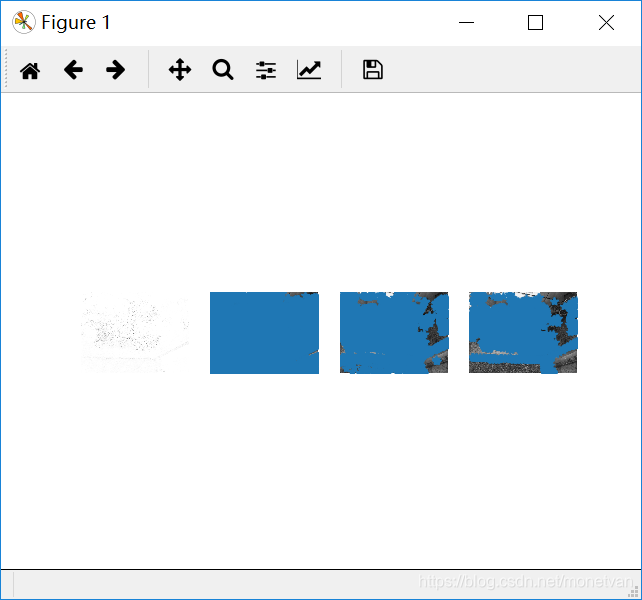
近处

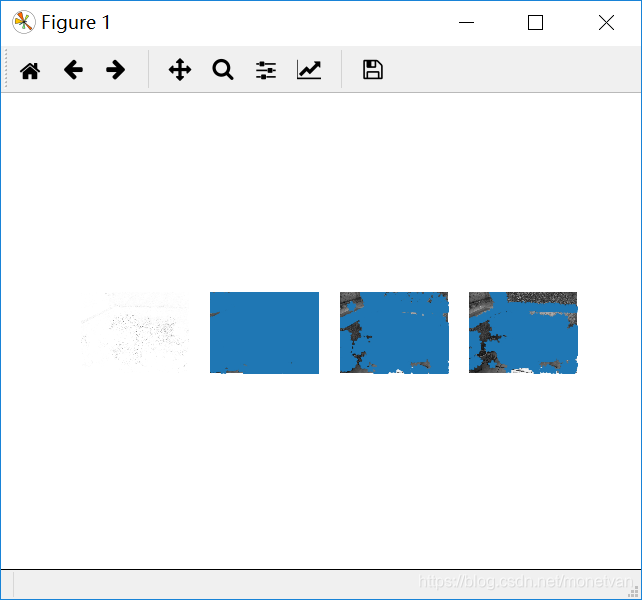
暗处

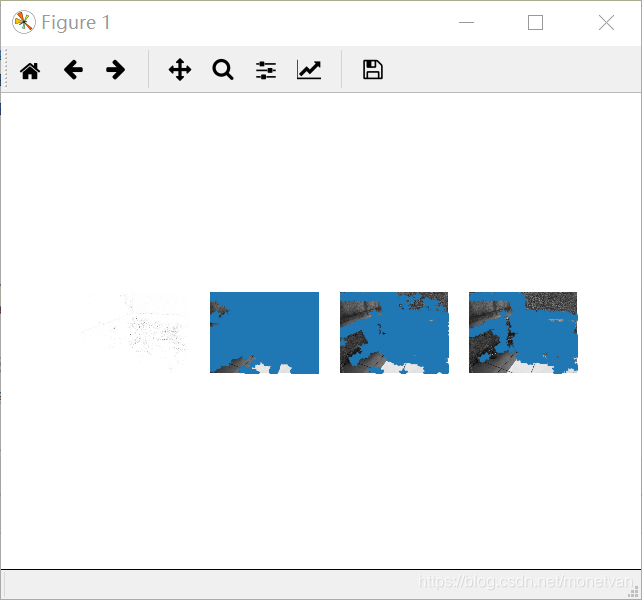
4.2结果分析

该组实验是三组中角点最多的一组，说明纹理丰富的图片角点多。正面和侧面以及旋转后的图片角点基本一致，说明图片角度对纹理丰富的事物影响不大；近处拍摄的图片和其他图片相比，角点较多，说明图片远近对纹理丰富的图片有一定影响；暗处拍摄的图片相比较其他图片，角点明显减少，说明亮度较低的图片不利于角点的寻找，明暗变化对纹理丰富的事物有一定影响。

5.实验总结

通过本次实验，我对harris角点检测有了一定的了解和认识，明白了角点检测的意义和实际用途，同时，也使我对于pycharm的运用更加熟练。
对比以上三组实验，可以得出harris角点检测算子具有旋转不变性，对于不同角度的照片，角点检测结果相差不大；不具有尺度不变性，图片尺寸改变会对结果造成影响；图片明暗改变也会对结果造成影响。