遗传算法

遗传算法

一、基本定义

遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。

二、实现过程

遗传算法的实现过程实际上就像自然界的进化过程那样。首先寻找一种对问题潜在解进行“数字化”编码的方案。（建立表现型和基因型的映射关系）然后用随机数初始化一个种群（那么第一批袋鼠就被随意地分散在山脉上），种群里面的个体就是这些数字化的编码。接下来，通过适当的解码过程之后（得到袋鼠的位置坐标），用适应性函数对每一个基因个体作一次适应度评估（袋鼠爬得越高，越是受我们的喜爱，所以适应度相应越高）。用选择函数按照某种规定择优选择（我们要每隔一段时间，在山上射杀一些所在海拔较低的袋鼠，以保证袋鼠总体数目持平。）。让个体基因变异（让袋鼠随机地跳一跳）。然后产生子代（希望存活下来的袋鼠是多产的，并在那里生儿育女）。遗传算法并不保证你能获得问题的最优解，但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解。（你不必去指导袋鼠向那边跳，跳多远。）而只要简单的“否定”一些表现不好的个体就行了。（把那些总是爱走下坡路的袋鼠射杀，这就是遗传算法的精粹！）

遗传算法的一般步骤：

1.评估每条染色体所对应个体的适应度。

2.遵照适应度越高，选择概率越大的原则，从种群中选择两个个体作为父方和母方。

3.抽取父母双方的染色体，进行交叉，产生子代。

4.对子代的染色体进行变异。

5.重复2，3，4步骤，直到新种群的产生。

结束循环。

三、编码表示

二进制编码

二进制编码是将原问题的结构变换成为染色体的位串结构。在二进制编吗中，首先要确定二进制字符串的长度l，该长度与变量的定义域和所求问题的计算精度有关。

实数编码

实数编码是将每个个体的染色体都用某一范围的一个实数（浮点数）来表示，其编码长度等于该问题变量的个数。这种编码方法是将问题的解空间映射到师叔空间上，然后在实数空间上进行遗传操作。实数编码适用于多维、高精度要求的连续函数优化问题。

四、代码实现

GA.m

% Optimizing a function  using Simple Genetic Algorithm with elitist preserved

%Max f(x1,x2)=100*(x1*x1-x2).^2+(1-x1).^2; -2.0480<=x1,x2<=2.0480


%下面为代码。函数最大值为3904.9262，此时两个参数均为-2.0480，有时会出现局部极值，此时一个参数为-2.0480，一个为2.0480。变
%异概率pm=0.05，交叉概率pc=0.8。

clc;clear all;

format long;%设定数据显示格式

%初始化参数

T=500;%仿真代数

N=10;% 群体规模

pm=0.05;pc=0.8;%交叉变异概率

umax=30;umin=-30;%参数取值范围

L=10;%单个参数字串长度，总编码长度Dim*L
Dim=20;%Dim维空间搜索

bval=round(rand(N,Dim*L));%初始种群，round函数为四舍五入

bestv=-inf;%最优适应度初值
funlabel=3;       %选择待优化的函数，1为Rastrigin,2为Schaffer,3为Griewank
Drawfunc(funlabel);%画出待优化的函数，只画出二维情况作为可视化输出

%迭代开始

for ii=1:T

%解码，计算适应度

    for i=1:N  %对每一代的第i个粒子
        for k=1:Dim
            y(k)=0;
            for j=1:1:L  %从1到L，每次加以1

               y(k)=y(k)+bval(i,k*L-j+1)*2^(j-1);%把第i个粒子转化为十进制的值，例如y1是第一维

            end 
            x(k)=(umax-umin)*y(k)/(2^L-1)+umin;%转化为实际的x1
        end

  %     obj(i)=100*(x1*x1-x2).^2+(1-x1).^2; %目标函数 
       obj(i)=fun(x,funlabel);
       xx(i,:)=x;

    end

    func=obj;%目标函数转换为适应度函数

    p=func./sum(func);

    q=cumsum(p);%累加

    [fmax,indmax]=max(func);%求当代最佳个体

   if fmax>=bestv

      bestv=fmax;%到目前为止最优适应度值

      bvalxx=bval(indmax,:);%到目前为止最佳位串

      optxx=xx(indmax,:);%到目前为止最优参数

   end   

   Bfit1(ii)=bestv; % 存储每代的最优适应度

%%%%遗传操作开始

%轮盘赌选择

 for i=1:(N-1)

    r=rand;

    tmp=find(r<=q);

    newbval(i,:)=bval(tmp(1),:);

 end

  newbval(N,:)=bvalxx;%最优保留

  bval=newbval;

%单点交叉

    for i=1:2:(N-1)

       cc=rand;

       if cc<pc

           point=ceil(rand*(2*L-1));%取得一个1到2L-1的整数

           ch=bval(i,:);

           bval(i,point+1:2*L)=bval(i+1,point+1:2*L);

           bval(i+1,point+1:2*L)=ch(1,point+1:2*L);

        end

    end   

    bval(N,:)=bvalxx;%最优保留

    %位点变异

    mm=rand(N,Dim*L)<pm;%N行

    mm(N,:)=zeros(1,Dim*L);%最后一行是精英不变异，强制赋0

    bval(mm)=1-bval(mm); 

end

%输出
figure;

plot(-Bfit1);% 绘制最优适应度进化曲线

bestv   %输出最优适应度值

optxx    %输出最优参数

具体实际例子

目标函数为Rastrigin函数
代码

function y = Rastrigin(x)
% Rastrigin函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
% 编制人：
% 编制日期：
[row,col] = size(x);
if  row > 1 
    error( ' 输入的参数错误 ' );
end
y =sum(x.^2-10*cos(2*pi*x)+10);
%y =-y;

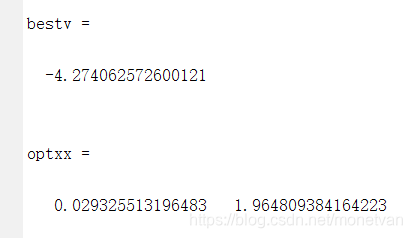
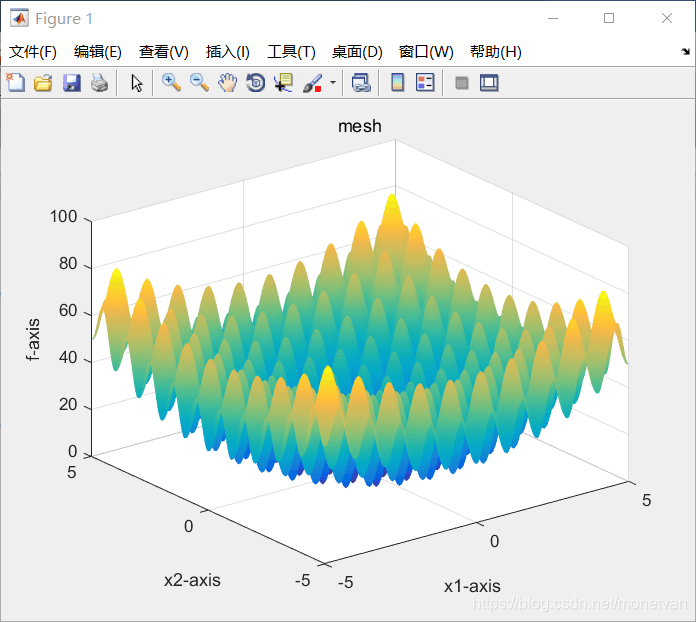
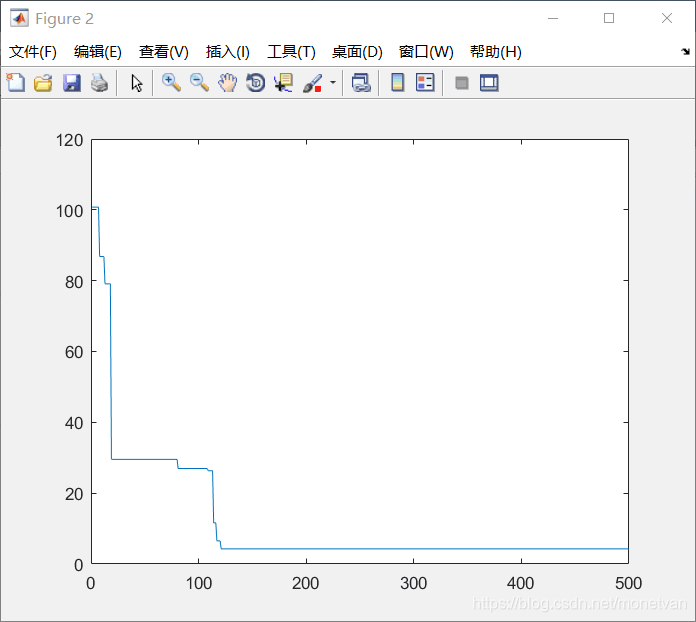
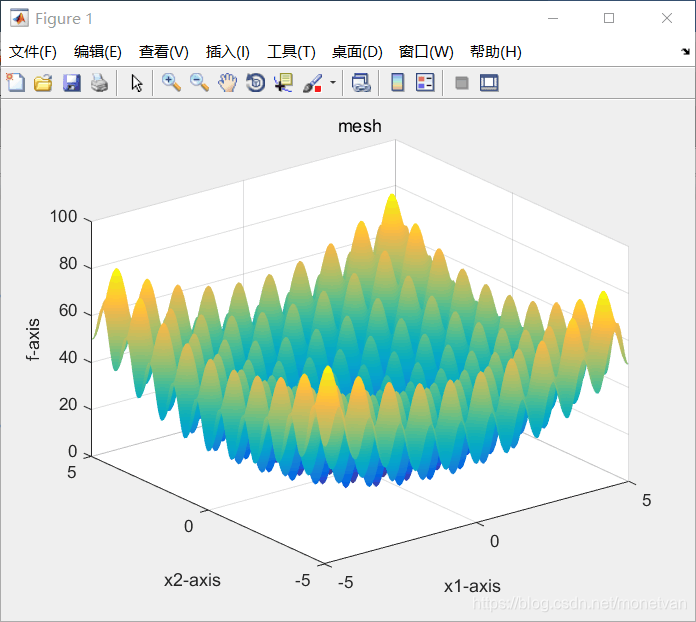
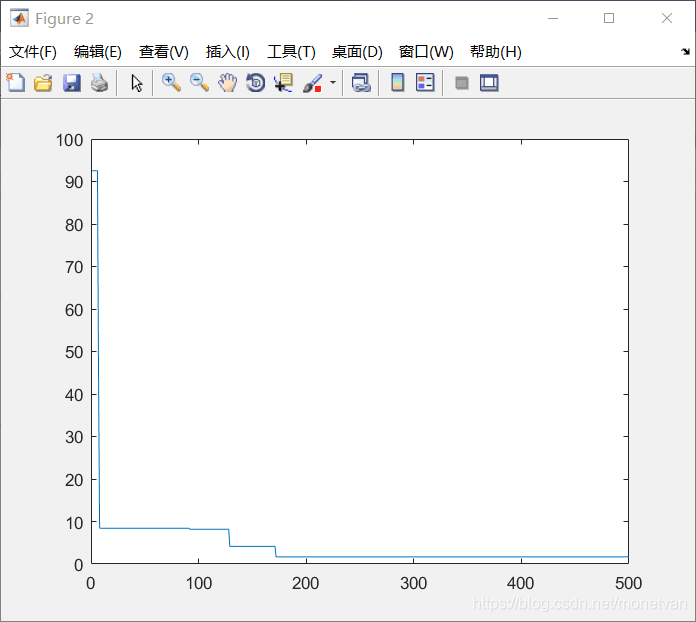
种群数量N=20,目标函数的解空间维度为2的运行结果
图中曲线为最优适应度进化曲线

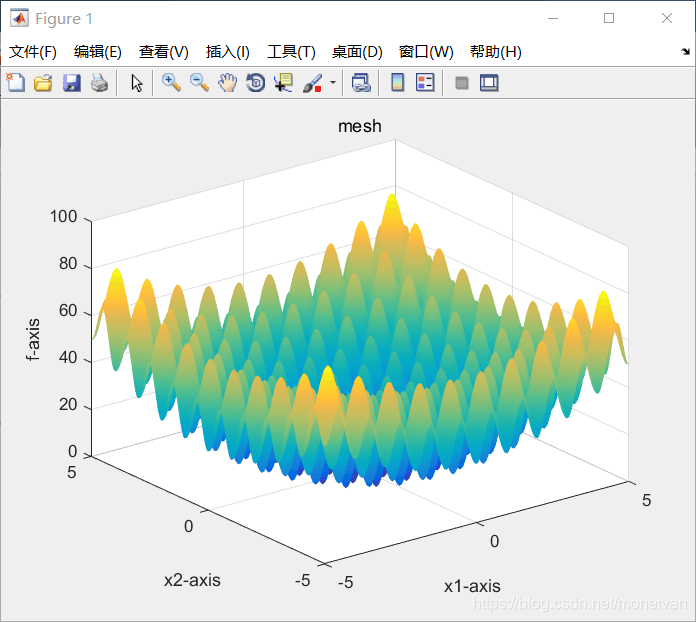
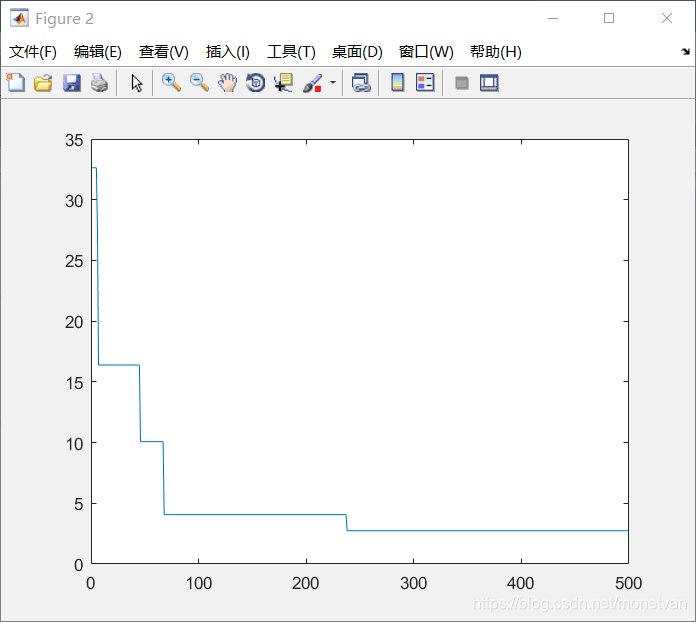
种群数量N=40，目标函数的解空间维度为2的运行结果

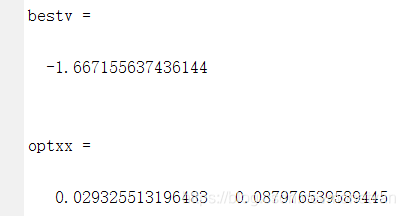
种群数量N=80，目标函数的解空间维度为2的运行结果

种群数量N=20，目标函数的解空间维度为5的运行结果

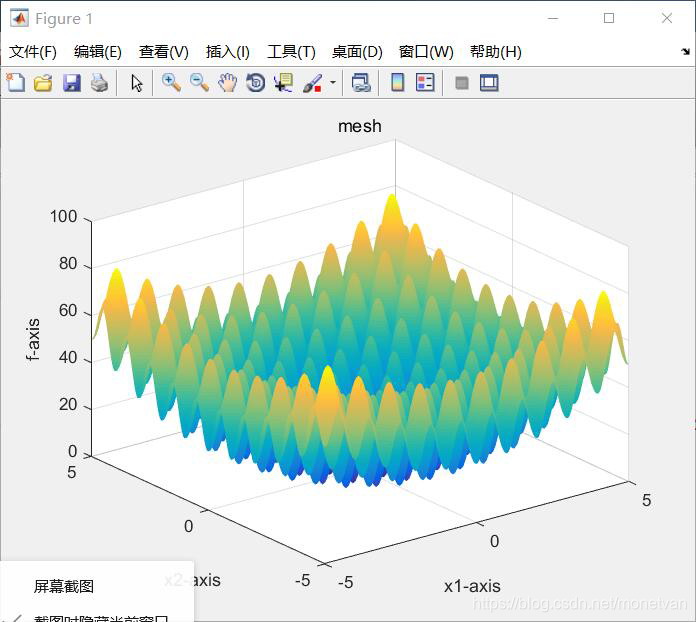
种群数量N=40，目标函数的解空间维度为5的运行结果



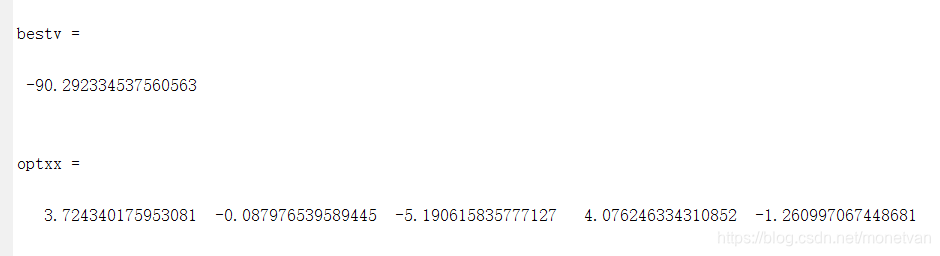
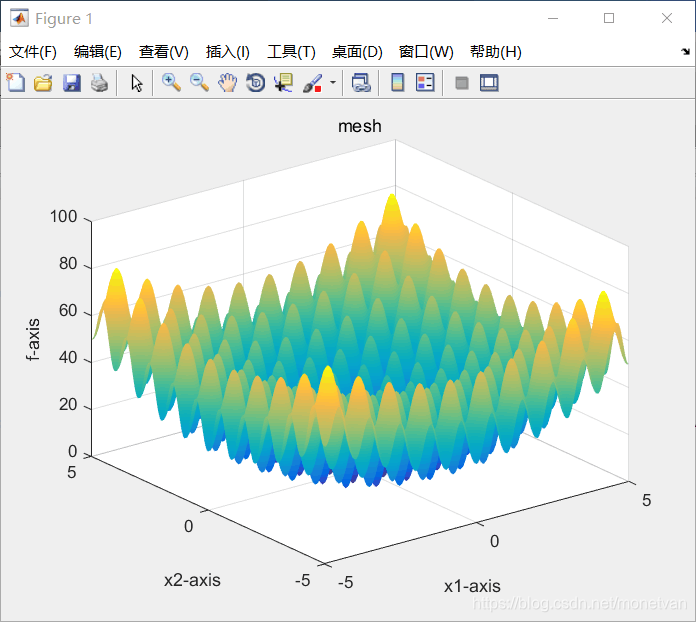
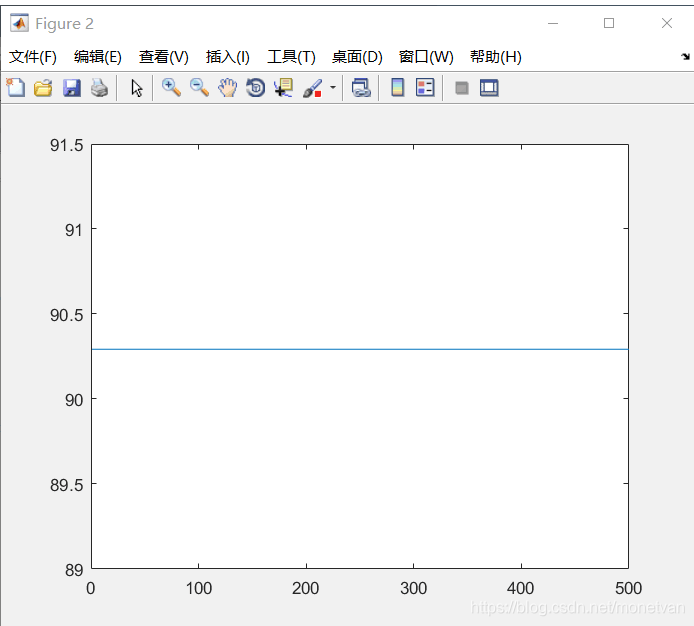
种群数量N=80，目标函数的解空间维度为5的运行结果

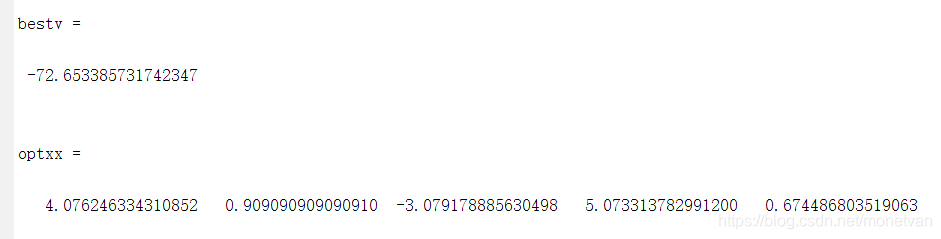
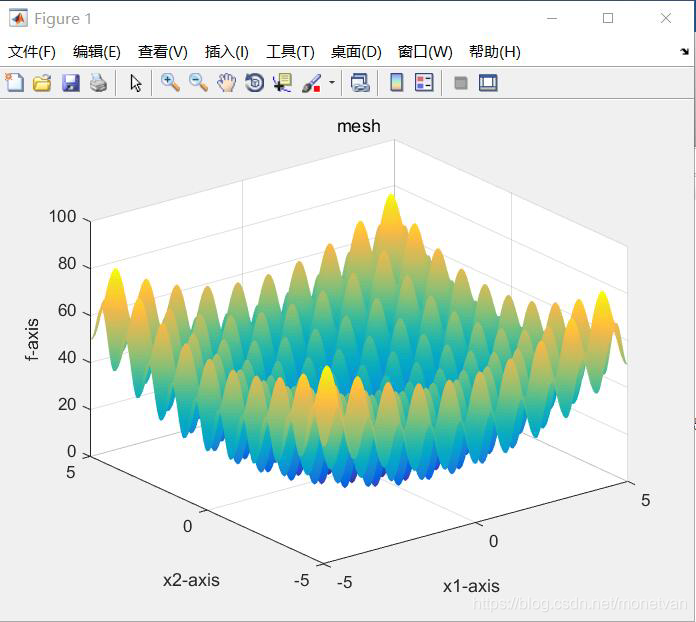
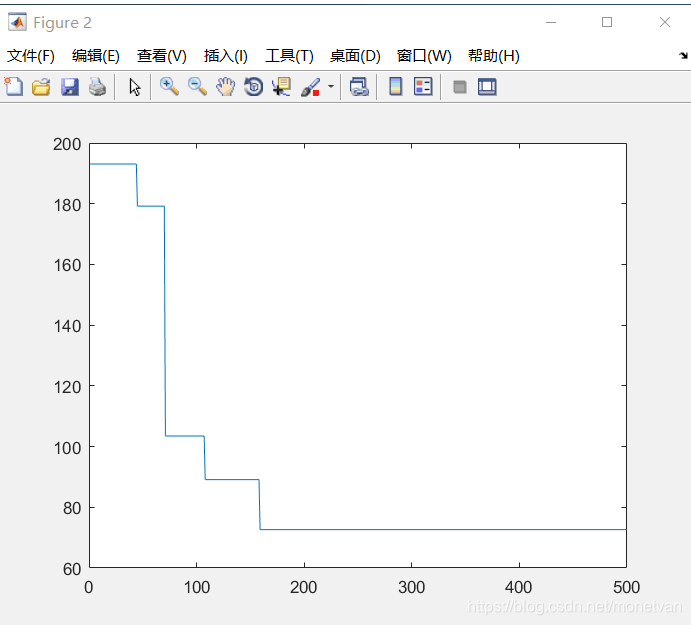
种群数量N=20，目标函数的解空间维度为20的运行结果



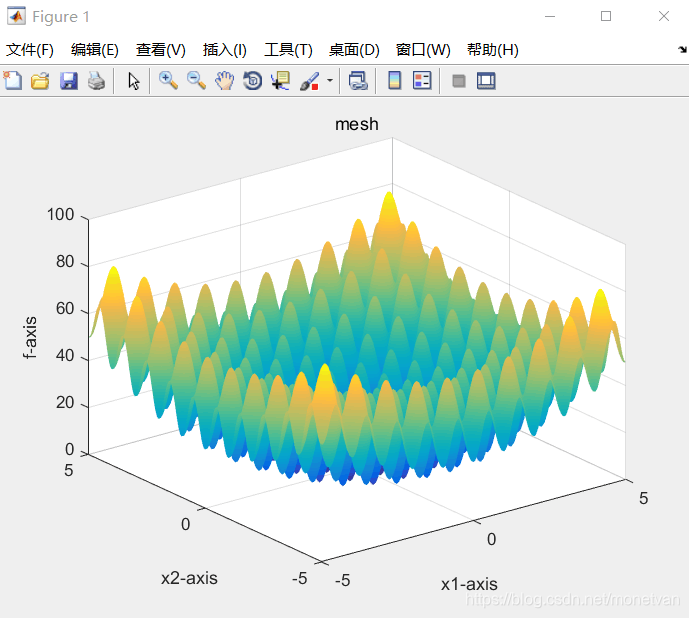
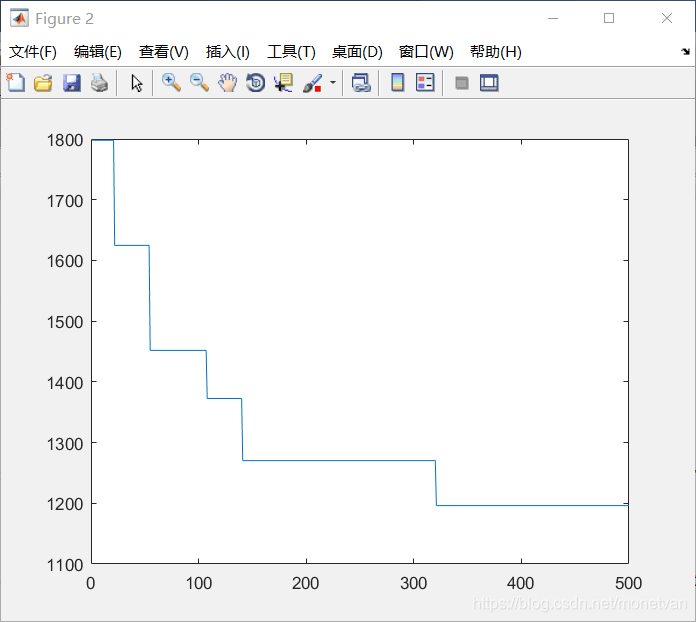
种群数量N=40，目标函数的解空间维度为20的运行结果

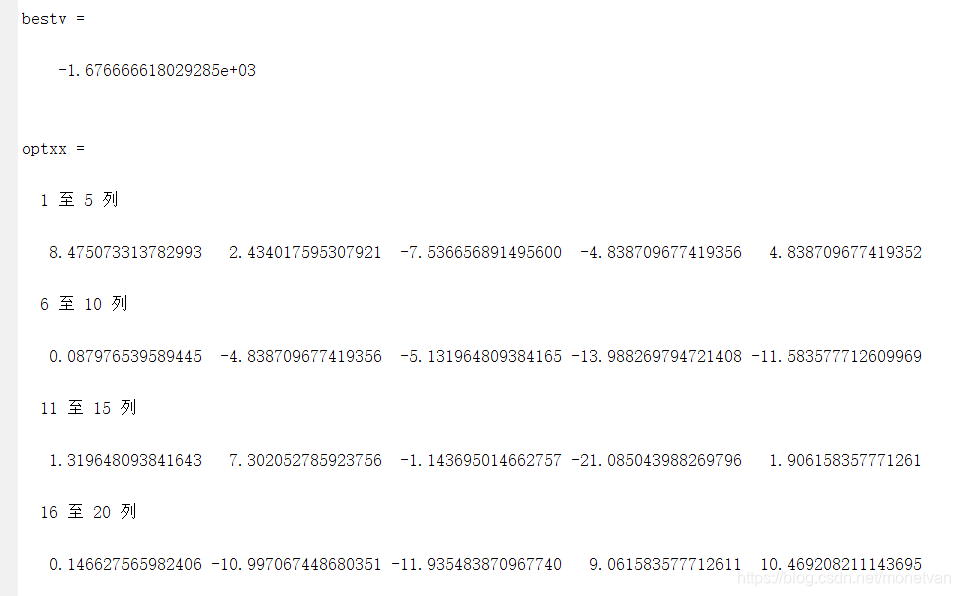
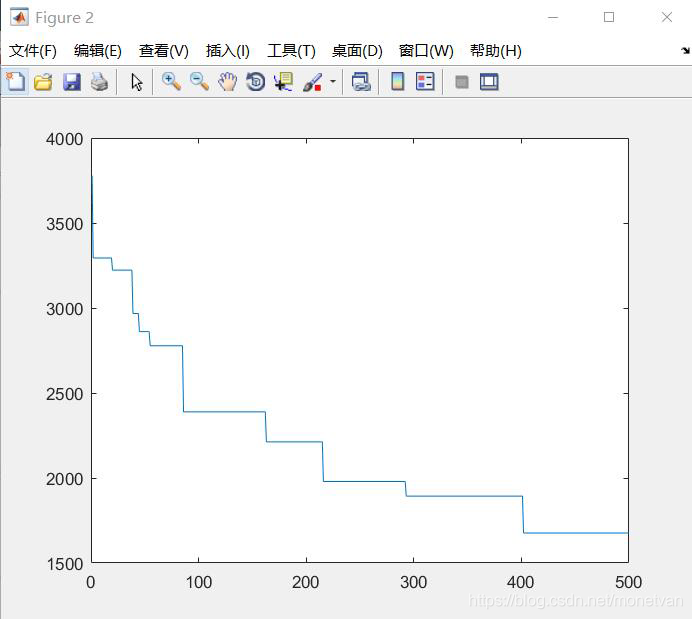
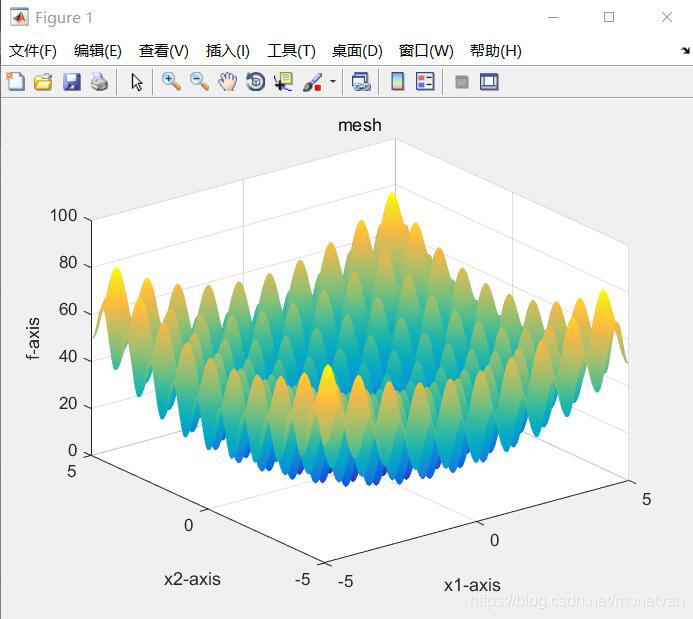
种群数量N=80，目标函数的解空间维度为20的运行结果



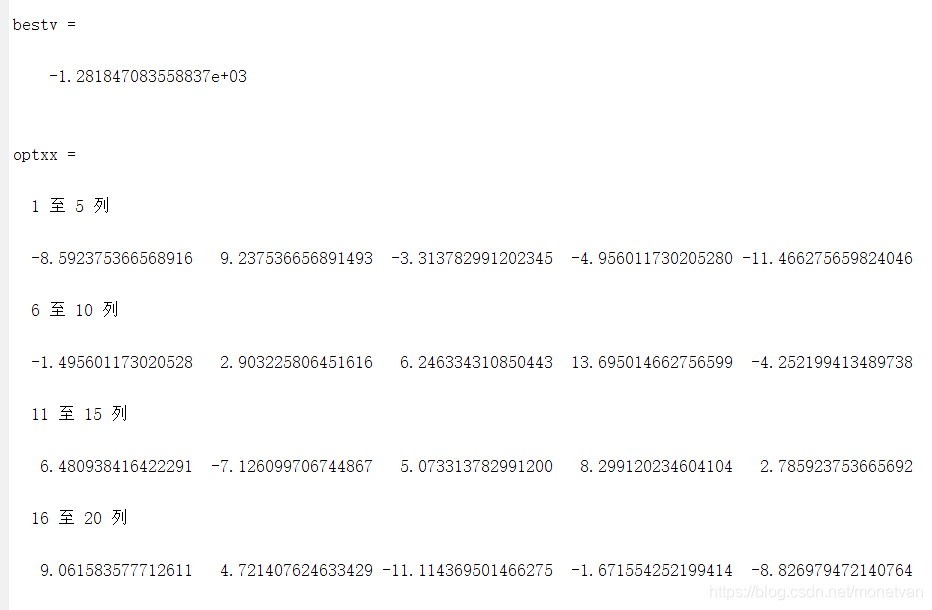
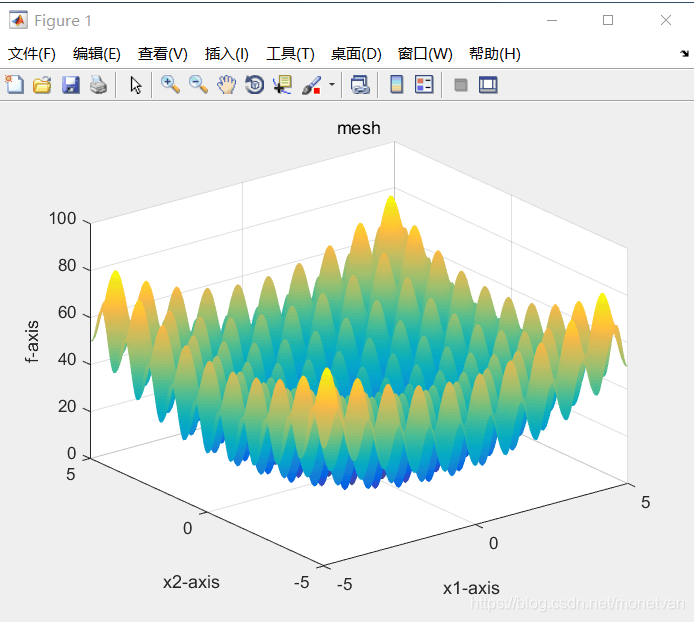
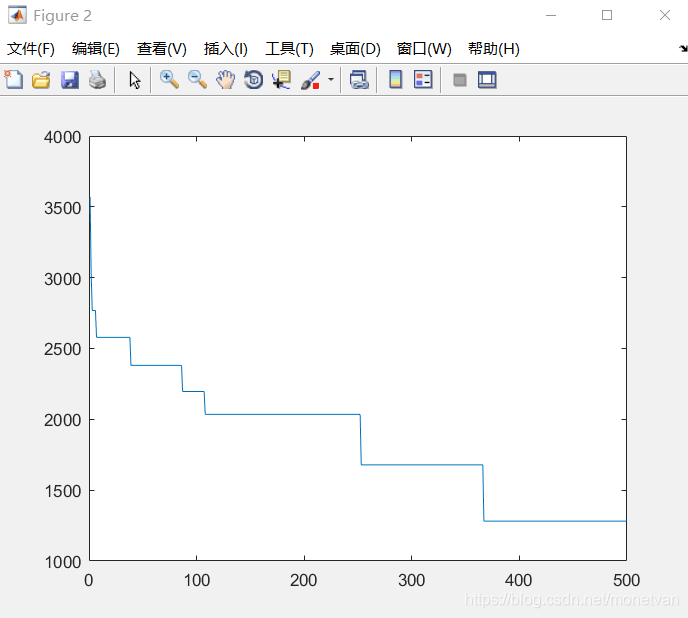
目标函数为Schaffer函数

function y=Schaffer(x)

[row,col]=size(x);
if row>1
    error('输入的参数错误');
end
y1=x(1,1);
y2=x(1,2);
temp=y1^2+y2^2;
y=0.5-(sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
y=-y;

种群数量N=20，目标函数的解空间维度为2的运行结果

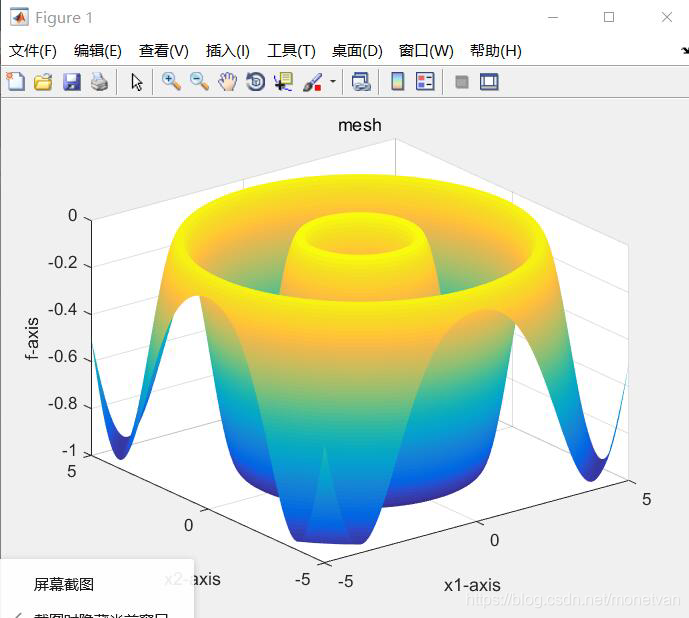
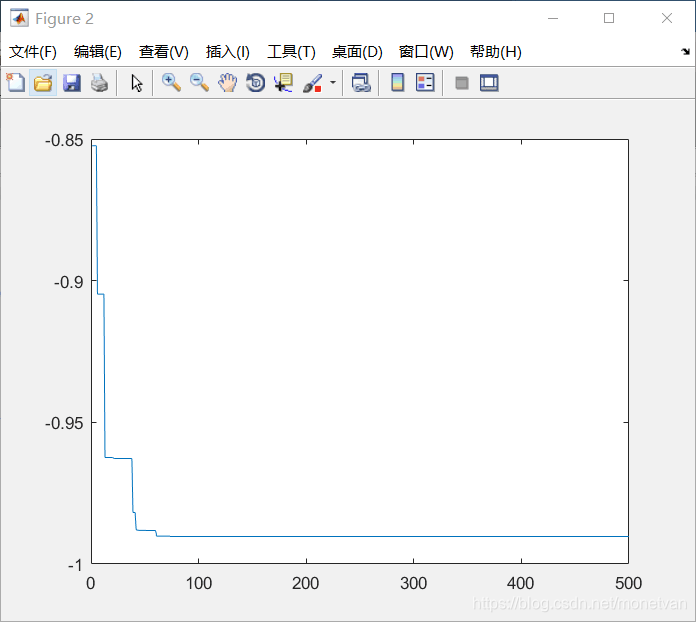
种群数量N=40，目标函数的解空间维度为2的运行结果

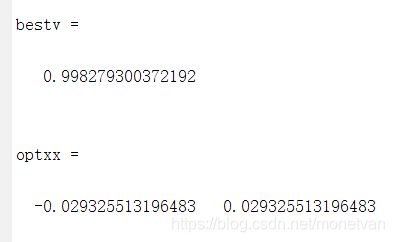
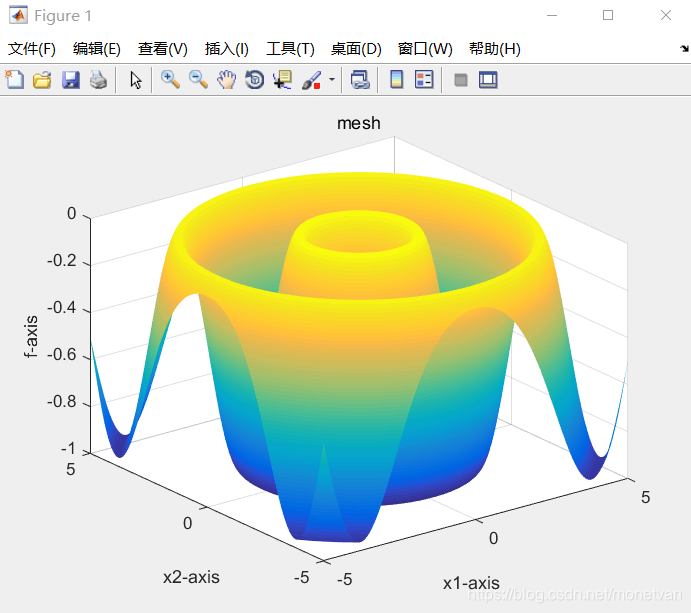
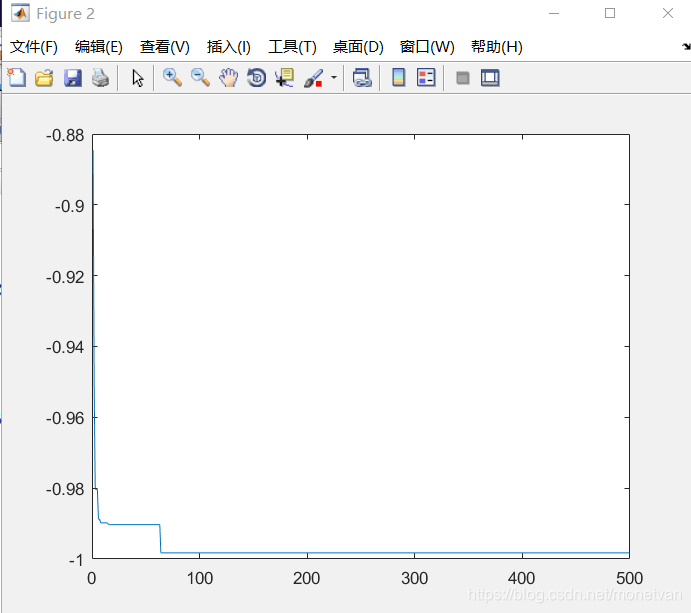
种群数量N=80，目标函数的解空间维度为2的运行结果

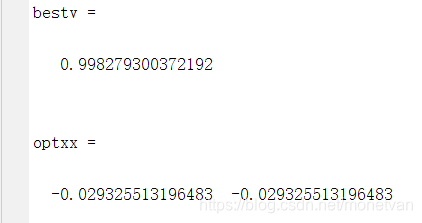
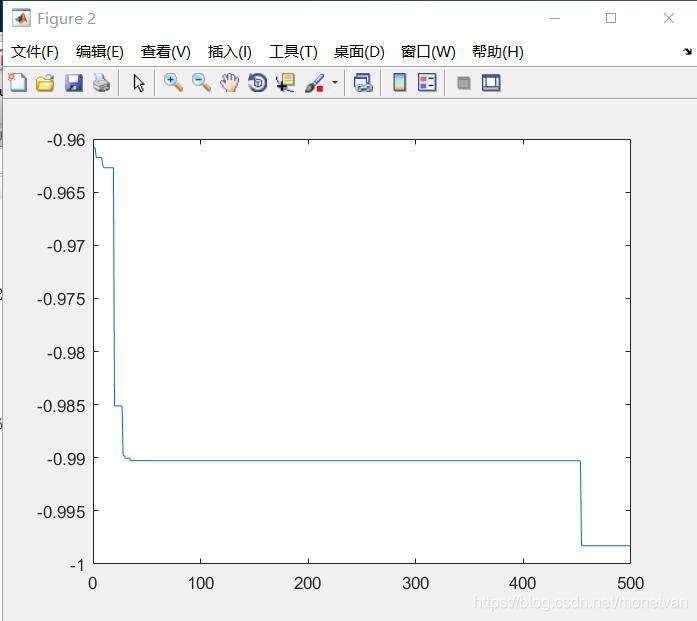
种群数量N=20，目标函数的解空间维度为5的运行结果

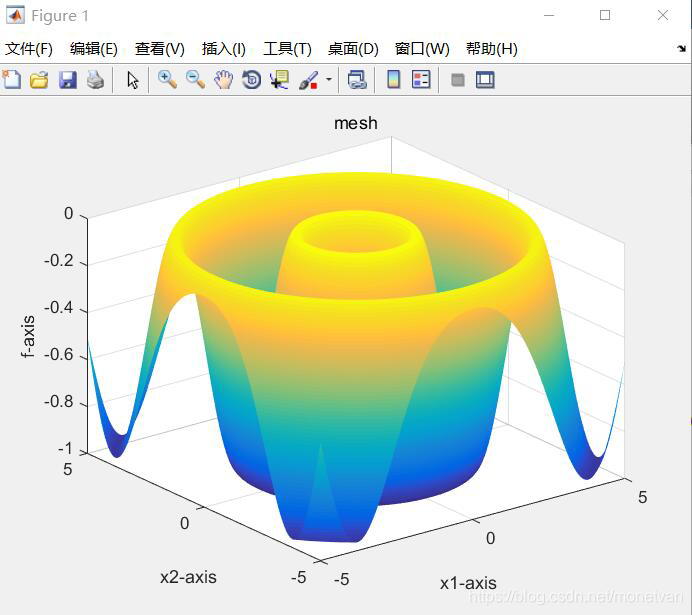
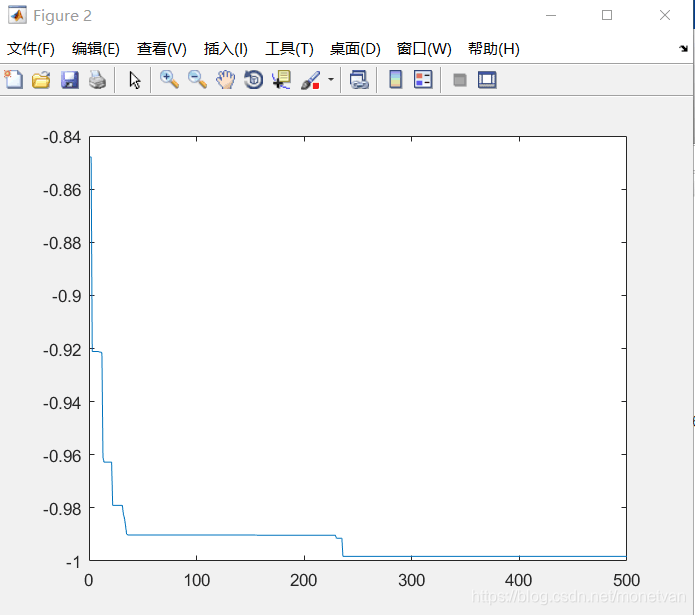
种群数量N=40，目标函数的解空间维度为5的运行结果

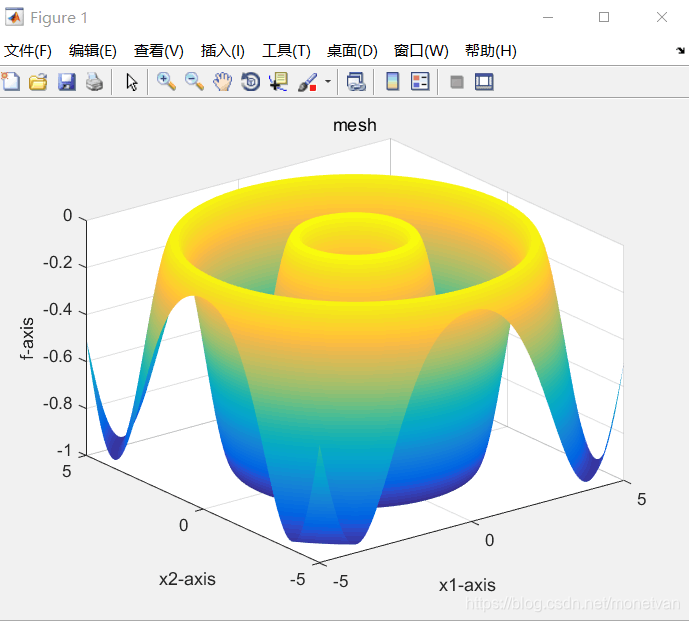
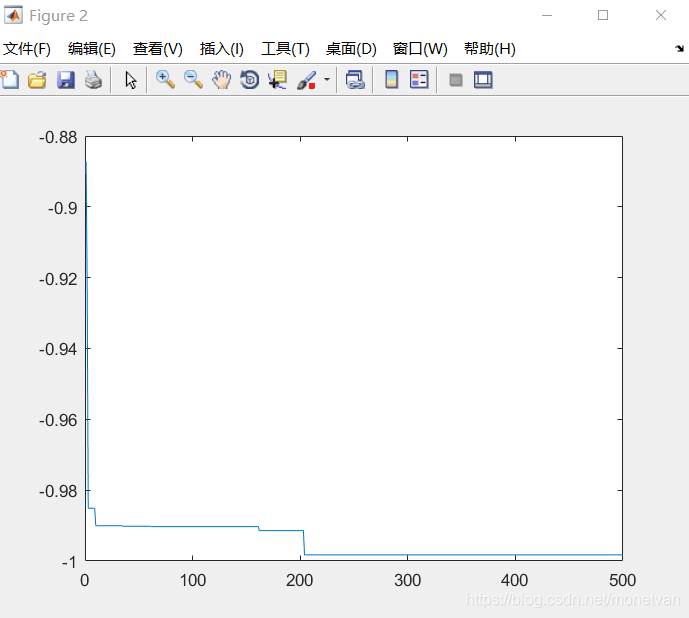
目标函数为Griewank函数

function y=Griewank(x)
%Griewan函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极小点0.
%编制人：
%编制日期：
[row,col]=size(x);
if row>1
    error('输入的参数错误');
end
y1=1/4000*sum(x.^2);
y2=1;
for h=1:col
    y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
%y=-y;

种群数量N=20，目标函数的解空间维度为2的运行结果

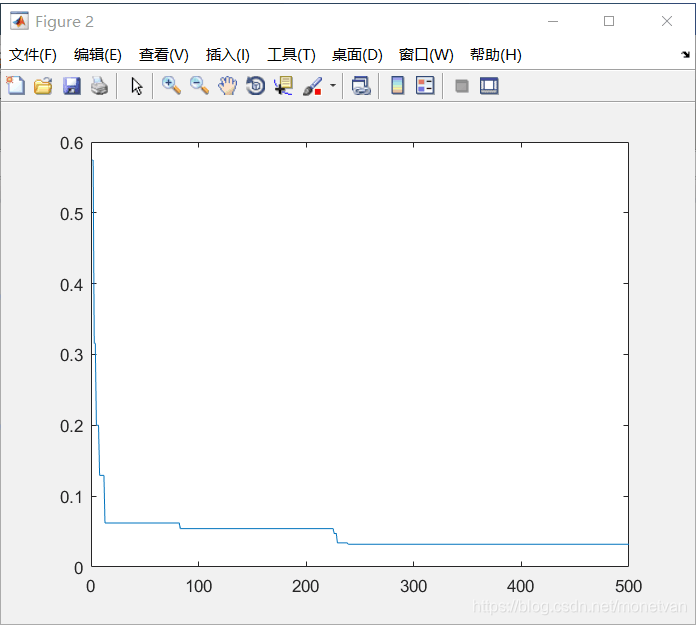
种群数量N=40，目标函数的解空间维度为2的运行结果

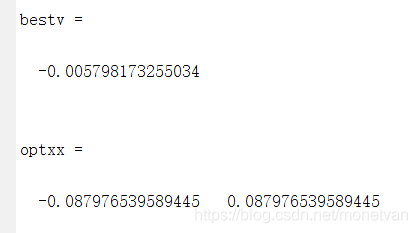
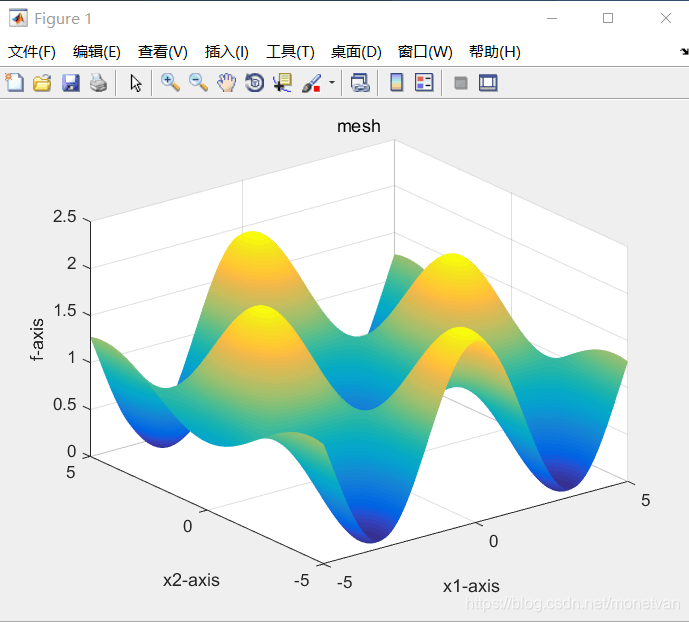
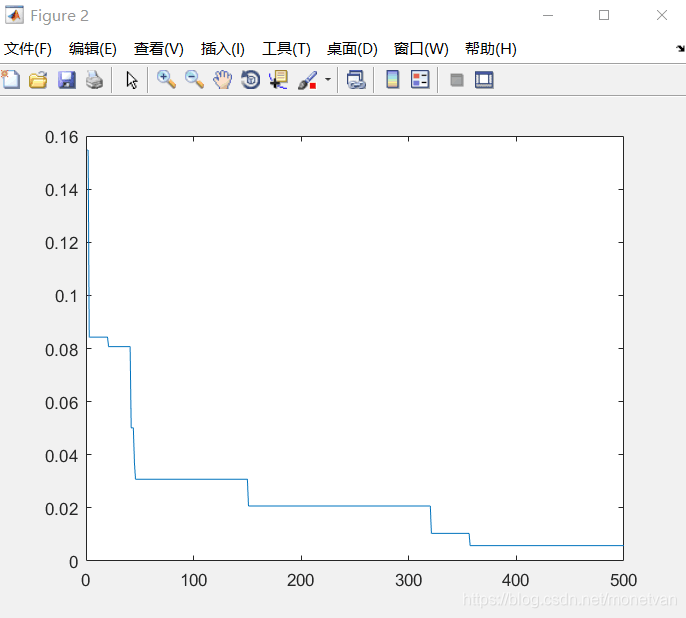
种群数量N=80，目标函数的解空间维度为2的运行结果

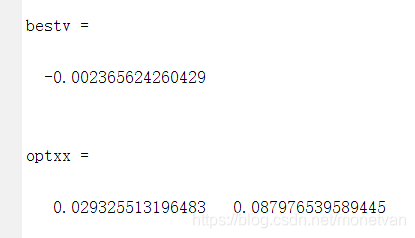
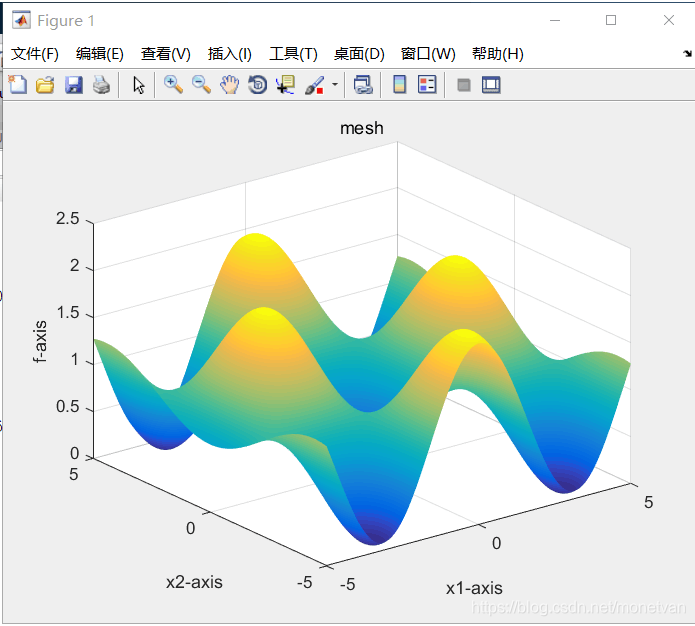
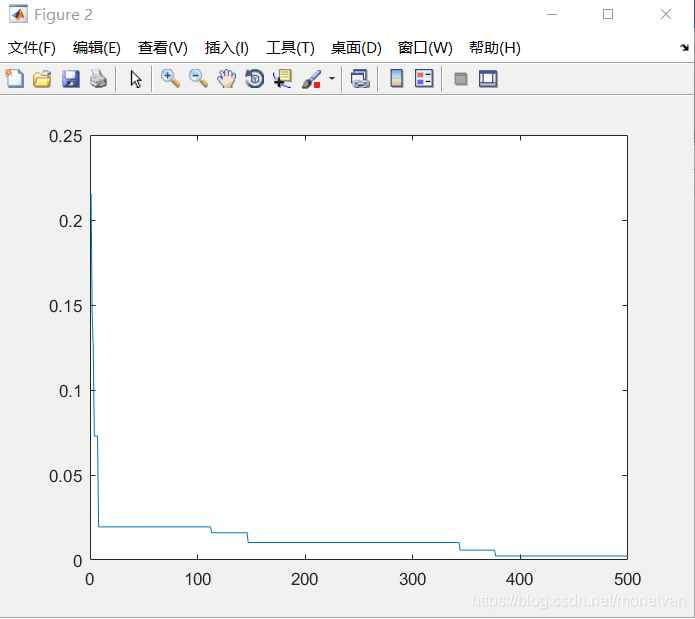
种群数量N=20，目标函数的解空间维度为5的运行结果

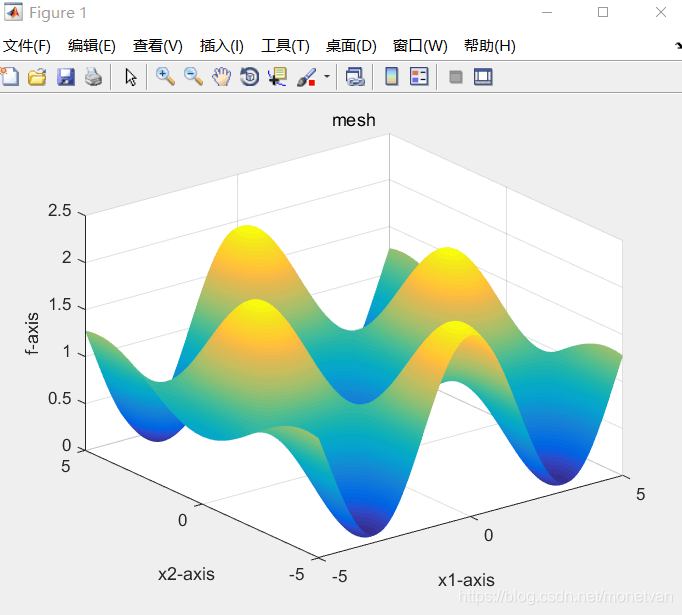
种群数量N=20，目标函数的解空间维度为20的运行结果

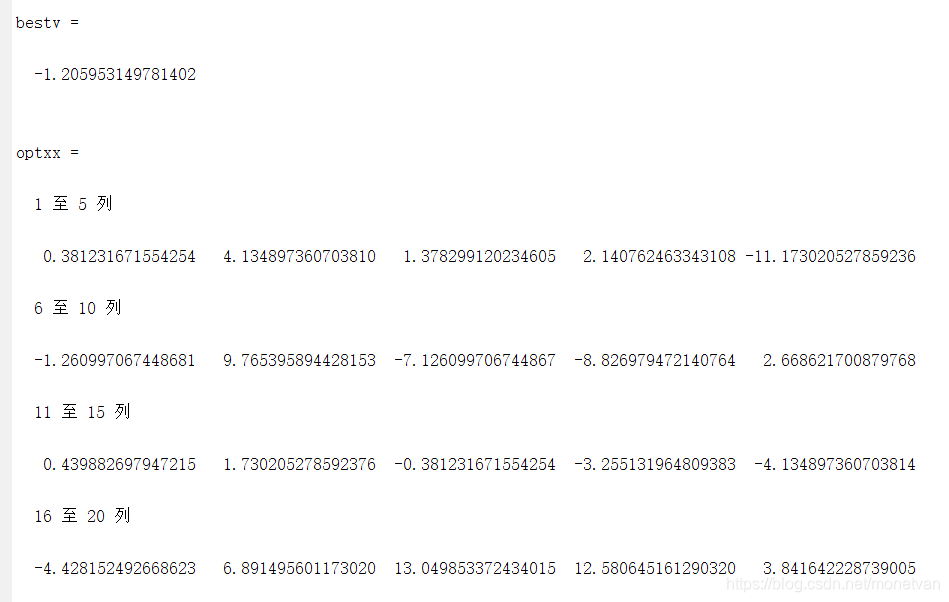
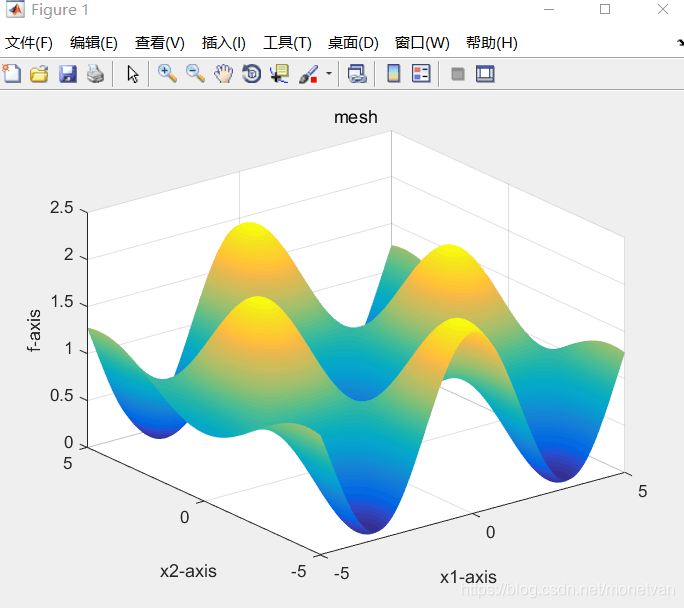
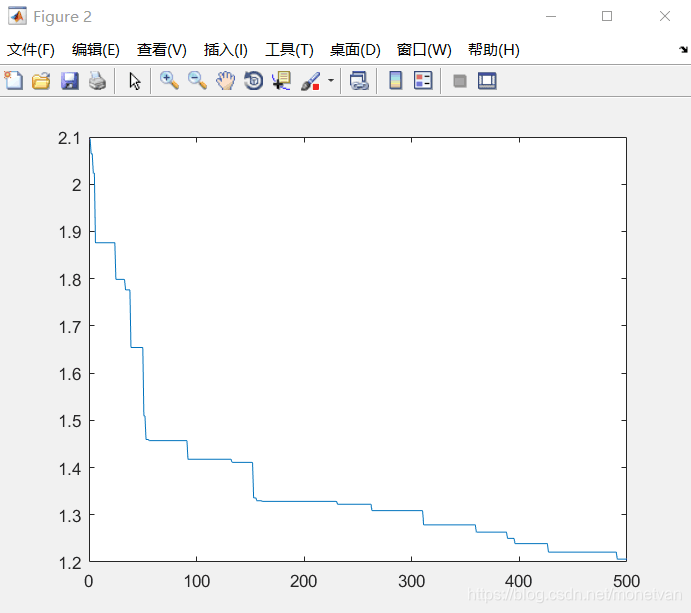
五、对比分析

以上实例从不同空间维度和不同种族数量N两个方面的数据改变具体分析了GA函数的运行速度和最优解精确度。分别取空间维度为2、5、20，以及种族数量为20、40、80。得到如下结论：
（1）在解空间维度相同的条件下，种群数量N越大，需要迭代的次数越多，则GA算法的运行时间越长，最优适应度曲线也在不断变化。
（2）在种群数量N相同的条件下，解空间维度越大，GA算法的运行时间越长。
（3）种群的数量比维数对时间的影响更大。因为维度只用于求解适应值，而在后面的选择、交叉、变异操作中，都需要遍历种群。
（4）适应度函数的选取直接影响遗传算法的收敛速度以及能否找到最优解。一般而言，适应度函数是由目标函数变换而成的。适应度函数设计不当有可能出现个体差异太小导致陷入局部极值的问题。