【深度学习】#13 预训练语言模型

主要参考学习资料：

《动手学深度学习》阿斯顿·张 等 著

【动手学深度学习 PyTorch版】哔哩哔哩@跟李沐学AI

这一篇只发在了公众号上忘记发优快云了……

本章是根据《动手学深度学习》编写的系列最终章。对于原书，该系列省略了第12章计算性能（以计算资源为主）和第15章自然语言处理：应用（以实践为主）。同时本章在原书第14章的基础上，舍去了BERT模型的内容，重点介绍了其一笔带过的GPT模型（考虑到现今GPT的发展势头更好）。当然，对深度学习的探索远不止于此，还有大量的应用场景、模型架构和更深入、更综合、更前沿的知识亟待我们去学习。博主将在补足其他领域知识体系、明确更进一步的学习方向后，继续开拓这一方面的内容。

概述

• 词嵌入是一种能更好体现词元相关性的词向量表示。
• 跳元模型和连续词袋模型通过上下文窗口拟合条件概率训练词向量。
• GloVe通过基于全局统计的共现矩阵训练词向量。
• 生成式预训练Transformer（GPT）是一种基于上下文敏感词表示的通用的任务无关模型。

词嵌入（word2vec）

独热向量

一般的分类模型使用独热向量来表示分类数据，即对于$N$个类别，每个类别对应一个$0\sim N-1$的索引，索引为$i$的类别表示为一个位置$i$的元素为$1$、其余位置元素为$0$的向量。

独热向量易于构建，但对表示词语来说不是一个好的选择，其中一个主要原因是独热向量不能准确表达不同词之间的相似度。例如向量$\mathbf{x},\mathbf{y}\in {\mathbb{R}}^d$的余弦相似度是它们之间夹角的余弦

$$\frac{{\mathbf{x}}^{\top }\mathbf{y}}{||\mathbf{x}||||\mathbf{y}||}\in [-1,1]$$

而任意两个不同词的独热向量之间的余弦相似度为$0$。

word2vec工具是为了解决上述问题而提出的，它将每个词映射到一个固定长度的向量，这些向量能更好地表达不同词之间的相似度和类比关系。

下面将介绍word2vec工具包含的两个模型：跳元模型和连续词袋模型。

跳元模型

在跳元模型中，词元有两个地位，一种是作为模型输入当前词的中心词，一种是模型试图预测的围绕中心词出现的上下文词，被纳入上下文词的半径范围被称为上下文窗口。对于词表中索引为$i$的任何词，跳元模型分别用${\mathbf{v}}_i\in {\mathbb{R}}^d$和${\mathbf{u}}_i\in {\mathbb{R}}^d$表示其用作中心词和上下文词时的两个向量。则在词表$\mathcal{V}$中，给定索引为$c$的中心词$w_c$，生成任何索引为$o$的上下文词$w_o$的条件概率可以通过对向量点积的softmax操作来建模

$$P(w_o\mid w_c)=\frac{\text{exp}({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}{\sum _{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}$$

对于一段长度为$T$的文本序列样本，其中时间步$t$处的词元表示为$w^{(t)}$。假设上下文词是在给定任何中心词的情况下独立生成的，则对于上下文窗口$m$，跳元模型的似然函数是在给定该文本序列的任何词元作为中心词的情况下生成所有上下文词的概率

$$\prod _{t=1}^T\prod _{-m\le j\le m,j\ne 0}P(w^{(t+j)}\mid w^{(t)})$$

其中可以省略$t+j$小于$1$或大于$T$的概率。

训练

跳元模型的参数是词表中每个词的中心词向量和上下文词向量。在训练中，我们通过最大化似然函数学习模型参数，这相当于最小化以下损失函数（对似然函数取负对数）

$$

• \sum_{t=1}^{T} \sum_{-m \leq j \leq m,\ j \neq 0} \text{log}, P(w^{(t+j)} \mid w^{(t)})
  $$

当使用随机梯度下降来最小化损失时，在每次迭代中可以随机抽样一个较短的子序列来计算该子序列的随机梯度。我们考虑涉及中心词$w_c$和上下文词$w_o$的对数条件概率

$$\log P(w_o\mid w_c)={\mathbf{u}}_o^{\top }{\mathbf{v}}_c-\log \left(\sum _{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)\right)$$

则该对数条件概率对于中心词向量${\mathbf{v}}_c$的梯度可通过求相应的微分得到

$$\begin{array}{rl}\frac{\partial \text{log}P(w_o\mid w_c)}{\partial {\mathbf{v}}_c}& ={\mathbf{u}}_o-\frac{\sum _{j\in \mathcal{V}}\exp ({\mathbf{u}}_j^{\top }{\mathbf{v}}_c){\mathbf{u}}_j}{\sum _{i\in \mathcal{V}}\exp ({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\\ & ={\mathbf{u}}_o-\sum _{j\in \mathcal{V}}\left(\frac{\text{exp}({\mathbf{u}}_j^{\top }{\mathbf{v}}_c)}{\sum _{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\right){\mathbf{u}}_j\\ & ={\mathbf{u}}_o-\sum _{j\in \mathcal{V}}P(w_j\mid w_c){\mathbf{u}}_j\end{array}$$

将所有涉及$w_c$的条件概率对于${\mathbf{v}}_c$的梯度累加的结果即为${\mathbf{v}}_c$的最终梯度。其余词向量的梯度也通过类似的微分和累加操作获得。

最终，我们使用跳元模型的中心词向量作为词元表示。

连续词袋模型

和跳元模型相反，连续词袋模型以上下文词作为模型输入，对中心词作出预测。对于词表中索引为$i$的任何词，连续词袋模型分别用${\mathbf{v}}_i\in {\mathbb{R}}^d$和${\mathbf{u}}_i\in {\mathbb{R}}^d$表示其用作上下文词和中心词时的两个向量。

在连续词袋模型的条件概率中，一个中心词$w_c$将由多个上下文词$w_{o_1},\cdots ,w_{o_{2m}}$共同决定（上下文窗口为$m$），因此在softmax操作中，我们对上下文词向量进行平均。设 W o = { w o 1 , ⋯   , w o 2 m } W_o=\{w_{o_1},\cdots,w_{o_{2m}}\} Wo​={wo1​​,⋯,wo2m​​}，${\bar{\mathbf{v}}}_o=({\mathbf{v}}_{o_1},\cdots ,{\mathbf{v}}_{o_{2m}})/(2m)$，则给定上下文词生成任意中心词的条件概率为

$$P(w_c\mid {\mathcal{W}}_o)=\frac{\exp \left({\mathbf{u}}_c^{\top }{\bar{\mathbf{v}}}_o\right)}{\sum _{i\in \mathcal{V}}\exp \left({\mathbf{u}}_i^{\top }{\bar{\mathbf{v}}}_o\right)}$$

给定长度为$T$的文本序列，其中时间步$t$处的词表示为$w^{(t)}$，对于上下文窗口$m$，连续词袋模型的似然函数是在给定其上下文词的情况下生成所有中心词的概率

$$\prod _{t=1}^{T}P(w^{(t)}\mid w^{(t-m)},\dots ,w^{(t-1)},w^{(t+1)},\dots ,w^{(t+m)})$$

训练

连续词袋模型的训练与跳元模型类似，其极大似然估计等价于最小化以下损失函数

$$-\sum _{t=1}^T\text{log}P(w^{(t)}\mid w^{(t-m)},\dots ,w^{(t-1)},w^{(t+1)},\dots ,w^{(t+m)})$$

其中求和的每一项为

$$\log P(w_c\mid {\mathcal{W}}_o)={\mathbf{u}}_c^{\top }{\bar{\mathbf{v}}}_o-\log \left(\sum _{i\in \mathcal{V}}\exp \left({\mathbf{u}}_i^{\top }{\bar{\mathbf{v}}}_o\right)\right)$$

该对数条件概率对于任意上下文词向量${\mathbf{v}}_{o_i}(i=1,\cdots ,2m)$的梯度可通过求相应的微分得到

$$\begin{array}{rl}\frac{\partial \log P(w_c\mid {\mathcal{W}}_o)}{\partial {\mathbf{v}}_{o_i}}& =\frac{1}{2m}\left({\mathbf{u}}_c-\sum _{j\in \mathcal{V}}\frac{\exp ({\mathbf{u}}_j^{\top }{\bar{\mathbf{v}}}_o){\mathbf{u}}_j}{\sum _{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\bar{\mathbf{v}}}_o)}\right)\\ & =\frac{1}{2m}\left({\mathbf{u}}_c-\sum _{j\in \mathcal{V}}P(w_j\mid {\mathcal{W}}_o){\mathbf{u}}_j\right)\end{array}$$

将所有涉及$w_{o_i}$的条件概率对于${\mathbf{v}}_{o_i}$的梯度累加的结果即为${\mathbf{v}}_{o_i}$的最终梯度。其余词向量的梯度也通过类似的微分和累加操作获得。

最终，我们使用连续词袋模型的上下文词向量作为词元表示。

训练后的跳元模型和连续词袋模型使用各自作为输入的词向量作为词元表示，这是实验证明的结果。尽管二者采用不同的方式，但它们本质上都是学习词元之间的相似性，可以广泛应用于相同的自然语言处理任务，而一些具体的差异如下表所示

特性	跳元模型	连续词袋模型
数据需求	适合大型数据集和罕见词	适合小型数据集和高频词
语义捕捉能力	对常见词更稳定	对复杂语义更敏感
典型应用场景	通用语料、快速训练	专业领域、低频词、细粒度语义分析

近似训练

原始的word2vec模型在梯度计算中包含项数与词表大小一样的求和，这在一个通常有上万个词的词表上的计算成本是巨大的。为了降低计算复杂度，我们需要一些近似训练的方法。由于跳元模型和连续词袋模型的相似性，我们以跳元模型为例讨论。

负采样

对于给定文本序列中的一处中心词，假设上下文窗口为$m$，则其真实出现的上下文词种类至多只有$2m-1$个，词表中几乎大部分词是不存在的，因此计算资源被大量消耗在了和非真实上下文词相关的计算上。我们仍需考虑所有真实的上下文词，但对于那些非真实上下文词，可以通过只采样一部分来近似。

对于真实的上下文词，我们称之为正样本，而非真实上下文词则为负样本，通过采样一部分负样本来近似条件概率的方法称为负采样。在负采样中，任意上下文词$w_o$作为中心词$w_c$的正样本的事件概率表示如下

$$P(D=1|w_c,w_o)=\sigma ({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)$$

其中$\sigma$使用了sigmoid激活函数的定义

$$\sigma (x)=\frac{1}{1+\exp (-x)}$$

则当上下文词向量和中心词向量的点积越大，正样本事件概率越大。相应地，任意上下文词$w_o$作为中心词$w_c$的负样本是其作为正样本的对立事件

$$P(D=0|w_c,w_o)=1-\sigma ({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)$$

负采样假设所有上下文词作为正样本和负样本出现的事件都是相互独立的，则对于给定中心词$w_c$时上下文词$w_o$出现的条件概率，我们可以用$w_o$作为正样本，同时$w_o$之外的$K$个采样作为负样本的联合概率分布来近似

$$P(w^{(t+j)}\mid w^{(t)})=P(D=1\mid w^{(t)},w^{(t+j)})\prod _{k=1,w_k\sim P(w)}^{K}P(D=0\mid w^{(t)},w_k)$$

其中采样的$K$个词语称为噪声词，$P(w)$是预定义的采样概率分布。以该近似作为需要最大化的似然函数相当于最小化如下负对数损失

$$\begin{array}{rl}-\log P(w^{(t+j)}\mid w^{(t)})=& -\log P(D=1\mid w^{(t)},w^{(t+j)})-\sum _{k=1,w_k\sim P(w)}^K\log P(D=0\mid w^{(t)},w_k)\\ =& -\log \sigma \left({\mathbf{u}}_{i_{t+j}}^{\top }{\mathbf{v}}_{i_t}\right)-\sum _{k=1,w_k\sim P(w)}^K\log \left(1-\sigma \left({\mathbf{u}}_{h_k}^{\top }{\mathbf{v}}_{i_t}\right)\right)\\ =& -\log \sigma \left({\mathbf{u}}_{i_{t+j}}^{\top }{\mathbf{v}}_{i_t}\right)-\sum _{k=1,w_k\sim P(w)}^K\log \sigma \left(-{\mathbf{u}}_{h_k}^{\top }{\mathbf{v}}_{i_t}\right).\end{array}$$

现在，每个训练步的梯度计算成本与词表大小无关，而是线性依赖$K$。超参数$K$越小，单步梯度计算成本越小。

层序softmax

层序softmax通过构建二叉树组织所有类别，将扁平化的大规模分类问题转化为多层次的二分类问题。

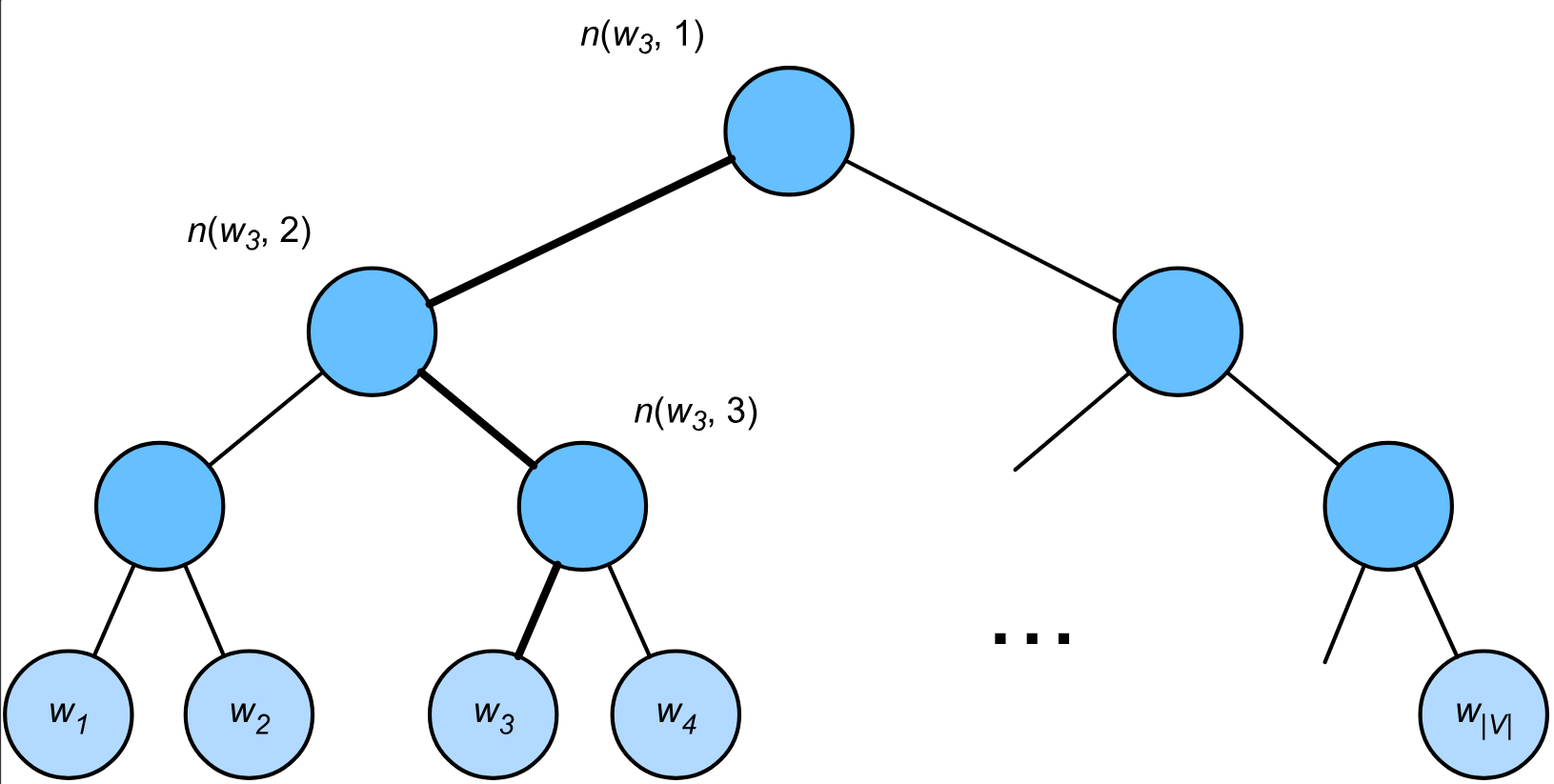
对于给定中心词$w_c$，上下文词$w_o$（图中为$w_3$）出现的条件概率通过由根节点到$w_3$叶子节点路径上的一系列二分类决策近似。用$n(w,j)$表示词$w$对应路径上的第$j$个节点，其上下文词向量为${\mathbf{u}}_{n(w,j)}$，则在每个节点，上下文词隶属于左子节点的概率为$\sigma ({\mathbf{u}}_{n(w,j)}^{\top }{\mathbf{v}}_c)$，隶属于右子节点的概率为$-\sigma ({\mathbf{u}}_{n(w,j)}^{\top }{\mathbf{v}}_c)$（二者概率之和为$1$）。最终条件概率被近似为$w_o$所在路径上所有二分类决策的联合概率分布

$$P(w_o\mid w_c)=\prod _{j=1}^{L(w_o)-1}\sigma \left([[n(w_o,j+1)=\text{leftChild}(n(w_o,j))]]\cdot {\mathbf{u}}_{n(w_o,j)}^{\top }{\mathbf{v}}_c\right)$$

其中$[[n(w_o,j+1)=\text{leftChild}(n(w_o,j))]]$在$n(w_o,j+1)$是$n(w_o,j)$的左子节点时为$1$，反之为$0$。$L(w_o)$表示词$w_o$从根节点到叶子节点路径上的节点数。以图中给定中心词$w_c$生成$w_3$的条件概率为例，我们通过对加粗路径遍历得出

$$P(w_3\mid w_c)=\sigma ({\mathbf{u}}_{n(w_3,1)}^{\top }{\mathbf{v}}_c)\cdot \sigma (-{\mathbf{u}}_{n(w_3,2)}^{\top }{\mathbf{v}}_c)\cdot \sigma ({\mathbf{u}}_{n(w_3,3)}^{\top }{\mathbf{v}}_c)$$

由于二叉树中所有叶子节点的概率之和为$1$，路径概率的乘积自然被归一化，因此不需要像普通softmax显式考虑其他上下文词。对于大小为$|V|$的词表，二叉树的根节点到叶子节点的最长路径约为${\log }_2|V|$，其计算复杂度也为$O({\log }_2|V|)$。

全局向量的词嵌入（GloVe）

在word2vec中，我们捕捉的是局部的上下文信息，即使用一个上下文窗口在文本序列中滑移，每次滑移会学习到更大的窗口内中心词和上下文词的条件概率。

但是既然已经有了完整的语料库，我们完全可以通过全局统计的方式，直接得到以某个词为中心词，所有词出现在其上下文窗口中的频率，进而得到相应的条件概率。给定语料库的中心词$w_i$，在全局统计下，其生成上下文词$w_j$的条件概率$p_{ij}\dot{=}P(w_j|w_i)$被称为共现概率，而以行为中心词，以列为上下文词，以中心词-上下文词对的共现概率（也常用共现频率）为元素的值的矩阵被称为共现矩阵。

下表给出了一个大型语料库统计数据中，给定中心词ice和steam的部分共现概率及其比值：

${\mathbf{w}}_k$	solid	gas	water	fashion
$p_1=P(w_k\mid ice)$	0.00019	0.000066	0.003	0.000017
$p_2=P(w_k\mid steam)$	0.000022	0.00078	0.0022	0.000018
$p_1/p_2$	8.9	0.085	1.36	0.96

根据表中数据可见，由于较大的基数，许多共现概率的值是很小的，而通过比值我们可以放大不同中心词-上下文词对的分布差异。对于跳元模型来说，对于相同的中心词$w_i$，不同的上下文词$w_j$和$w_k$的相对共现概率可拟合如下

$$\frac{P(w_j|w_i)}{P(w_k|w_i)}=\frac{\exp \left({\mathbf{u}}_j^{\top }{\mathbf{v}}_i\right)}{\exp \left({\mathbf{u}}_k^{\top }{\mathbf{v}}_i\right)}\approx \frac{p_{ij}}{p_{ik}}$$

更直接地，共现概率比$\frac{p_{ij}}{p_{ik}}$就等于共现频率比$\frac{x_{ij}}{x_{ik}}$。在这种关系下，我们可以选择$\exp ({\mathbf{u}}_j^{\top }{\mathbf{v}}_i)\approx x_{ij}$，两边取对数得到${\mathbf{u}}_j^{\top }{\mathbf{v}}_i\approx \log x_{ij}$。而在实际训练过程中，我们还需要使用可学习的偏置项

$${\mathbf{u}}_j^{\top }{\mathbf{v}}_i+b_i+c_j\approx \log x_{ij}$$

其中$b_i$为中心词偏置，$c_j$为上下文词偏置。偏置项可以拟合语料库本身带来的固有频率误差，并处理共现频率$x_{ij}=0$的极端情况，对低频词进行补偿，进一步提高模型的表达能力，使其更加稳定。

最终，GloVe模型通过对上式的加权平方误差得到需要降低的损失函数

$$\sum _{i\in \mathcal{V}}\sum _{j\in \mathcal{V}}h(x_{ij}){\left({\mathbf{u}}_j^{\top }{\mathbf{v}}_i+b_i+c_j-\log x_{ij}\right)}^2$$

$h(x_{ij})$是平方误差项的权重，其计算如下

$$h(x)=\{\begin{array}{llc}(\frac{x}{x_{\text{max}}}{)}^{\alpha }& ,& x<x_{\text{max}}\\ 1& ,& x⩾x_{\text{max}}\end{array}$$

它的目的是抑制低频词噪声对模型优化的影响，低频词因为统计稀疏，一些偶然因素将导致模型学习到不可靠的语义。对于越低的频率，$(\frac{x}{x_{\text{max}}}{)}^{\alpha }$将为其赋予更低的权重。而当频率超过预定义的最大频率$x_{\max }$时，权重将限制为$1$，避免高频词完全主导优化过程。

生成式预训练Transformer（GPT）

我们目前介绍的词嵌入模型都是上下文无关的，即一个词元在不同上下文语境下只有一种表示。上下文无关的表示具有明显的局限性，例如在“a crane is flying（一只鹤在飞）”和“a crane driver came（一名吊车司机来了）”中，“crane”一词具有完全不同的含义，同一个词可以根据上下文被赋予不同的表示。

这推动了上下文敏感的词表示的发展，即词的表示取决于它们的上下文。在上下文敏感的词表示中，词元$x$的表示是函数$f(x,c(x))$，其取决于$x$及其上下文函数$c(x)$。一种典型的模型是ELMo，它将预训练的双向LSTM的所有中间层表示组合为输出表示，并与现有模型中词元的原始表示（例如GloVe）连接起来。

但是ELMo本身只是一个提供词向量的通用特征提取器，在面对不同的自然语言处理任务时，它还需要搭配定制的下游任务模型。而且其使用的双向LSTM难以在实际应用时被微调，一方面梯度沿时间反向传播和双向协调为其训练带来困难，另一方面串行的序列计算也使得微调无法充分利用GPU并行计算能力，计算速度慢。然而，为每个自然语言处理任务设计一个特定的架构并非易事。生成式预训练Transformer（GPT）则是一种具有上下文敏感表示特性的通用的任务无关模型。

架构

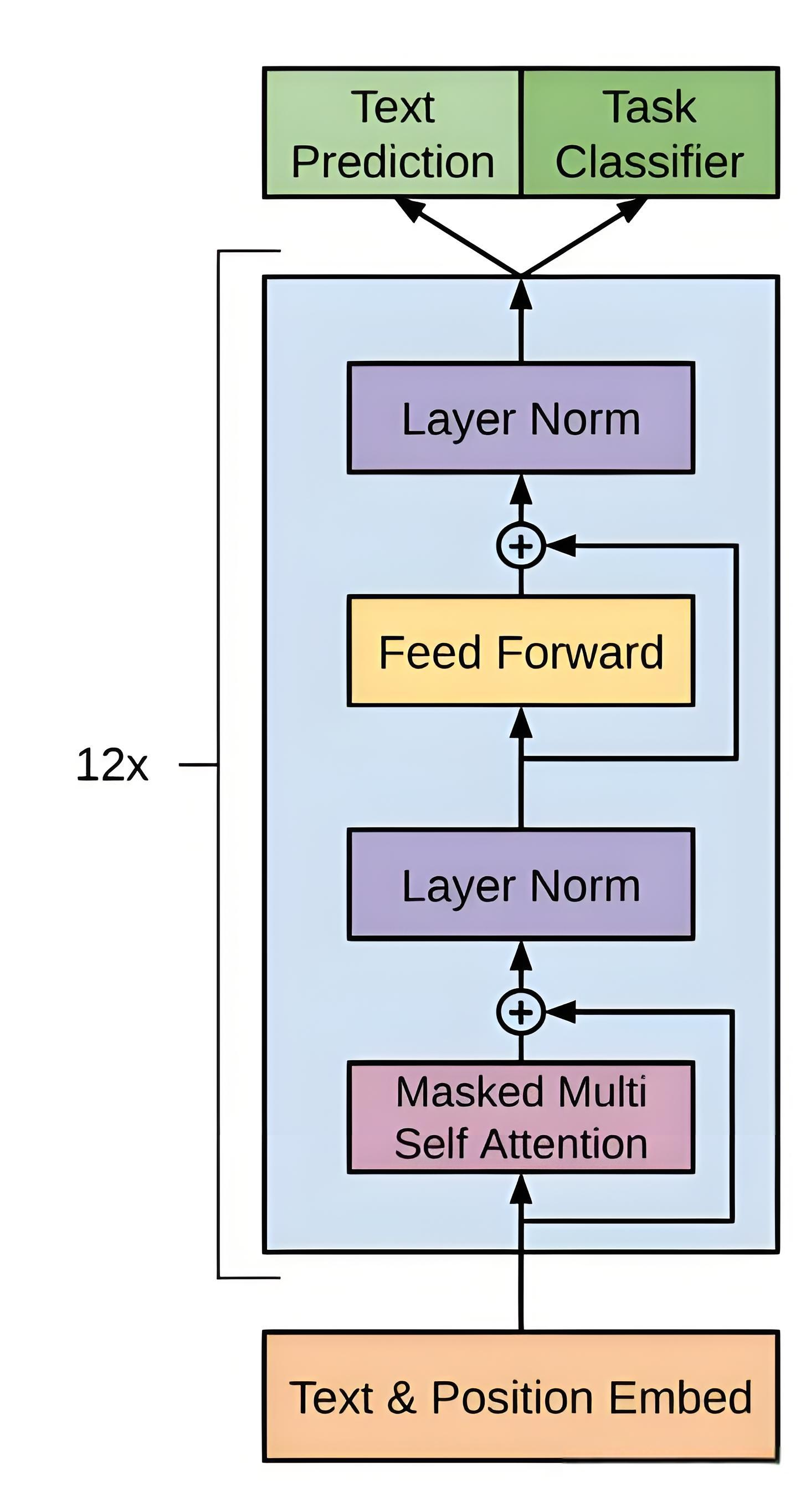
GPT的基本架构包括输入表示层、Transformer解码器层和线性输出层。

输入表示层

输入表示层是GPT将词元转化为向量表示的部分，其主要包括词嵌入和位置编码两个工作。

嵌入矩阵

Transformer的词嵌入通过嵌入矩阵的训练来学习。嵌入矩阵由词表中所有词的词向量组成，这也是嵌入矩阵学习的参数。对于大小为$V$的词表、维度为$d$的词向量，嵌入矩阵$E\in {\mathbb{R}}^{V\times d}$，其通过索引返回一个词元的词向量。和之前介绍的词嵌入模型不同的是，嵌入矩阵不是一个可以独立学习词表示的模型，而是与整个Transformer绑定，通过训练预测任务时的反向传播来更新参数。

嵌入矩阵可以使用预训练的词嵌入模型初始化来加速收敛，但现代大模型更常采用随机初始化来确保参数的协同更新，并预防知识冲突。除此之外，传统的词嵌入模型维度在数百维，而大模型的嵌入维度达到了上万维，拥有更大的表示空间。

子词嵌入

在英语中，同一个词有不同的时态、分词或单复数形式，而许多不同的词之间也可以通过词根词缀联系起来。这种词的形式与构成模式在语言中广泛存在，因此通过对词的内部结构进行拆分，既可以更好地把握单词之间的相关性，也能更好地表示一些罕见词，甚至是词表没有考虑到的词，这就是子词嵌入。

以“where”为例，拆解字词的第一步是在词的开头和末尾添加特殊字符“<”和“>”来标记前缀和后缀。然后从词中提取以$n$个字符为单位的子词，例如$n=3$时，我们将获得长度为$3$的所有子词“<wh”“whe”“her”“ere”“re>”和特殊子词“<where>”。通常我们会使用多个$n$的取值进行拆分。

对于任意词$w$，用$G_w$表示其在所有$n$的取值下拆分的子词与特殊子词的集合，词表中子词$g$的向量为${\mathbf{z}}_g$，则$w$的词向量${\mathbf{v}}_w$是其子词向量的和

$${\mathbf{v}}_w=\sum _{g\in G_w}{\mathbf{z}}_g$$

位置编码

在注意力机制一章中，我们介绍了人工注入的固定位置编码。而在GPT中，位置编码是可学习的，它将位置索引映射为可训练的向量参数，通过数据驱动优化位置表示，能够更灵活地适配任务需求。位置编码的学习与词嵌入类似，即定义一个位置嵌入矩阵$P\in {\mathbb{R}}^{L_{\max }\times d}$，其中$L_{\max }$是模型支持的最大序列长度，$d$是向量维度，在训练任务中更新参数。最终，位置嵌入将与词嵌入相加，共同作为词元的向量表示输入到Transformer解码器层中。

Transformer解码器层

GPT放弃了Transformer编码器双向全注意力的设计，完全基于解码器的单向掩码注意力，这是由于其主要任务为自回归生成，即从左到右逐词生成文本，在满足需求的同时还保证了架构简洁性。

Transformer解码器也是GPT实现上下文敏感的词表示的核心。由于其自回归性，输入的原始词表示在多层Transformer中能够通过自注意力权重捕捉到历史依赖信息，细化语义表示，而无需引入额外的模块显式标注上下文函数。

输出层

GPT的输出层由线性层和softmax操作构成。Transformer解码器最终将输出与词向量大小相同的向量${\mathbf{h}}_t\in {\mathbb{R}}^d$，线性层将该向量映射到词表空间${\mathbb{R}}^V$

$${\mathbf{z}}_t={\mathbf{W}}_o{\mathbf{h}}_t+{\mathbf{b}}_o$$

其中${\mathbf{W}}_o\in {\mathbb{R}}^{V\times d}$是可训练的权重矩阵，${\mathbf{b}}_o\in {\mathbb{R}}^V$为偏置项。${\mathbf{z}}_t$将由softmax归一化，计算下一个词元的概率分布。

任务无关性

GPT以生成任务为主的训练目标、大规模的参数与数据支撑和模型架构强大的依赖捕捉能力与自适应性是其能够实现任务无关的关键。通过在训练过程中对输入格式的设计，GPT能准确理解自然语言指令，将各类任务转化为生成任务，以下是一些案例：

任务类型	例子
文本续写	输入: “Once upon a time,” 输出: " there was a dragon…"
文本分类	输入: “判断情感: 这部电影很棒。→” 输出: “正面”
问答	输入: “问题: 地球半径是多少？上下文: 地球的平均半径为6371公里。→” 输出: “6371公里”
文本翻译	输入: “翻译英文到中文: Hello →” 输出: “你好”