主要参考学习资料及插图来源:
《机器人学导论(第4版)》John J.Craig著
台大机器人学之运动学——林沛群
本章前置知识:矢量和矩阵的四则运算-单位矩阵-转置矩阵-逆矩阵-分块矩阵
码字总结不易,求点赞收藏加关注(´•ω•̥`)
有问题欢迎评论区讨论~
目录
空间描述和变换2
复杂姿态描述
上一节我们用旋转矩阵来描述姿态,但仅限于绕其中一个主轴的单自由度旋转,且我们得知姿态描述中包含三个独立变量,接下来我们讨论如何用三个参数描述空间中的任意姿态
任何三自由度的旋转都可以拆解成三个单自由度的旋转,由于旋转不满足交换律,所以多次旋转的先后顺序需要明确定义。而旋转转轴也需要明确定义,围绕方向固定不动的参考坐标系主轴旋转的拆解方式称为固定角(Fixed Angles),围绕转动坐标系当下的主轴旋转的拆解方式称为欧拉角(Euler Angles)
X-Y-Z固定角
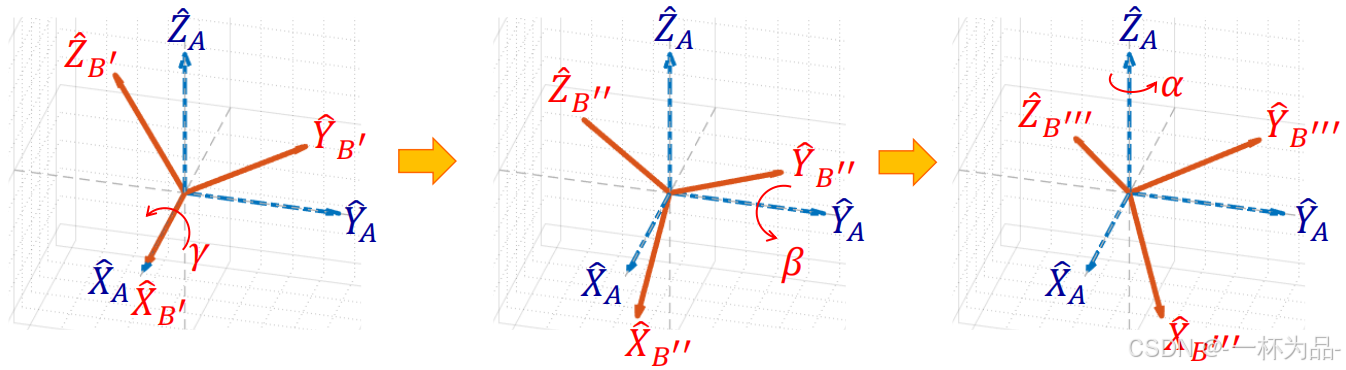
给定参考坐标系 { A } \{A\} {A}和我们要描述姿态的坐标系 { B } \{B\} {B},从固定角的视角来看,任意姿态的 { B } \{B\} {B}都可以由以下过程表示:将 { B } \{B\} {B}与 { A } \{A\} {A}重合,先绕 X ^ A \hat{X}_A X^A旋转 γ \gamma γ角,再绕 Y ^ A \hat{Y}_A Y^A旋转 β \beta β角,最后绕 Z ^ A \hat{Z}_A Z^A旋转 α \alpha α角得到最终的 { B } \{B\} {B},因而可以推导 { B } \{B\} {B}到 { A } \{A\} {A}的等价旋转矩阵: B A R X Y Z ( γ , β , α ) = R Z ( α ) R Y ( β ) R X ( γ ) = [ c α − s α 0 s α c α 0 0 0 1 ] [ c β 0 s β 0 1 0 − s β 0 c β ] [ 1 0 0 0 c γ − s γ 0 s γ c γ ] ^A_BR_{XYZ}(\gamma,\beta,\alpha)=R_Z(\alpha)R_Y(\beta)R_X(\gamma)=\begin{bmatrix}c\alpha&-s\alpha&0\\s\alpha&c\alpha&0\\0&0&1\end{bmatrix}\begin{bmatrix}c\beta&0&s\beta\\0&1&0\\-s\beta&0&c\beta\end{bmatrix}\begin{bmatrix}1&0&0\\0&c\gamma&-s\gamma\\0&s\gamma&c\gamma\end{bmatrix} BARXYZ(γ,β,α)=RZ(α)RY(β)RX(γ)= cαsα0−sαcα0001 cβ0−sβ010sβ0cβ 1000cγsγ0−sγcγ
(矩阵书写顺序与实际旋转操作顺序相反,从旋转一个矢量的角度来看,是因为旋转矩阵乘在矢量的左边,所以右侧的矩阵会先与矢量相乘)
(等价旋转矩阵下标表示绕主轴旋转的操作顺序,可以根据实际情况调换)
最终得到:
B A R X Y Z ( γ , β , α ) = [ c α c β c α c β s γ − s α c γ c α s β c γ + s α s γ s α c β s α s β s γ + c α c γ s α s β c γ − c α s γ − s β c β s γ c β c γ ] ^A_BR_{XYZ}(\gamma,\beta,\alpha)=\begin{bmatrix}c\alpha c\beta&c\alpha c\beta s\gamma-s\alpha c\gamma&c\alpha s\beta c\gamma+s\alpha s\gamma\\s\alpha c\beta&s\alpha s\beta s\gamma+c\alpha c\gamma&s\alpha s\beta c\gamma-c\alpha s\gamma\\-s\beta&c\beta s\gamma&c\beta c\gamma\end{bmatrix} BARXYZ(γ,β,α)= cαcβsαcβ−sβcαcβsγ−sαcγsαsβsγ+cαcγcβsγcαsβcγ+sαsγsαsβcγ−cαsγcβcγ ①
反过来,如果已知旋转矩阵各个元素的数值,逆求三个固定角,令
B A R X Y Z ( γ , β , α ) = [ r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ] ^A_BR_{XYZ}(\gamma,\beta,\alpha)=\begin{bmatrix}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{bmatrix} BARXYZ(γ,β,α)= r11r21r31r12r22r32r13r23r33
则
{ β = A t a n 2 ( − r 31 , r 11 2 + r 21 2 ) α = A t a n 2 ( r 21 c β , r 11 c β ) γ = A t a n 2 ( r 31 c β , r 33 c β ) \left\{\begin{matrix}\beta=\mathrm{Atan2}(-r_{31},\sqrt{r_{11}^2+r_{21}^2})\\ \alpha=\mathrm{Atan2}(\frac{r_{21}}{c\beta},\frac{r_{11}}{c\beta})\\ \gamma=\mathrm{Atan2}(\frac{r_{31}}{c\beta},\frac{r_{33}}{c\beta})\end{matrix}\right. ⎩ ⎨ ⎧β=Atan2(−r31,r112+r212)α=Atan2(cβr21,cβr11)γ=Atan2(cβr31,cβr33)
( β ≠ 9 0 ∘ ) (\beta\neq 90^{\circ}) (β=90∘)
(式中 A t a n 2 ( y , x ) = a r c t a n y x \mathrm{Atan2}(y,x)=arctan\frac{y}{x} Atan2(y,x)=arctanxy,即反正切函数的双参量表示法,可以根据 x x x和 y y y的符号判别角的象限,而单输入值的反正切函数无法区分)
上式中 cos β \cos\beta cosβ只考虑正根以得到单解来建立各种姿态表示法之间一一对应的映射函数,但在某些情况下有必要求出所有的解,会在第四章说明
如果 β = 9 0 ∘ \beta=90^{\circ} β=90∘,则只能求出 α \alpha α和 γ \gamma γ的和或差,在这种情况下一般取 α = 0 \alpha=0 α=0, γ = { A t a n 2 ( r 12 , r 22 ) ( β = 9 0 ∘ ) − A t a n 2 ( r 12 , r 22 ) ( β = − 9 0 ∘ ) \gamma=\left\{\begin{matrix}\mathrm{Atan2}(r_{12},r_{22})(\beta=90^{\circ})\\-\mathrm{Atan2}(r_{12},r_{22})(\beta=-90^{\circ})\end{matrix}\right. γ={Atan2(r12,r22)(β=90∘)−Atan2(r12,r22)(β=−90∘)
结合式①即可理解求解公式的推导
Z-Y-X欧拉角

给定参考坐标系 { A } \{A\} {A}和我们要描述姿态的坐标系 { B } \{B\} {B},从欧拉角的视角来看,任意姿态的 { B } \{B\} {B}都可以由以下过程表示:将 { B } \{B\} {B}与 { A } \{A\} {A}重合,先绕 Z ^ B \hat{Z}_B Z^B转 α \alpha α角得到 { B ′ } \{B'\} {B′},再绕 Y ^ B ′ \hat{Y}_{B'} Y^B′转 β \beta β角得到 { B ′ ′ } \{B''\} {B′′},最后绕 X ^ B ′ ′ \hat{X}_{B''} X^B′′转 γ \gamma γ角得到最终的 { B } \{B\} {B}(欧拉角选取转轴的顺序与固定角相反,原因会在下面解释)
借由 { B } \{B\} {B}的中间状态 { B ′ } \{B'\} {B′}和 { B ′ ′ } \{B''\} {B′′}和欧拉角的定义表达 B A R ^A_BR BAR,我们可以写出:
B A R = B ′ A R B ′ ′ B ′ R B B ′ ′ R ^A_BR=^A_{B'}R^{B'}_{B''}R^{B''}_{B}R BAR=B′ARB′′B′RBB′′R
即:
B A R X ′ Y ′ Z ′ ( γ , β , α ) = R Z ′ ( α ) R Y ′ ( β ) R X ′ ( γ ) = [ c α − s α 0 s α c α 0 0 0 1 ] [ c β 0 s β 0 1 0 − s β 0 c β ] [ 1 0 0 0 c γ − s γ 0 s γ c γ ] ^A_BR_{X'Y'Z'}(\gamma,\beta,\alpha)=R_{Z'}(\alpha)R_{Y'}(\beta)R_{X'}(\gamma)=\begin{bmatrix}c\alpha&-s\alpha&0\\s\alpha&c\alpha&0\\0&0&1\end{bmatrix}\begin{bmatrix}c\beta&0&s\beta\\0&1&0\\-s\beta&0&c\beta\end{bmatrix}\begin{bmatrix}1&0&0\\0&c\gamma&-s\gamma\\0&s\gamma&c\gamma\end{bmatrix} BARX′Y′Z′(γ,β,α)=RZ′(α)RY′(β)RX′(γ)= cαsα0−sαcα0001 cβ0−sβ010sβ0cβ 1000cγsγ0−sγcγ
相乘后得:
B A R X ′ Y ′ Z ′ ( γ , β , α ) = [ c α c β c α c β s γ − s α c γ c α s β c γ + s α s γ s α c β s α s β s γ + c α c γ s α s β c γ − c α s γ − s β c β s γ c β c γ ] ^A_BR_{X'Y'Z'}(\gamma,\beta,\alpha)=\begin{bmatrix}c\alpha c\beta&c\alpha c\beta s\gamma-s\alpha c\gamma&c\alpha s\beta c\gamma+s\alpha s\gamma\\s\alpha c\beta&s\alpha s\beta s\gamma+c\alpha c\gamma&s\alpha s\beta c\gamma-c\alpha s\gamma\\-s\beta&c\beta s\gamma&c\beta c\gamma\end{bmatrix} BARX′Y′Z′(γ,β,α)= cαcβsαcβ−sβcαcβsγ−sαcγsαsβsγ+cαcγcβsγcαsβcγ+sαsγsαsβcγ−cαsγcβcγ
我们发现,这个结果与以相反顺序绕固定轴旋转三次得到的结果完全相同,因而逆求解公式也相同
可以这样更深地理解固定角与欧拉角之间的关系:两种姿态描述方法不同的解释在于运用了旋转矩阵两种不同的作用,一是在同一个坐标系下旋转矢量,二是将矢量的坐标在不同坐标系之间变换。固定角是用前者描述 { A } \{A\} {A}的三个主轴矢量旋转到 { B } \{B\} {B}的过程,而欧拉角是用后者将在 { B } \{B\} {B}下的主轴矢量坐标一步步借由中间坐标系变换到 { A } \{A\} {A}
其他转角组合
在实际情况我们会遇到更多按不同顺序进行绕主轴的三个旋转,所有排列总共24种,固定角12种,欧拉角12种,都被称为转交排列设定法(需要注意第一次转动和最后一次转动绕同一个主轴也是一种排列,只要保证相邻两次切换围绕的主轴即可)
除此之外,姿态描述还有轴角表示法和四元数表示法,完全解释篇幅较长,若有余力我会写拓展专题
映射(Mapping)
映射是将矢量从一个坐标系投影到另一个坐标系的变换
坐标平移
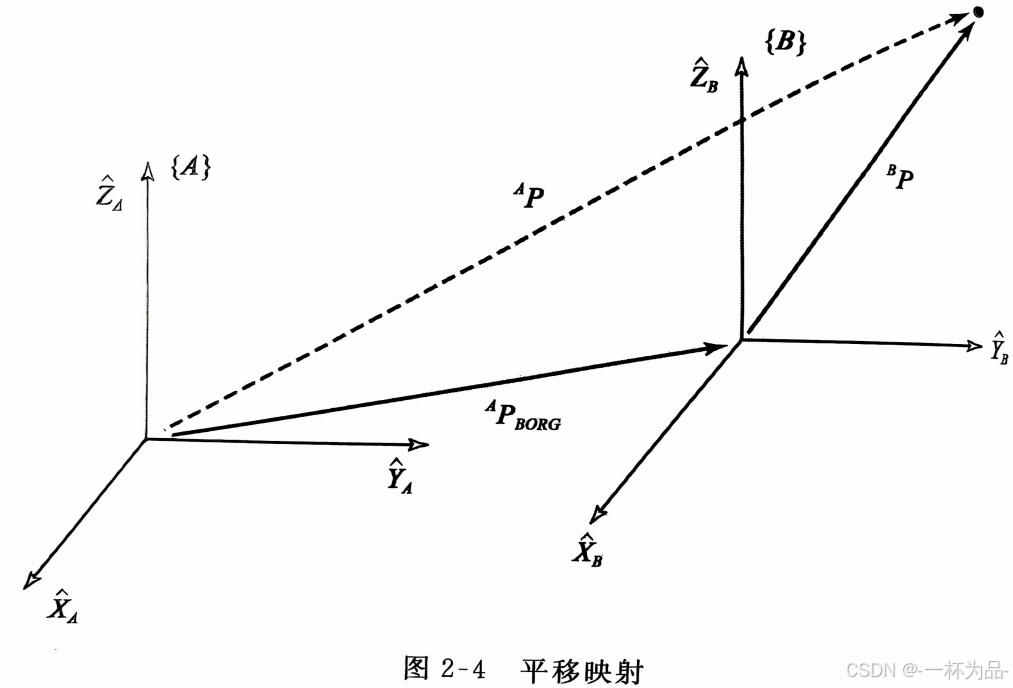
我们用矢量 A P B O R G ^AP_{BORG} APBORG表示 { B } \{B\} {B}的原点相对于 { A } \{A\} {A}的位置
当 { A } \{A\} {A}与 { B } \{B\} {B}姿态相同,位置不同时,由矢量加法的几何意义:
A P = B P + A P B O R G ^AP=^BP+^AP_{BORG} AP=BP+APBORG
坐标旋转
当 { A } \{A\} {A}与 { B } \{B\} {B}位置相同,姿态不同时,由上一篇所介绍的旋转矩阵转换矢量坐标的作用:
A P = B A R B P ^AP=^A_BR^BP AP=BARBP
一般变换
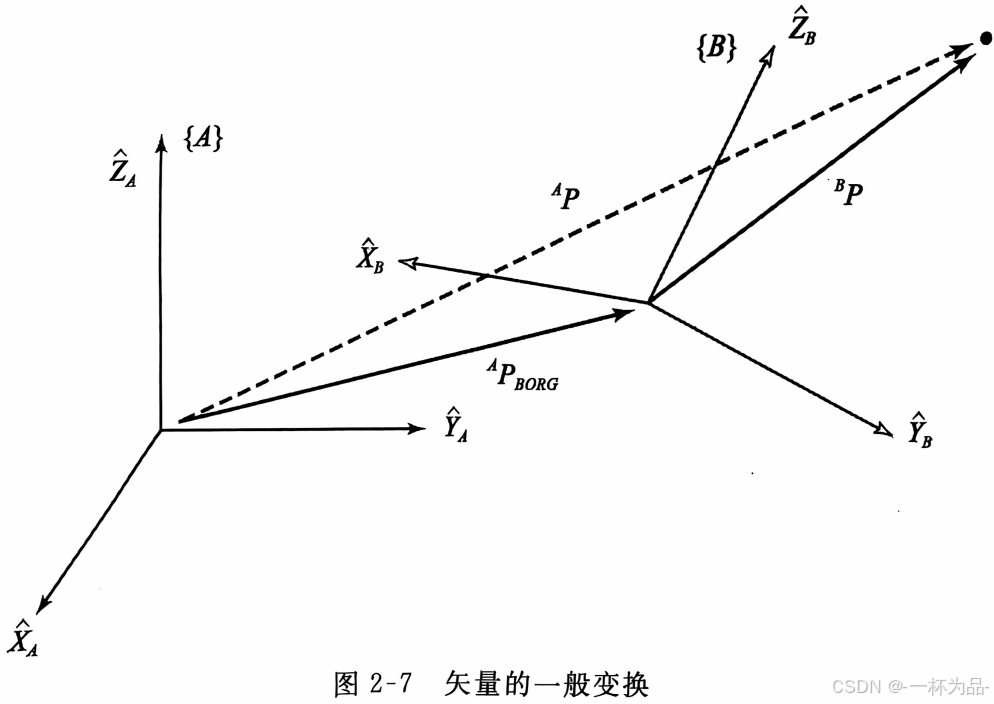
当 { A } \{A\} {A}与 { B } \{B\} {B}位置和姿态都不同时,可以先将 { B } \{B\} {B}旋转到和 { A } \{A\} {A}相同的姿态得到 { B ′ } \{B'\} {B′},以 { B ′ } \{B'\} {B′}为中间坐标系对 B P ^BP BP进行旋转变换,再作 { B ′ } \{B'\} {B′}到 { A } \{A\} {A}的平移变换:
A P = B A R B P + A P B O R G ^AP=^A_BR^BP+^AP_{BORG} AP=BARBP+APBORG②
为了简化算式,我们将平移和旋转整合起来,定义齐次变换矩阵:
B A T = [ B A R A P B O R G 0 T 1 ] ^A_BT=\begin{bmatrix}^A_BR&^AP_{BORG}\\\mathbf{0}^T&1\end{bmatrix} BAT=[BAR0TAPBORG1]
其中 0 T \mathbf{0}^T 0T表示三维零向量的转置
这样式②可写为:
[ A P 1 ] = [ B A R A P B O R G 0 T 1 ] [ B P 1 ] \begin{bmatrix}^AP\\1\end{bmatrix}=\begin{bmatrix}^A_BR&^AP_{BORG}\\\mathbf{0}^T&1\end{bmatrix}\begin{bmatrix}^BP\\1\end{bmatrix} [AP1]=[BAR0TAPBORG1][BP1]
这样我们就以一个简单的矩阵形式表示了一般变换的旋转和平移
复合变换
复合变换借用中间坐标系求解两坐标系的相对关系
例如已知 { C } \{C\} {C}相对于 { B } \{B\} {B},并且已知 { B } \{B\} {B}相对于 { A } \{A\} {A},已知 C P ^CP CP求 A P ^AP AP,可先将 C P ^CP CP变换成 B P ^BP BP再变换成 A P ^AP AP:
B P = C B T C P ^BP=^B_CT^CP BP=CBTCP
A P = B A T B P = B A T C B T C P ^AP=^A_BT^BP=^A_BT^B_CT^CP AP=BATBP=BATCBTCP
由此定义 C A P = B A T C B T ^A_CP=^A_BT^B_CT CAP=BATCBT
逆变换
已知 B A T ^A_BT BAT求 A B T ^B_AT ABT可以直接对 B A T ^A_BT BAT求逆矩阵,但还可以利用变换的性质
关于 A B T ^B_AT ABT的旋转变换,由旋转矩阵的性质可知 A B R = B A R T ^B_AR=^A_BR^T ABR=BART
关于 A B T ^B_AT ABT的平移变换,将 A P B O R G ^AP_{BORG} APBORG变换成 { B } \{B\} {B}中的描述: B ( A P B O R G ) = A B T A P B O R G = A B R A P B O R G + B P A O R G ^B(^AP_{BORG})=^B_AT^AP_{BORG}=^B_AR^AP_{BORG}+^BP_{AORG} B(APBORG)=ABTAPBORG=ABRAPBORG+BPAORG
上式左侧为零,可得: B P A O R G = − A B R A P B O R G = − B A R T A P B O R G ^BP_{AORG}=-^B_AR^AP_{BORG}=-^A_BR^T{}^AP_{BORG} BPAORG=−ABRAPBORG=−BARTAPBORG
由此 A B T = [ A B R T − B A R T A P B O R G 0 T 1 ] = B A T − 1 ^B_AT=\begin{bmatrix}^B_AR^T&-^A_BR^T{}^AP_{BORG}\\\mathbf{0}^T&1\end{bmatrix}=^A_BT^{-1} ABT=[ABRT0T−BARTAPBORG1]=BAT−1
变换方程

图中 { D } \{D\} {D}可以用两种不同的方式表达成变换相乘的方式:
D U T = A U T D A T ^U_DT=^U_AT^A_DT DUT=AUTDAT
D U T = B U T C B T D C T ^U_DT=^U_BT^B_CT^C_DT DUT=BUTCBTDCT
两个表达式构造成一个变换方程:
A U T D A T = B U T C B T D C T ^U_AT^A_DT=^U_BT^B_CT^C_DT AUTDAT=BUTCBTDCT
如有 n n n个未知变换和 n n n个变换方程,变换可由变换方程解出。设上式中所有变换除了 C B T ^B_CT CBT外均已知,可解出:
C B T = B U T − 1 A U T D A T D C T − 1 ^B_CT=^U_BT^{-1}{}^U_AT^A_DT^C_DT^{-1} CBT=BUT−1AUTDATDCT−1
算子(Operator)
算子是对矢量进行平移和旋转操作的变换
B A T ^A_BT BAT除了变换以外,也可以充当算子对矢量或点进行平移或转动
平移算子
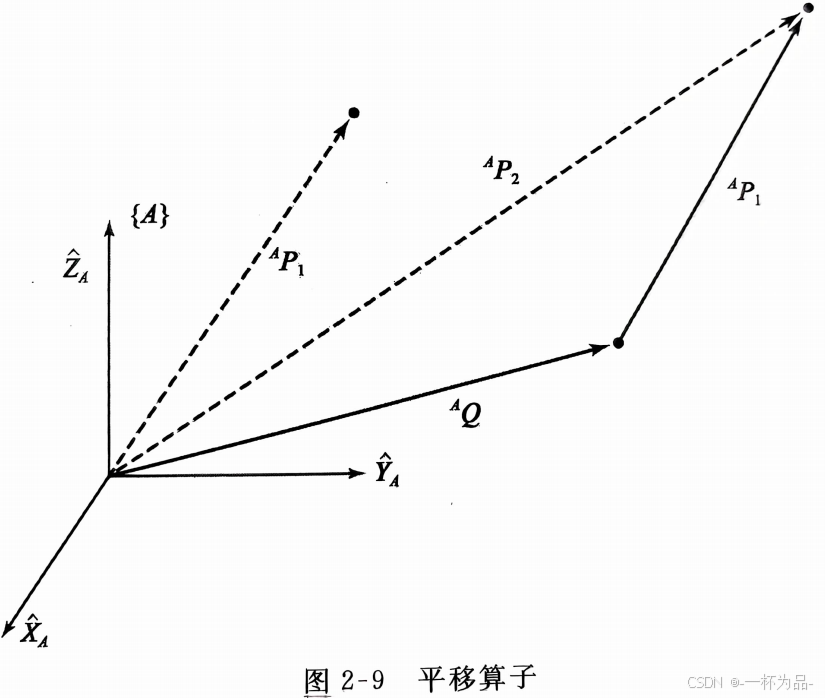
将 A P 1 ^AP_1 AP1指向的点沿 A Q ^AQ AQ进行平移得到一个新的矢量 A P 2 ^AP_2 AP2,计算如下:
A P 2 = A P 1 + A Q ^AP_2=^AP_1+^AQ AP2=AP1+AQ
用矩阵算子写出平移变换,有:
A P 2 = D ( Q ) A P 1 ^AP_2=D(Q)^AP_1 AP2=D(Q)AP1
算子 D Q D_Q DQ可以被看成是一个特殊形式的齐次变换:
D ( Q ) = [ I A Q 0 T 1 ] D(Q)=\begin{bmatrix}I&^AQ\\\mathbf{0}^T&1\end{bmatrix} D(Q)=[I0TAQ1]
旋转算子
由上一篇所介绍的旋转矩阵描述刚体转动状态的作用,可以得到旋转算子的定义:将矢量 A P 1 ^AP_1 AP1用旋转 R R R变换成一个新的矢量 A P 2 ^AP_2 AP2
当一个旋转矩阵作为算子时无需写出上下标,因为不涉及两个坐标系,但我们将用另一个符号说明是绕哪个轴旋转的,写成:
A P 2 = R K ( θ ) A P 1 ^AP_2=R_K(\theta)^AP_1 AP2=RK(θ)AP1
符号 R K ( θ ) R_K(\theta) RK(θ)是一个旋转算子,表示绕 K ^ \hat{K} K^轴旋转 θ \theta θ角度,例如绕 Z ^ \hat{Z} Z^轴旋转 θ \theta θ的算子:
R z ( θ ) = [ c θ − s θ 0 0 s θ c θ 0 0 0 0 1 0 0 0 0 1 ] R_z(\theta)=\begin{bmatrix}c\theta&-s\theta&0&0\\s\theta&c\theta&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} Rz(θ)= cθsθ00−sθcθ0000100001
变换算子
与一般变换一样,将平移和旋转整合起来我们得到通用的变换算子。因为只涉及一个坐标系,所以没有上下标。算子 T T T将矢量 A P 1 ^AP_1 AP1平移并旋转得到一个新矢量: A P 2 = T A P 1 ^AP_2=T^AP_1 AP2=TAP1
齐次变换矩阵
源于旋转矩阵在上一篇所讲的三个作用,在这一篇我们也探索出了齐次变换矩阵的三个作用:
1.描述位姿: B A T ^A_BT BAT表示 { B } \{B\} {B}相对于 { A } \{A\} {A},其中 B A R ^A_BR BAR的各列是定义 { B } \{B\} {B}主轴方向的单位矢量, A P B O R G ^AP_{BORG} APBORG确定了 { B } \{B\} {B}的原点
2.变换映射: B A T ^A_BT BAT是映射 B P → A P ^BP\rightarrow^AP BP→AP
3.变换算子: B A T ^A_BT BAT将 A P 1 ^AP_1 AP1变换为 A P 2 ^AP_2 AP2
本章我们只考虑了位置矢量的变换,而速度矢量和力矢量由于类型不同,它们的变换形式也不同,将在第五章讨论
本章完






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








