Jzzhu has a big rectangular chocolate bar that consists of n × m unit squares. He wants to cut this bar exactly k times. Each cut must meet the following requirements:
- each cut should be straight (horizontal or vertical);
- each cut should go along edges of unit squares (it is prohibited to divide any unit chocolate square with cut);
- each cut should go inside the whole chocolate bar, and all cuts must be distinct.
The picture below shows a possible way to cut a 5 × 6 chocolate for 5 times.
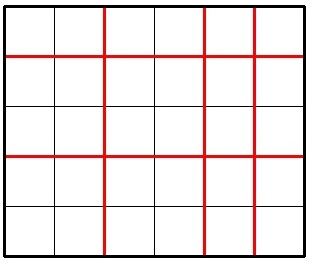
Imagine Jzzhu have made k cuts and the big chocolate is splitted into several pieces. Consider the smallest (by area) piece of the chocolate, Jzzhu wants this piece to be as large as possible. What is the maximum possible area of smallest piece he can get with exactly k cuts? The area of a chocolate piece is the number of unit squares in it.
A single line contains three integers n, m, k (1 ≤ n, m ≤ 109; 1 ≤ k ≤ 2·109).
Output a single integer representing the answer. If it is impossible to cut the big chocolate k times, print -1.
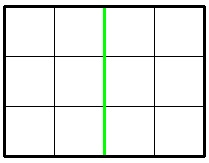
3 4 1
6
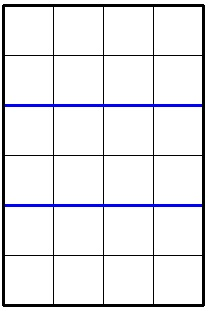
6 4 2
8
2 3 4
-1
In the first sample, Jzzhu can cut the chocolate following the picture below:
In the second sample the optimal division looks like this:
In the third sample, it's impossible to cut a 2 × 3 chocolate 4 times.
题意:一个n*m的矩阵巧克力,沿着直线将其切上k次,问切出面积最小的块最大可以是多少。
题解:由于数据范围很大,刚开始我想到的是沿着一条边二分找到最大的值。后来不行,又用了三分,还是错了。比赛时就没有搞出来,赛后看了大牛陈立杰的代码,真是屌。这题貌似也不可以用三分解决。纯手工暴力枚举加贪心,不过小技巧用得很好,当一边最小的行切成,可以有多种切法,直接跳到以最多的切线来切出同样的行,然后剩下几刀分配给竖着切的面,这样可以使最大。屌屌屌屌屌。
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <queue>
#include <map>
#include <stack>
#include <list>
#include <vector>
using namespace std;
#define LL __int64
int main()
{
LL n,m,k,ans;
scanf("%I64d%I64d%I64d",&n,&m,&k);
if ((n-1)+(m-1)<k)
{
printf("-1\n");
return 0;
}
ans=0;
for (int i=1;i<=n;i++)
{
int h=n/(n/i);
i=h;
if (m-1<(k-i+1)) continue;
LL l=max(k-i+2,1LL);
ans=max(ans,(n/i*(m/l))) ;
}
printf("%I64d\n",ans);
return 0;
}






 本文探讨了一种高效策略,用于确定在指定次数切割后,从一个长宽分别为n*m单位格的巧克力中,可以获得的最小面积块的最大可能值。通过算法优化,实现了复杂数据范围内的快速计算,提供了解决类似切割问题的实用方法。
本文探讨了一种高效策略,用于确定在指定次数切割后,从一个长宽分别为n*m单位格的巧克力中,可以获得的最小面积块的最大可能值。通过算法优化,实现了复杂数据范围内的快速计算,提供了解决类似切割问题的实用方法。
















 1325
1325

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








