AcWing1052提高课dp系列状态机模型

状态机 + kmp

你现在需要设计一个密码 S，S 需要满足：

S 的长度是 N；
S 只包含小写英文字母；
S 不包含子串 T；
例如：abc 和 abcde 是 abcde 的子串，abd 不是 abcde 的子串。

请问共有多少种不同的密码满足要求？

由于答案会非常大，请输出答案模 109+7 的余数。

输入格式
第一行输入整数N，表示密码的长度。

第二行输入字符串T，T中只包含小写字母。

输出格式
输出一个正整数，表示总方案数模 109+7 后的结果。

数据范围
1≤N≤50,
1≤|T|≤N，|T|是T的长度。

输入样例1：
2
a
输出样例1：
625
输入样例2：
4
cbc
输出样例2：
456924

设f[i][j]表示当前已经生成密码的第i位，且第i位在模式串t中能匹配到的位置为j的方案数

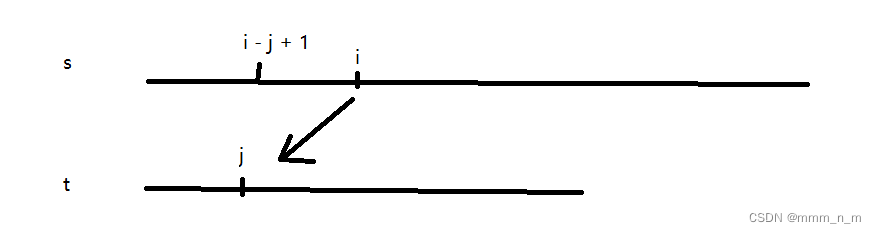
这表示从s[i - j + 1]到 s[i] 与t[1] 到 t[j] 的这一段两个字符串相等，假设t的长度为len
那么当j==len时，生成的密码不合法，所以在状态转移的过程中，j不能转移到len

那么如何描述状态的转移呢
假设第i + 1位能匹配到在t中的位置为u，通过kmp算法，我们可以找到这个位置u
那么f[i][j]能转移到f[i + 1][u],所以从f[i][j]这一条边到f[i + 1][u]这条路径存在，
那么f[i + 1][u] += f[i][j]

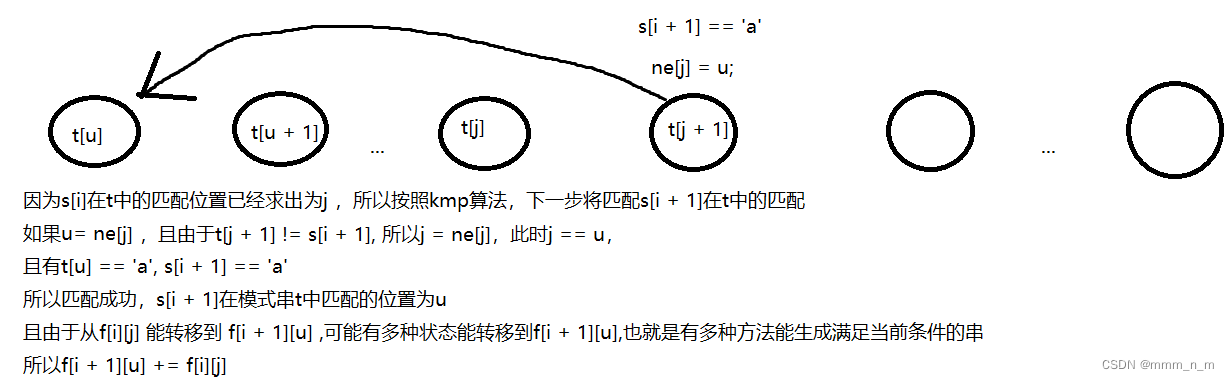
在图中假设的是s[i + 1] == ‘a’的情况，在实际运行中我们需要考虑s[i + 1]是所有小写字母的情况
所以需要枚举s[i + 1]从’a’到’z’
最后的答案从定义上可知是f[n][0~len - 1]之和

#include <iostream>
#include <cstring>
using namespace std;

const int N = 55, mod = 1e9 + 7;
int f[N][N];
char t[N];
int ne[N];
int n;

int main(){
    cin >> n;
    cin >> t + 1;
    int len = strlen(t + 1);
    
    // kmp模板
    for(int i = 2, j = 0; i <= n; i ++){
        while(j && t[i] != t[j + 1]) j = ne[j];
        if(t[i] == t[j + 1]) j ++;
        ne[i] = j;
    }
    f[0][0] = 1;//当前密码生成0位，在t中匹配位置为0，方案为一个（初始化）
    for(int i = 0; i < n; i ++){
        for(int j = 0; j < len; j ++){
            for(int k = 'a'; k <= 'z'; k ++){//枚举第i + 1位为'a'到'z'的情况
                int u = j;
                while(u && t[u + 1] != k) u = ne[u];
                if(k == t[u + 1]) u ++;//找到第i + 1位在t中所能匹配到的位置
                
                if(u < len) f[i + 1][u] = (f[i + 1][u] + f[i][j]) % mod;
                //答案需要对1e9+7取模
            }
        }
    }
    int res = 0;
    for(int i = 0; i < len; i ++) res = (res + f[n][i]) % mod;
    cout << res << endl;
    return 0;
    
}

感谢指正