数据结构进阶(一)稀疏矩阵

分享一下我老师大神的人工智能教程！零基础，通俗易懂！http://blog.youkuaiyun.com/jiangjunshow

也欢迎大家转载本篇文章。分享知识，造福人民，实现我们中华民族伟大复兴！

               

稀疏矩阵

一、稀疏矩阵的定义

      对于那些零元素数目远远多于非零元素数目，并且非零元素的分布没有规律的矩阵称为稀疏矩阵（sparse）。

      人们无法给出稀疏矩阵的确切定义，一般都只是凭个人的直觉来理解这个概念，即矩阵中非零元素的个数远远小于矩阵元素的总数，并且非零元素没有分布规律。

二、稀疏矩阵的压缩存储

      由于稀疏矩阵中非零元素较少，零元素较多，因此可以采用只存储非零元素的方法来进行压缩存储。

      由于非零元素分布没有任何规律，所以在进行压缩存储的时侯需要存储非零元素值的同时还要存储非零元素在矩阵中的位置，即非零元素所在的行号和列号，也就是在存储某个元素比如a_ij的值的同时，还需要存储该元素所在的行号i和它的列号j，这样就构成了一个三元组(i,j,a_ij)的线性表。

      三元组可以采用顺序表示方法，也可以采用链式表示方法，这样就产生了对稀疏矩阵的不同压缩存储方式。

a、稀疏矩阵的顺序实现

      若把稀疏矩阵的三元组线性表按顺序存储结构存储，则称为稀疏矩阵的三元组顺序表。

      顺序表中除了存储三元组外，还应该存储矩阵行数、列数和总的非零元素数目，这样才能唯一的确定一个矩阵。

 

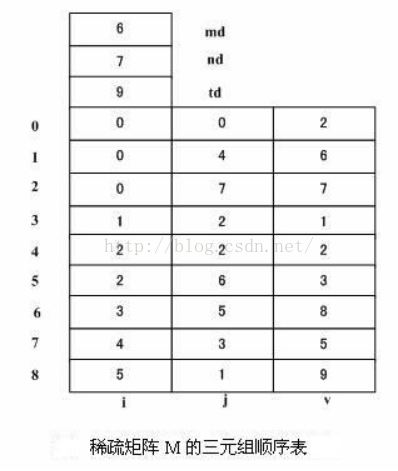
　　顺序存储结构存储三元组线性表的C#代码如下：

    struct tupletype<T>    {        public int i;//行号        public int j;//列号        public T v; //元素值        public tupletype(int i, int j, T v)        {            this.i = i;            this.j = j;            this.v = v;        }    }    class spmatrix<T>    {        int MAXNUM;//非零元素的最大个数        int md;//行数值     &n