链表

CS-Notes

相交链表

#160
设 两条链表分别为A,B;
若两条链表有交点，
A的长度为a+c，B的长度为b+c，其中 c 为尾部公共部分长度，可知 a + c + b = b + c + a。

当访问 A 链表的指针访问到链表尾部时，下一个结点为null,令它从链表 B 的头部开始访问链表 B；同样地，当访问 B 链表的指针访问到链表尾部时，令它从链表 A 的头部开始访问链表 A。这样就能控制访问 A 和 B 两个链表的指针能同时访问到交点。

如果不存在交点，那么 a + b = b + a，以下实现代码中 l1 和 l2 会同时为 null，从而退出循环。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode l1 = headA,l2 = headB;
        while(l1 != l2){
        //写法一
            l1 = (l1 == null) ? headB : l1.next;
            l2 = (l2 == null) ? headA : l2.next;
        //写法二
            if(l1 == null){
                l1 = headB;
            }else{
                l1 = l1.next;//尾结点后为null
            }
            if(l2 == null){
                l2 = headA;
            }else{
                l2 = l2.next;
            }
        }
        return l1;
    }
}

反转整个链表

#206
Reverse a singly linked list.

Example:

Input: 1->2->3->4->5->NULL
Output: 5->4->3->2->1->NULL

法一：用栈

class Solution {
    public ListNode reverseList(ListNode head) {
        if(head == null)
            return null;//不加这句，执行可以，提交不行，应该是没考虑到特殊情况
        Stack<ListNode> s = new Stack<>();
        while(head.next != null){
            s.push(head);
            head = head.next;
        }//head此时指向尾结点，入栈尾结点之前的所有结点
        ListNode l = head;//需要返回链表头结点
        while(!s.empty()){
            head.next = s.pop();
            head = head.next;
        }
        head.next = null;// 别忘了链表末尾要指向null
        return l;
    }
}

法二：迭代法

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode next = null;//下一个结点，用来让head迭代
        ListNode prev = null;//前一个结点
        while(head != null){
            next = head.next;
            head.next = prev;
            prev = head;
            head = next;
        }
        return prev;//最后next和head都是null
    }
}

法三：递归法
知乎参考讲解

class Solution {
    public ListNode reverseList(ListNode head) {
       //空链表或单个结点，反转它自己
       if(head == null || head.next == null){
           return head;
       }//base case
        ListNode last = reverseList(head.next);
        head.next.next = head;
        head.next = null;
        return last;
    }
}

反转链表前N个结点

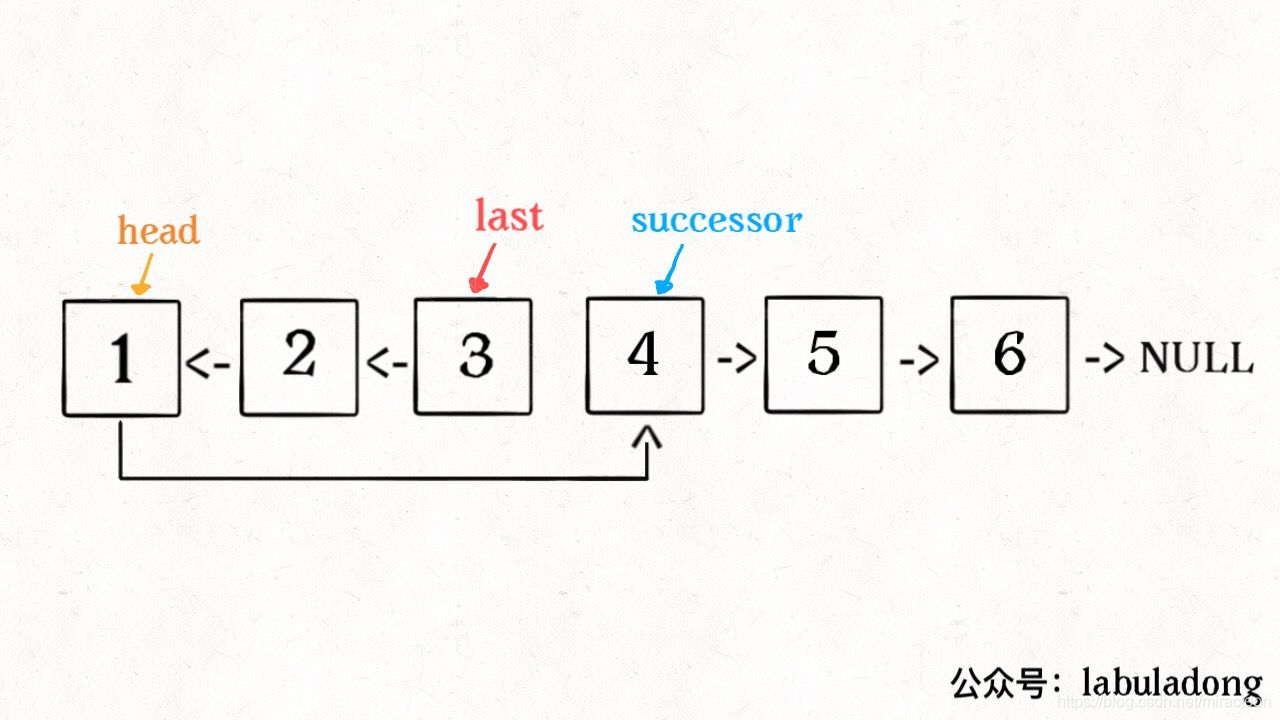
比如说对于下图链表，执行 reverseN(head, 3)：

class Solution {
    ListNode successor = null;
    public ListNode reverseListN(ListNode head,int n) {
    // 记录第 n + 1 个节点
       if(n == 1){
       	successor = head.next;
       	return head;
    }
     // 以 head.next 为起点，需要反转前 n - 1 个节点
    ListNode last = reverseListN(head.next,n-1);
    head.next.next = head;
    // 让反转之后的 head 节点和后面的节点连起来
    head.next = successor;
    return last;
}

反转链表一部分

#92
给一个索引区间 [m,n]（索引从 1 开始），仅仅反转区间中的链表元素。

ListNode reverseBetween(ListNode head, int m, int n)

如果 m != 1 怎么办？如果我们把 head 的索引视为 1，那么我们是想从第 m 个元素开始反转对吧；如果把 head.next 的索引视为 1 呢？那么相对于 head.next，反转的区间应该是从第 m - 1 个元素开始的；那么对于 head.next.next 呢……

• 递归法

ListNode reverseBetween(ListNode head, int m, int n) {
    // base case
    if (m == 1) {
        return reverseN(head, n);
    }
    // 前进到反转的起点触发 base case
    head.next = reverseBetween(head.next, m - 1, n - 1);
    return head;
}

• python

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    # successor = None

    def reverseBetween(self, head: ListNode, left: int, right: int) -> ListNode:
        self.successor = None
        if left == 1:
            return self.reverseN(head, right)
        head.next = self.reverseBetween(head.next, left - 1, right - 1)
        return head
        
    def reverseN(self, node, n):
        if n == 1:
            self.successor = node.next
            return node
        last = self.reverseN(node.next, n - 1)
        node.next.next = node
        node.next = self.successor
        return last

• 迭代法
• 添加一个哑结点作为辅助，该结点位于列表头部。哑结点用来简化某些极端情况，例如列表中只含有一个结点，或需要删除列表的头部。

class Solution {
    public ListNode reverseBetween(ListNode head, int m, int n) {
        ListNode dummyHead = new ListNode(-1);
        dummyHead.next = head;// 用来返回头结点
        ListNode pre = dummyHead;
        //遍历到m-1位置
        for(int k = 1;k < m;k++){
            pre = pre.next;
        }
        //套用反转整个链表模板
        ListNode prev = null;
        ListNode cur = pre.next;
        for(int i = m; i <= n; i++){
            ListNode next = cur.next;
            cur.next = prev;
            prev = cur;
            cur = next;
        }
        //修改m和n-m位置处的结点的指向
        pre.next.next = cur;
        pre.next = prev;
        return dummyHead.next;//返回链表头结点
    }
}

25 k个一组翻转链表

# @lc code=start
# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseKGroup(self, head: ListNode, k: int) -> ListNode:
        if not head:
            return None
        lNode = rNode = head
        # base case 不足 k 个结点，保持原样
        for i in range(k):
            if not rNode:
                return head
            rNode = rNode.next
        newHead = self.reverse(lNode, rNode)
        lNode.next = self.reverseKGroup(rNode, k)
        return newHead

    # [left, right) 左闭右开区间
    # self 不能缺少
    def reverse(self, left, right):
        pre = ListNode()
        cur = left
        pre.next = cur
        while cur != right:
            nextNode = cur.next
            cur.next = pre
            pre = cur
            cur = nextNode
        return pre
# @lc code=end

合并两个有序链表

Example:

Input: 1->2->4, 1->3->4
Output: 1->1->2->3->4->4

leetcode#21

• 迭代法

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode dummyHead = new ListNode(-1);
        ListNode cur = dummyHead;
        while(l1 != null && l2 != null){
            if(l1.val < l2.val){
                cur.next = l1;
                cur = cur.next;
                l1 = l1.next;
            }else{
                cur.next = l2;
                cur = cur.next;
                l2 = l2.next;
            }
        }
        // 任一为空，直接连接另一条链表
        if(l1 == null){
            cur.next = l2;
        }else{
            cur.next = l1;
        }
        return dummyHead.next;
    }
}

• 递归法
  两个链表头部值较小的一个节点与剩下元素的 merge 操作结果合并

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if(l1 == null){
            return l2;
        }
        if(l2 == null){
            return l1;
        }
        if(l1.val < l2.val){
            l1.next = mergeTwoLists(l1.next,l2);
            return l1;
        }else{
            l2.next = mergeTwoLists(l1,l2.next);
            return l2;
        }
        
    }
}

删除排序链表中的重复元素

leetcode#83

• 普通法

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        ListNode cur = head;
        while(cur != null && cur.next != null){
            ListNode next = cur.next;
            if(cur.val == next.val){
                cur.next = next.next;
            }else{
                cur = cur.next;
            }  
        }
        return head;
    }
}

• 递归
  递归套路解决链表问题：
  • 找终止条件：当head指向链表只剩一个元素的时候，自然是不可能重复的，因此return
  • 想想应该返回什么值：应该返回的自然是已经去重的链表的头节点
  • 每一步要做什么：宏观上考虑，此时head.next已经指向一个去重的链表了，而根据第二步，我应该返回一个去重的链表的头节点。因此这一步应该做的是判断当前的head和head.next是否相等，如果相等则说明重了，返回head.next，否则返回head

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
       if(head == null || head.next == null){
           return head;
       }
        head.next = deleteDuplicates(head.next);
        if(head.val == head.next.val){
            head = head.next;
        }
        return head;
    }
}

或者

class Solution {
class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head == null || head.next == null) return head;
        if (head.val == head.next.val) 
        	head = deleteDuplicates(head.next);
        else 
        	head.next = deleteDuplicates(head.next);
        return head;
    }
}

删除排序链表中的重复元素II

力扣82
题目描述：给定一个排序链表，删除所有含有重复数字的节点，只保留原始链表中 没有重复出现 的数字。

1.  1——>1——>1——>2(null)
2.  1——>2——>2——>3——>3——>4(null)

递归法

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head == null || head.next == null) return head;
        if (head.val == head.next.val){
        	//情况1  移动 head 直到出现值不相等的情况
            while (head.next != null && head.val == head.next.val){
                head.next = head.next.next;
            }
            //此时 head 依然是重复的值，向右再移动一次
            head = deleteDuplicates(head.next);
        }else {
            //2
            head.next = deleteDuplicates(head.next);
        }
        return head;
    }
}

非递归

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head == null || head.next == null) return head;
        ListNode pre = new ListNode(-1);
        pre.next = head;
        ListNode cur = pre;//哑结点,可以合并一开始就有重复元素的情况
        ListNode fast = head;
        while (fast != null){
            if (fast.next != null && fast.val == fast.next.val){
                while (fast.next != null && fast.next.val == fast.val){
                    fast = fast.next;
                }
                //此时 fast 指向的依然是重复元素，往后再移一位
                cur.next = fast.next;
                fast = fast.next;
            }else {
                cur = cur.next;
                fast = fast.next;
            }
        }
        return pre.next;
    }
}

删除链表的倒数N个结点

leetcode#19

• 双指针法

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(-1);
        dummy.next = head;
        ListNode fast = dummy;
        ListNode slow = dummy;
        //相隔n+1个结点
        for(int i = 0; i <= n; i++){
            fast = fast.next;
        }
        while(fast != null){
            fast = fast.next;
            slow = slow.next;
        }
        slow.next = slow.next.next;
        return dummy.next;//有些情况会把head删掉，所以不能返回head
    }
}

• 两次遍历算法

删除从列表开头数起的第 (L - n + 1)个结点，其中 LL是列表的长度。只要我们找到列表的长度 L，这个问题就很容易解决。
我们把第 (L - n) 个结点的 next 指针重新链接至第 (L - n + 2) 个结点

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        ListNode first = head;
        int length = 0;
        while(first != null){
            length++;
            first = first.next;
        }
        length -= n;
        first = dummy;
        while(length > 0){
            length--;
            first = first.next;
        }
        first.next = first.next.next;
        return dummy.next;
    }
}

两两交换链表中的结点

leetcode#24
Example:

Given 1->2->3->4, you should return the list as 2->1->4->3.

• 迭代

class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        ListNode pre = dummy;
        while(pre.next != null && pre.next.next != null){
            ListNode l1 = pre.next;
            ListNode l2 = pre.next.next;
            ListNode next = l2.next;
            //交换
            l1.next = next;
            l2.next = l1;
            pre.next = l2;
            //迭代
            pre = l1;
        }
        return dummy.next;
    }
}

• 递归

class Solution {
    public ListNode swapPairs(ListNode head) {
        if(head == null || head.next == null){
            return head;
        }
        ListNode l1 = head;
        ListNode l2 = head.next;
        l1.next = swapPairs(l2.next);
        l2.next = l1;
        //此时l2变成了头结点
        return l2;
    }
}

关于递归的题： 判断平衡二叉树

leetcode#110

a binary tree in which the left and right subtrees of every node
differ in height by no more than 1.

• 自顶向下（暴力法）: 先序遍历 + 判断深度

class Solution {
    private int height(TreeNode root){
        if(root == null){
            return 0;
        }
        return Math.max(height(root.left),height(root.right)) + 1;
    }
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        return Math.abs(height(root.left) - height(root.right)) < 2 
            && isBalanced(root.left) && isBalanced(root.right);
    }
}

针对满二叉树，设共有 n 层，第 i 层有 2^i-1个结点，全部结点个数为 2ⁿ- 1，设总结点个数为 N,则最后一层结点个数为 2^n-1=(N+1)/2

• 自底向上：后序遍历 + 剪枝

class Solution {
    private boolean isB = true;
    public boolean isBalanced(TreeNode root) {
        height(root);
        return isB;
    }
    private int height(TreeNode root){
        if(root == null) return 0;
        int left = height(root.left);
        int right = height(root.right);
        if(Math.abs(left - right) > 1) isB = false;
        return Math.max(left,right) + 1;//返回结点深度
    }
}

复杂度分析：
时间复杂度 O(N)： N为树的节点数；最差情况下，需要递归遍历树的所有节点。
空间复杂度 O(N)： 最差情况下（树退化为链表时），系统递归需要使用 O(N)的栈空间。

两数相加II（两条链表相加）

leetcode445
示例：

输入：(7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 8 -> 0 -> 7

• 法一：利用两个栈存储两条链表每个结点的值

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        Stack<Integer> s1 = new Stack<>();
        Stack<Integer> s2 = new Stack<>();
        int carry = 0;
        ListNode head = new ListNode(0);
         while(l1 != null){
             s1.push(l1.val);
             l1 = l1.next;
         }
         while(l2 != null){
             s2.push(l2.val);
             l2 = l2.next;
         }
         //链表头结点值相加可能产生进位
        while(!s1.isEmpty() || !s2.isEmpty() || carry != 0){
            int x = s1.isEmpty() ? 0 : s1.pop();
            int y = s2.isEmpty() ? 0 : s2.pop();
            int sum = x + y + carry;
            carry = sum / 10;//进位
            ListNode node = new ListNode(sum % 10);
            node.next = head.next;//若声明head = null,这里出错
            head.next = node;
        }
        return head.next;
    }
}

• 法二： 尝试反转链表

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode n1 = reverse(l1);
        ListNode n2 = reverse(l2);
        int carry = 0;
        ListNode dummy = new ListNode(0);
        ListNode pre = dummy;
        
        while(n1 != null || n2 != null || carry != 0){
            int x = n1 == null ? 0 : n1.val;
            int y = n2 == null ? 0 : n2.val;
            int sum = x + y + carry;
            carry = sum / 10;
            ListNode n3 = new ListNode(sum % 10);
            pre.next = n3;
            pre = pre.next;
            n1 = n1 == null ? null : n1.next;
            n2 = n2 == null ? null : n2.next;
        }
        return reverse(dummy.next);
    }
    //反转链表
    private ListNode reverse(ListNode head){
        if(head == null || head.next == null){
            return head;
        }
        ListNode last = reverse(head.next);
        head.next.next = head;
        head.next = null;
        return last;
    }
}

• 法三：递归
  • 如果len1与len2都为1，那么当前的值应为(l1.val+l2.val）%10,进位更新为(l1.val+l2.val）/10；
  • 如果len1大于len2，递归计算（l1.next,l2），当前的值应为（l1.val+进位）%10，进位更新为（l1.val+进位）/10；
  • 如果len1等于len2，递归计算（l1.next,l2.next）,当前的值应为（l1.val+进位+l2.val）%10，进位更新为（l1.val+进位+l2.val）/10；
  • 返回当前节点的指针
  • 递归结束

为方便递归，递归开始前我们保证len1>=len2，另外递归结束后若进位为1，需要新建值为1的头节点

class Solution {
    private int carry = 0;
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        
        ListNode n1 = l1,n2 = l2;
        int len1 = 0,len2 = 0;
        while(l1 != null){
            l1 = l1.next;
            len1++;
        }
        while(l2 != null){
            l2 = l2.next;
            len2++;
        }
        ListNode node = (len1 > len2) ? add(n1,n2,len1,len2) : add(n2,n1,len2,len1);
        if(carry != 0){
            ListNode pre = new ListNode(1);
            pre.next = node;
            return pre;
        }
        return node;
    }
    private ListNode add(ListNode l1,ListNode l2,int len1,int len2){
        int temp = 0;
        if(len1 == 1 && len2 == 1){
            temp = l1.val;
            l1.val = (temp + l2.val) % 10;
            carry = (temp + l2.val) / 10;
            return l1;
        }
        if(len1 > len2){
            l1.next = add(l1.next,l2,len1 - 1,len2);
            temp = l1.val;
            l1.val = (temp + carry)% 10;
            carry = (temp + carry) / 10;
            return l1;
        }
        l1.next = add(l1.next,l2.next,len1 - 1,len2 - 1);
        temp = l1.val;
        l1.val = (temp + l2.val + carry) % 10;
        carry = (temp + l2.val + carry) / 10;
        return l1;
    }
}

回文链表

leetcode234

Example 1:

Input: 1->2
Output: false

Example 2:

Input: 1->2->2->1
Output: true

Example 3:
Input:1->2->1
Output: true

• 法一：暴力法(不推荐)
  反转整个链表，观察反转的链表和原链表是否完全相同

class Solution {
    public boolean isPalindrome(ListNode head) {
        ListNode node = head;
        ListNode cur = copy(head);
        ListNode last = reverse(head);
        while(cur != null && last != null){
            if(cur.val != last.val) return false;
            cur = cur.next;
            last = last.next;
        }
        return true;   
    }
   //递归实现复制单链表
    private ListNode copy(ListNode head){
        if(head == null) return null;
        ListNode newNode = new ListNode(head.val);
        newNode.next = copy(head.next);
        return newNode;
    }
    private ListNode reverse(ListNode head){
        if(head == null || head.next == null){
            return head;
        }
        ListNode last = reverse(head.next);
        head.next.next = head;
        head.next = null;
        return last;
    }
}

• 法二：快慢指针（推荐）
  
  

class Solution {
    public boolean isPalindrome(ListNode head) {
        if(head == null || head.next == null) return true;
        ListNode slow = head,fast = head;
        ListNode cur = null,prev = null;
        while(fast != null && fast.next != null){
            cur = slow;
            slow = slow.next;
            fast = fast.next.next;
            cur.next = prev;
            prev = cur;
        }
        if(fast != null){
            slow = slow.next;
        }
        while(cur != null && slow != null){
            if(cur.val != slow.val) return false;
            cur = cur.next;
            slow = slow.next;
        }
        return true;
    }
}

分隔链表

leetcode725

Input:
root = [1, 2, 3, 4, 5, 6, 7], k = 5
Output: [[1,2], [3,4], [5],[6],[7]]
Explanation:
The input has been split into consecutive parts with size difference at most 1, and earlier parts are a larger size than the later parts.

以上面的例子为例，mod = 7 % 5 = 2，size = 7 / 5 = 1,让前面两个数组元素储存的结点个数为1 + 1，剩下三个储存结点个数为1,
注：迭代时要让每一段的尾结点后连接NULL

class Solution {
    public ListNode[] splitListToParts(ListNode root, int k) {
        ListNode[] list = new ListNode[k];
        // int length = count(root);
        int length = 0;
        ListNode cur = root;
        while(cur != null){
            length++;
            cur = cur.next;
        }
        
        int mod = length % k;
        int size = length / k;
        for( int i = 0; root != null && i < k; i++){
            list[i] = root;
            int curSize = size + (mod-- > 0 ? 1 : 0);//实际每段长度
            for(int j = 1; j < curSize; j++){
                root = root.next;
            }
            //让每一段的尾结点后接NULL
            ListNode temp = root.next;
            root.next = null;
            root = temp;
        }
        return list;
    }
    //递归计算链表长度
    // private int count(ListNode root){
    //     return root==null?0:count(root.next)+1;
    // }
}

链表元素按奇偶聚集

leetcode328

Example 1:

Input: 1->2->3->4->5->NULL
Output: 1->3->5->2->4->NULL

Example 2:

Input: 2->1->3->5->6->4->7->NULL
Output: 2->3->6->7->1->5->4->NULL

双指针

class Solution {
    public ListNode oddEvenList(ListNode head) {
        if(head == null){
            return head;
        }
        ListNode odd = head,even = head.next,node = even;
        while(even != null && even.next != null){
            ListNode n1 = odd.next.next;
            ListNode n2 = even.next.next;
            odd.next = n1;
            even.next = n2;
            odd = n1;
            even = n2;
        }
        odd.next = node;
        return head;
    }
}

旋转链表

Example 1:

Input: 1->2->3->4->5->NULL, k = 2
Output: 4->5->1->2->3->NULL
Explanation:
rotate 1 steps to the right: 5->1->2->3->4->NULL
rotate 2 steps to the right: 4->5->1->2->3->NULL

Example 2:

Input: 0->1->2->NULL, k = 4
Output: 2->0->1->NULL
Explanation:
rotate 1 steps to the right: 2->0->1->NULL
rotate 2 steps to the right: 1->2->0->NULL
rotate 3 steps to the right: 0->1->2->NULL
rotate 4 steps to the right: 2->0->1->NULL

leetcode61

class Solution {
    public ListNode rotateRight(ListNode head, int k) {
        if(head == null || head.next == null){
            return head;
        }
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        ListNode pre = dummy;
        int length = 0;
        while(head != null){
            head = head.next;
            pre = pre.next;
            length++;
        }
        //首尾相连
        pre.next = dummy.next;
        int n = k / length + 1;
        int N = n * length - k;//新的头结点位置,也可以看作倒数第k % length个结点，倒数第0个是原头结点，倒数第一个是原尾结点
        while(N-- > 0){
            pre = pre.next;
        }
        head = pre.next;
        pre.next = null;
        return head;
    }
}