Factorization Machine 学习笔记

FM 的 优点：

1. 解决了特征稀疏的问题，能在非常系数数据的情况下进行预估。
2. 解决了特征组合的问题，研究了特征与特征之间的向量，不像LR线性回归那样没有组合
3. FM使一个通用模型，适用于大部分场景，而其他因式分解模型只能用于一些输入数据比较固定的情况
4. 训练速度快，线性复杂度是线性的，优化效果很好

一般的线性回归：

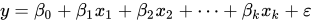
考虑了特征组合：

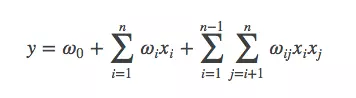
缺点：复杂度太高，复杂度n^2，wij只能在xi，xj不同时为0的情况下训练，特征稀疏的情况下，大多数情况下xi，xj大多数情况下为0，训练不充分

FM的推导：
引入一个变量$V_i$，让$V_i$等于
$$V_i=(v_{i1},v_{i2},v_{i3},...,v_{ik}{)}^T$$
所以当 i =1或者n时：
$$V_1=(v_{11},v_{12},v_{13},...,v_{1k}{)}^T$$
$$V_n=(v_{n1},v_{n2},v_{n3},...,v_{nk}{)}^T$$
已知$w_{ij}$可以组成一个矩阵：
$$W={\left[\begin{array}{cccc}{w}_{11}& w_{12}& ...& w_{1n}\\ w_{21}& w_{22}& ...& w_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ w_{n1}& w_{n2}& ...& w_{nn}\end{array}\right]}_{nn}$$
而$V_i$组成一个矩阵$V$：
$$V=\left[\begin{array}{c}{V_1}^T\\ {V_2}^T\\ ⋮\\ {V_n}^T\end{array}\right]={\left[\begin{array}{cccc}{v}_{11}& v_{12}& ...& v_{1k}\\ v_{21}& v_{22}& ...& v_{2k}\\ ⋮& ⋮& \ddots & ⋮\\ v_{n1}& v_{n2}& ...& v_{nk}\end{array}\right]}_{nk}$$
所以可以有$V{V}^T=W$

所以可以得到一个FM的推导公式：

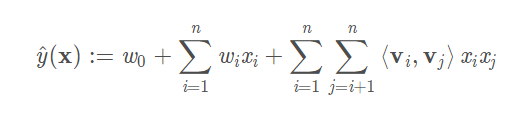
其中，点积可以写成

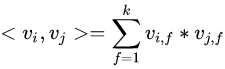
所以原公式又可以写成


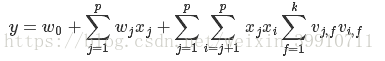
复杂度只n, k有关，所以这个FM的复杂度是nk，是线性复杂度，相对较小

拓展，FFM