热题系列章节4

470. 用 Rand7() 实现 Rand10()

给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数，试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。

你只能调用 rand7() 且不能调用其他方法。请不要使用系统的 Math.random() 方法。
每个测试用例将有一个内部参数 n，即你实现的函数 rand10() 在测试时将被调用的次数。请注意，这不是传递给 rand10() 的参数。

示例 1:
输入: 1
输出: [2]

示例 2:
输入: 2
输出: [2,8]

示例 3:
输入: 3
输出: [3,8,10]

提示:
1 <= n <= 105

class Solution:
    def rand10(self):
        while True:
            num = (rand7() - 1) * 7 + rand7()  # // 等概率生成[1,49]范围的随机数
            if num <= 40:                      #// 拒绝采样，并返回[1,10]范围的随机数
                return num % 10 + 1

48. 旋转图像

给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。

说明：
你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
举例：
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],

原地旋转输入矩阵，使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]

题干解析：
n*n的矩阵 旋转90度意味着 第一行变为第n列 第n行变成第1列。
先将矩阵的行列转置，（只遍历半个矩阵，以i==j 为判断）再将第一列与第n列调换 第2列与第n-1列调换，以此类推（调换时 只调换一半，否则重复调换相当于调换）。

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix) #len(二维数组) 返回列表第一维长度
        #n = len(matrix[0]) #返回列表第二维长度
        
        for i in range(n):  #将矩阵转置
            for j in range(n):
                if i != j: #若无这句 翻转多次等于无翻转
                    temp = matrix[i][j]
                    matrix[i][j] = matrix[j][i]
                    matrix[j][i] = temp
                else:
                    break
        for i in range(n):
            for j in range(n//2):
                    res = matrix[i][j]
                    matrix[i][j] = matrix[i][n-1-j]
                    matrix[i][n-1-j] = res

34. 在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]。
时间复杂度要求：O ( log ⁡ n ) O(\log n)O(logn)

示例 1：
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：
输入：nums = [], target = 0
输出：[-1,-1]

示例 4：
输入：nums =[5,7,7,8,8,10], target = 4或11
输出：[-1,-1]

二分查找左边界：找不到返回-1
nums[mid] == target则right = mid - 1继续往左逼近，其他与二分查找没有区别
举例可知，能找到target的情况下，跳出循环时nums[left]=target 是其左边界，返回left即可
换个角度理解为什么left是最终的左边界而不是right：在能找到target也就是存在nums[mid]=target的情况时，right = mid-1，那么while退出时必然right不可能是target了【直接举个例子更清晰】
找不到target的情况下，跳出循环时nums[left] != target，令left = -1返回

二分查找右边界：找不到返回-1
nums[mid] == target则left = mid + 1继续往左逼近，其他不变
举例可知，能找到target的情况下，跳出循环时nums[right]=target是其右边界，返回right即可
找不到target的情况下，nums[right] != target，令right = -1返回

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
		# 返回情况2.2 2.3
        if not nums or nums[0] > target or nums[-1] < target:
            return [-1, -1]
        else:    # 返回情况 1， 2.1    
            left_border = self.binary_search_left_border(nums, target, 0, len(nums)-1)
            right_border = self. binary_search_right_border(nums, target, 0, len(nums)-1)
            return [left_border, right_border]
        

    def binary_search_left_border(self, nums, target, left, right) -> int:
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                right = mid - 1 # 向左逼近
            elif nums[mid] > target:
                right = mid - 1
            else:
                left = mid + 1
        if nums[left] == target:
            return left
        else:
            return -1

    def binary_search_right_border(self, nums, target, left, right) -> int:
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                left = mid + 1 # 向右逼近
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
        if nums[right] == target:
            return right
        else:
            return -1

64. 最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
本题思路为创建输入相同大小的辅助矩阵，辅助矩阵中每个位置不依赖其他位置，仅仅依赖上上两个步骤，选择更少的一步最终到达位置即为最小和（辅助矩阵为各个位置最小和）

class Solution:
    def minPathSum(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        if grid == None :
            return 0
        if len(grid)==0 or len(grid[0])==0:
            return sum(grid)
        
        row = len(grid)
        loc = len(grid[0])
        dp = grid
        for i in range(1,row):
            dp[i][0] = dp[i-1][0] + grid[i][0]
        for i in range(1,loc):
            dp[0][i] = dp[0][i-1] + grid[0][i]
        for i in range(1,row):
            for j in range(1,loc):
                dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])
        
        return dp[i][j]

394. 字符串解码

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

s = "3[a]2[bc]", 返回 "aaabcbc".
s = "3[a2[c]]", 返回 "accaccacc".
s = "2[abc]3[cd]ef", 返回 "abcabccdcdcdef".

在上面的例子中，第二个示例出现了括号内嵌的情况。本题中，比较难处理的也是这部分。

在本篇幅中，我们使用栈的思路，来解决本题。上面提及出现的括号内嵌的情况，当我们返回的时候，要从内部往外去生成与拼接字符，这也是我们使用栈的原因，因为栈具有先入后出的特性。

在这里，我们栈里面，每项需要存储两个信息，一个是左括号前面的字符，一个是左括号前面的数字。

例如示例 2，3[a2[c]]，其中 a2[c] 这一部分，入栈时应该是这样的：(‘a’, 2)，后面会遍历字符 c，遇到右括号的时候，要进行出栈操作。弹出的元素 (‘a’, 2)，这里要跟字符 c 拼接称新的字符串 a + 2 * ‘c’，也就是 acc。

具体的做法：

遍历元素为数字时，将数字字符转换为数字，这里用于后面字符解码倍数运算；
遍历元素为字母时，这个时候，直接将字符加在结果尾部；
遍历元素为左括号时，要将左括号前面的字母和数字进行入栈，入栈之后，要将存储这两项的变量重置；
遍历元素为右括号时，进行出栈，拼接字符。

class Solution:
    def decodeString(self, s: str) -> str:
        # 辅助栈，每项存储两个信息，一个左括号前面的字符，一个左括号前面的数字
        stack = []
        mult = 0
        ans = ''

        for char in s:
            # 当字符为数字字符时，转换为数值，用于后续倍数运算
            if char.isdigit():
                # mult = int(char)
                # 这里要注意数字位数，
                # 上面的写法，遇到用例 "100[leetcode]" 出错了，这里改为
                mult = mult * 10 + int(char)
            # 遇到左括号时，将前面的字符和数值入栈
            elif char == '[':
                stack.append((ans, mult))
                # 这里要重置存储这两项的变量
                ans = ''
                mult = 0
            # 遇到右括号时，出栈
            elif char == ']':
                front_char, cur_mult = stack.pop()
                ans = front_char + cur_mult * ans
            # 这里表示遇到的是字符，直接添加到 ans 末尾
            else:
                ans += char

        return ans

221. 最大正方形

题目：
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例：

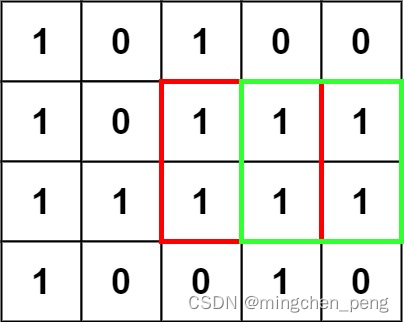
输入：
matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：4

思路：
动态规划

定义一个动态矩阵，其中每个位置表示以当前位置为右下角，能够得到的最大正方形的边长。
初始化为全0,然后遍历矩阵，当遍历位置的数为0时直接跳过即可。

当遍历位置的数为1时，才能作为正方形的右下角，然后判断。
如果遍历的位置是第一行或者第一列，那能取到的最大变长就是1。
在其他位置的话，就由当前位置向上看，向左看，向对角线方向看，连续是1的长度是多少，取这三个方向中的最小的长度，因为能构成的正方形边长取决于最小的，然后再加上当前位置的1,得到边长。
更新结果中的最大边长，最后返回边长的平方，即面积。

class Solution(object):
    def maximalSquare(self, matrix):
        """
        :type matrix: List[List[str]]
        :rtype: int
        """
        m = len(matrix)
        if m == 0:
            return 0
        n = len(matrix[0])
        dp = [[0]* n for _ in range(m)]
        ans = 0
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == '1':
                    if i == 0:
                        dp[i][j] = 1
                    elif j == 0:
                        dp[i][j] = 1
                    else :
                        dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]) + 1
                    ans = max(ans,dp[i][j])
        return ans * ans  

240. 搜索二维矩阵 II

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

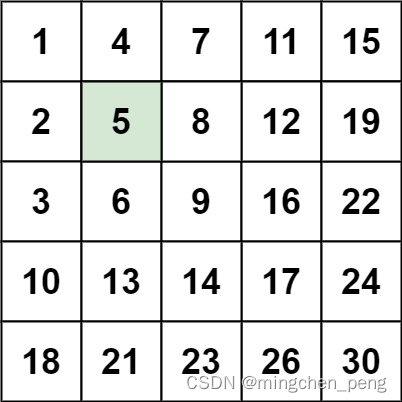
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

思路：
按照矩阵的规律来遍历矩阵，从左到右，从上到下都是递增的数组，可以从左下角开始遍历，正好等于目标值就返回True,如果比目标值大就往上面一行遍历，如果比目标值小就往右边的列遍历，直到遍历到行或者列的边界，还是没有找到目标值，就返回False。

时间复杂度为O(n+m)。

class Solution(object):
    def searchMatrix(self, matrix, target):
        """
        :type matrix: List[List[int]]
        :type target: int
        :rtype: bool
        """
        m = len(matrix)
        if m == 0: return False
        n = len(matrix[0])
        i,j = m-1,0 # 从左下角开始找
        while i >= 0 and j < n:
            if matrix[i][j] == target:
                return True
            if matrix[i][j] > target:
                i -= 1 # 这个数大，后面的更大，往上一行找
            else:
                j += 1 # 这个数小，往右边这一个列找
        return False

162. 寻找峰值

峰值元素是指其值大于左右相邻值的元素。

给定一个输入数组 nums，其中 nums[i] ≠ nums[i+1]，找到峰值元素并返回其索引。

数组可能包含多个峰值，在这种情况下，返回任何一个峰值所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞。

class Solution:
    def findPeakElement(self, nums: List[int]) -> int:
        l = 0
        r = len(nums) -1
        while(l<r):
            mid = l + r >> 1
            if nums[mid] > nums[mid+1]:  # 当mid大于mid+1的时候,在[0,mid]一定存在一个峰值
                r = mid
            else:   # 当 nums[mid]<= nums[mid+1]时,由题相邻元素不等，就是nums[mid]  <=nums[mid+1]，则在[mid+1,len(nums)]一定有一个峰值，峰值不唯一但由于题目只要输出任意一个就可以，所以这样做。
                l = mid + 1
        return r 

当nums[mid]大于nums[mid+1]的时候,在[0,mid]一定存在一个峰值？？？？

因为如果nums[mid]不是峰值的话,nums[mid-1]就要大于nums[mid]，同理如果nums[mid-1]不是峰值的话,nums[mid–2]就要大于nums[mid-1]，就是保证不能出现拐点，但是这样下去，0一定时拐点，因为nums[-1] = -∞,所以在[0,mid]一定存在一个峰值。

14. 最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀，返回空字符串 “”。

示例 1：
输入：strs = [“flower”,“flow”,“flight”]
输出：“fl”

示例 2：
输入：strs = [“dog”,“racecar”,“car”]
输出：“”
解释：输入不存在公共前缀。

class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        def lcp(str1, str2):
            min_len = min(len(str1), len(str2))
            idx = 0

            while idx < min_len and str1[idx] == str2[idx]:
                idx += 1
            return str1[:idx]

        if not strs:
            return ''

        prefix = strs[0]

        for i in range(1, len(strs)):
            prefix = lcp(prefix, strs[i])

            if not prefix:
                break

        return prefix

234. 回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为
回文链表
。如果是，返回 true ；否则，返回 false

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def isPalindrome(self, head: Optional[ListNode]) -> bool:
        
        if head==None or head.next==None:
            return True

        if head.next.next == None:
            return head.val == head.next.val

        def rev(node):
            pre = None
            cur = node
            while cur:
                tmp = cur.next
                cur.next = pre
                pre = cur
                cur = tmp    
            return pre
        
        half1 = head
        slow, fast = head, head

        while fast.next and fast.next.next:
            slow = slow.next
            fast = fast.next.next
        
        half2 = rev(slow.next)

        while half2.next:
            if half1.val != half2.val:
                return False
            half1 = half1.next
            half2 = half2.next
        return half1.val == half2.val

补充题：手撕堆排序

def heapify(arr, n, i):
    largest = i  # 初始化最大值为根节点
    l = 2 * i + 1  # 左子节点的索引
    r = 2 * i + 2  # 右子节点的索引
 
    # 如果左子节点存在且大于根节点
    if l < n and arr[i] < arr[l]:
        largest = l
 
        # 如果右子节点存在且大于当前最大值
    if r < n and arr[largest] < arr[r]:
        largest = r
 
        # 如果最大值不是根节点
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # 交换
        print(arr,'@')  # 对每次处理过程进行输出并标记
 
        # 递归地调整受影响的子堆
        heapify(arr, n, largest)
 
 
def heap_sort(arr):
    n = len(arr)  # 获取列表长度
 
    # 构建最大堆，将数据调整为最大堆结构
    for i in range(n//2-1, -1, -1):
        heapify(arr, n, i)
        print(arr,'*')
 
    # 一个个从堆中取出元素
    print('--------------------')
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # 交换
        heapify(arr, i, 0)  # 将交换数据后的arr列表调整为最大堆，确保每一步都是最大堆数据结构
        print(arr,'-')
 
 
# 测试堆排序函数
arr = [1, 2, 3, 5, 6, 7]
heap_sort(arr)
print("排序后的数组:")
print(arr)

https://blog.youkuaiyun.com/2202_75561400/article/details/136232650