DenseNet

• 论文链接：https://arxiv.org/pdf/1608.06993.pdf
• 论文题目：Densely Connected Convolutional Network

DenseNet

Abstract

最近的研究表明如果在接近输入和输出的层加入一些捷径连接那么可以让网络更深，得到更好的结果，且还可以更有效的训练。在本文中，我们就遵循这个观点然后引出DenseNet，在前向传递的时候，它的每一层都要与其他层连接。在传统的卷积神经网络中L层就有L个连接——连接着自己和下一层——我们的网络有$\frac{L(L+1)}{2}$个连接。对于每一层来说，所有之前层的特征图都会被当做输入，然后自己生成的特征图也会被后面所有的层拿来作为输入。DenseNet有以下一些优点：它继续减弱了梯度消失所带来的影响，加强了特征的传播，引入了特征的重复利用，并且减少了参数的个数。我们对我们提出的结构在4个高度竞争的目标识别任务中进行了评估。DenseNet在大多数上都取得了state-of-the-art的结果。

1.Introduction

在本文中，我们提出结构：为了确保层之间信息流的最大化，我们直接将所有层互相连接起来。为了保存前向传递的本质，每一层从前面的所有层获得额外输入，然后将自己学习到的特征图输出到后续的所有层。图1展示了这个结构。不像ResNet，我们不会在卷积之前将特征通过相加的方式来结合（这里指的是ResNet捷径连接是通过相加来结合特征的），相反我们是通过拼接来结合特征。因此，第l层就有l个输入。

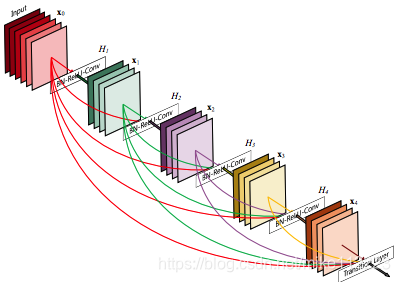
图1. 一个五层的dense模块，growth rate为4.

DenseNet的一个可能比较反直觉的地方是相比于传统的卷积神经网络，它的参数个数反而更少，这其实是因为不需要对多余的特征图进行重学习。传统的前向结构可以被视为一个带有状态的算法，这个状态是逐层传递的。每层从前一层读取这个状态然后再将状态写到下一层，即改变了状态同时也传递了需要保存的信息。ResNets更是显式地通过额外的恒等映射来保存了信息。近期的ResNet的变体发现其实很多层的贡献是非常小的，在训练时是可以随机drop掉的。这使得ResNets的状态其实跟RNN比较相似了，但是ResNets的参数个数多了很多。我们的提出的DenseNet结构显式的区分了添加的信息与需要保存的信息。DenseNet层是非常窄的（例如，每层12个滤波器），再额外加上一个很小特征图集合到整个网络的"collective knowledge"里，然后保持余下的特征图不变——最后的分类器是基于网络的所有特征图来做决策的。
除了更好的参数有效性（也就是使用参数更少），另一个DenseNet的大优点就是增强了网络的信息和梯度的传递（流动），使得网络更容易被训练。每一层都直接与损失函数和原始输入信号的梯度接触。除此之外，我们发现密集连接还带有一点泛化效果，这减少了对于小数据集的过拟合。

2.Related Work

DenseNet并不是从极深或者极广的网络结构中求取强大的特征表征能力，而是通过特征的复用来开发网络的潜能，这样得到的网络容易训练且参数有效性高。通过将不同层学到的特征图拼接起来来增加对于后续层的输入的变化，从而提高效率。这构成了ResNets和DenseNets的主要区别。

3.DenseNets

考虑通过卷积网络的一张图${\mathbf{x}}_0$。网络由L层组成，每一层都执行一个非线性的变换$H_l(\cdot )$，这里$l$表示层下标。$H_l(\cdot )$表示一系列操作的集合如BN,ReLU,Pool,Conv。我们将第$l$层的输出标记为${\mathbf{x}}_l$。

ResNets. 传统的卷积前向网络直接将第$l$层的输出作为第$l+1$层的输入，也就是${\mathbf{x}}_l=H_l({\mathbf{x}}_{l-1})$。ResNets增加了一个跳跃连接通过一个恒等映射绕过了非线性变换：
$${\mathbf{x}}_l=H_l({\mathbf{x}}_{l-1})+{\mathbf{x}}_{l-1}\text{\hspace{1em}(1)}$$
ResNets的一个优势就是梯度可以通过恒等映射的分支从后面的层流向前面的层。然后，恒等函数和$H_l$的输出是通过相加的方式结合的，这可能阻碍了网络中信息的流动。
Dense connectivity. 为了进一步增加层与层之间信息的流动，我们提出一种不同的连接方式：我们引入了对于前面所有层的直接连接，如图1。因此，第$l$层收到来自前面所有层的特征图，${\mathbf{x}}_0,...,{\mathbf{x}}_{l-1}$作为输入：
$${\mathbf{x}}_l=H_l([{\mathbf{x}}_0,{\mathbf{x}}_1,...,{\mathbf{x}}_{l-1}])\text{\hspace{1em}(2)}$$
这里$[{\mathbf{x}}_0,{\mathbf{x}}_1,...,{\mathbf{x}}_{l-1}]$表示前面层生成的特征图的拼接。

Composite function. 我们定义$H_l(\cdot )$为以下三个操作构成的复合函数：先BN，再ReLU，再Conv（ResNet的顺序和这里不一样，具体大家去原文找对应文章来阅读吧）。

Pooling layers. 方程2中用到的拼接操作，如果特征图大小不同那么是不可行的。然而，卷积神经网络一个很重要的部分就是降采样层来改变特征图大小。为了便于降采样，我们将我们的网络分成多个密集连接的dense block；如图2。我们将模块之间的层叫做过渡层（transition layers），做卷积和池化。我们实验中所使用到的过渡层是BN,1x1的conv和2x2的average pool。

图2. 一个带有3个dense模块的深度DenseNet。两个相邻模块间的层被称作过渡层，使用卷积和池化来改变特征图大小。

Growth rate. 如果每个方程$H_l$都生成k个特征图，那么接下来的第$l$层就有$k_0+k\times (l-1)$个输入特征图，$k_0$代表输入层的通道数。关于ResNet和DenseNet一个重要的区别就是DenseNet的层很窄也就是通道数少（如k=12）。我们将参数k定义为网络的增长率(growth rate)。在实验中，我们发现相对小的growth rate足够获得state-of-the-art的结果。对于这个现象的一个解释就是每一层都能得到该模块中所有前面层的特征图，因此，可以直接接触到网络的全部信息（collective knowledge）。可以将这些特征图作为网络的一个全局状态，每一层都将自己的k个特征图的信息加入到这个全局状态中。这个增长率就控制了每一层有多少新的信息加入到全局状态中。这个全局状态，一旦被写入，就可以在网络中任何地方都拿到，这和传统的网络结构不同，不需要一层一层的重复。

Bottleneck layers. 尽管每一层都只有k个输出特征图，但是它拥有很多的输入。在之前的研究中就提到使用1x1卷积来作为一个瓶颈层在3x3卷积之前减少输入特征图的数量来提高计算效率。我们使用BN-ReLU-Conv(1x1)-BN-ReLU-Conv(3x3)的$H_l$（DenseNet-B）。在实验中，1x1卷积生成4k的特征图。

Compression. 为了提高模型的紧凑性（减少参数），我们可以减少过渡层特征图的数量。如果一个dense模块拥有m张特征图，我们让接下来的过渡层生成$\lfloor \theta m\rfloor$张特征图，这里$0<\theta \le 1$被定义为压缩因子。当压缩因子为1时，表示经过过渡层的特征图数量保持不变。我们定义带有$\theta <1$的DenseNet为DenseNet-C，在我们的实验中，设置$\theta =0.5$。如果瓶颈和压缩都使用的话，模型就为DenseNet-BC。

Implementation Details. 在除了ImageNet的数据集上，我们使用三个dense模块，每个模块拥有相同层数。在进入第一个dense模块之前，对输入图像进行卷积输出16通道。对于3x3的卷积来说，我们会对每个边进行补0来保证特征图大小不变。我们在两个连续的dense模块之间使用1x1卷积接2x2平均池化作为过渡层。在最后一个dense模块的最后，链接全局平均池化和softmax分类器。三个dense模块的特征图大小分别是32x32，16x16，8x8。基础DenseNet结构配置 { L = 40 , K = 12 } , { L = 100 , K = 12 } , { L = 100 , K = 24 } \{L=40,K=12\},\{L=100,K=12\},\{L=100,K=24\} {L=40,K=12},{L=100,K=12},{L=100,K=24}。对于DenseNet-BC，网络配置是 { L = 100 , K = 12 } , { L = 250 , K = 24 } , { L = 190 , K = 40 } \{L=100,K=12\},\{L=250,K=24\},\{L=190,K=40\} {L=100,K=12},{L=250,K=24},{L=190,K=40}。

在ImageNet上，我们使用DenseNet-BC结构，4个dense模块，输入图像224x224。初始卷积层，7x7，步长为2，输出2k维。所有特征图的数量都来自于设定k。如表1。

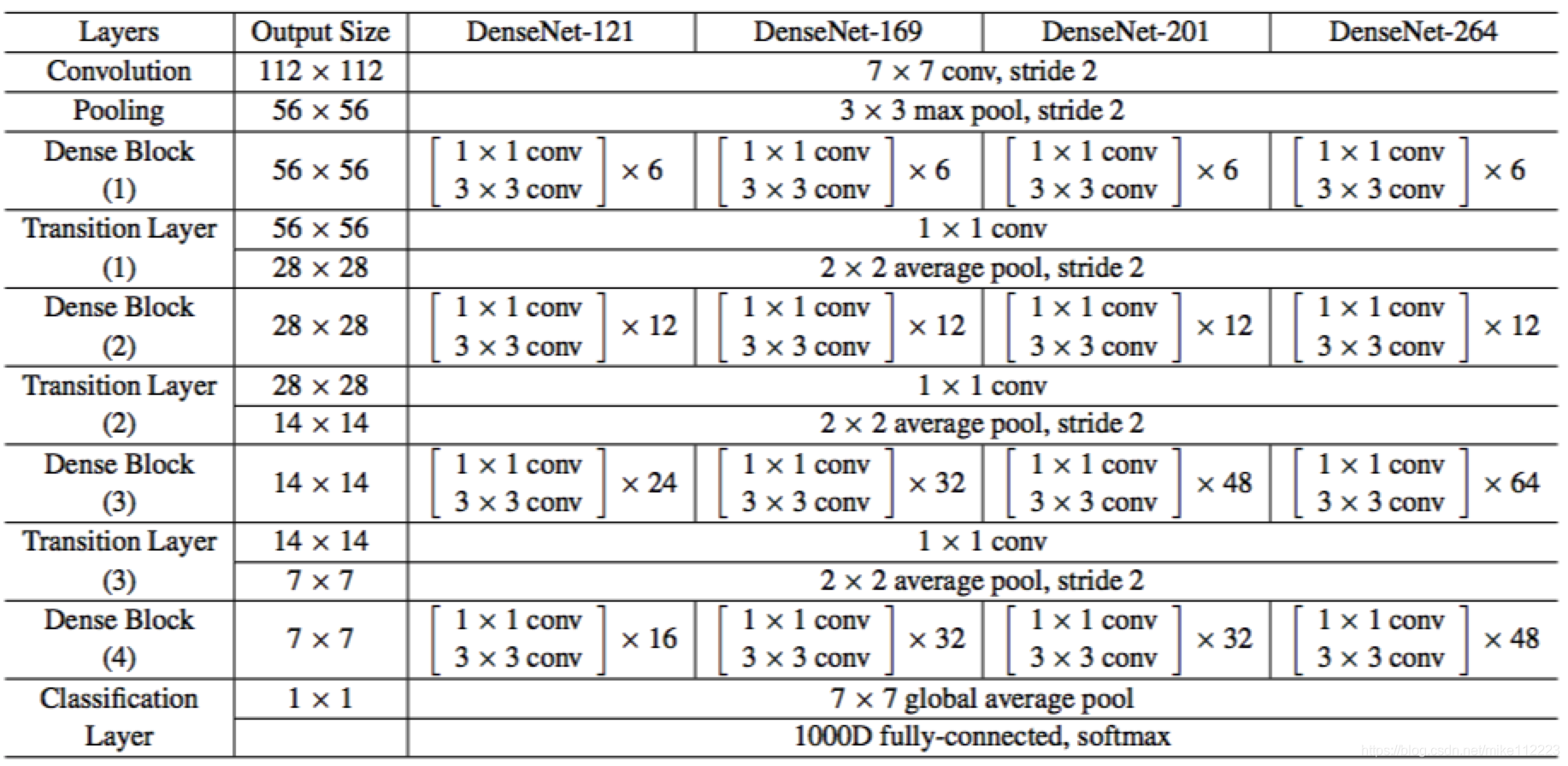
表1：DenseNet结构 for ImageNet。growth rate为k=32，这里conv表示BN-ReLU-Conv

5.Discussion

Model compactness. 因为直接将输入序列拼接起来，所以任意一层学习到的特征都是要优于前面层的。整个网络的特征复用使得整个网络更加紧凑。
通过实验也证明了，DenseNet的参数效用是更高的，优于ResNet。

Implicit Deep Supervision. 一种关于DenseNet能够取得更好的准确率的解释是，每个独立层都通过更短连接受到损失函数额外的监督（直观上理解就是每个独立层有多个输出了，那么自然反向传播的时候，就会有更多条路的梯度回传，也就是额外的监督）。我们可以称DenseNet在实行一种“深层监督”。这种深层监督的优势在之前的DSN中有所介绍。

Stochastic vs. deterministic connection. DenseNet和带随机深度归一化的ResNet有着很有趣的联系。在随机深度中，ResNet的层是被随机drop掉的，这就会使得相邻层可能会直接相连。因为池化层是不会被drop的，所以最后网络就会和DenseNet很相似。尽管方法论上是完全不同的，DenseNet也为随机深度这一成功的正则化提供了可能的解释。

Feature Reuse.

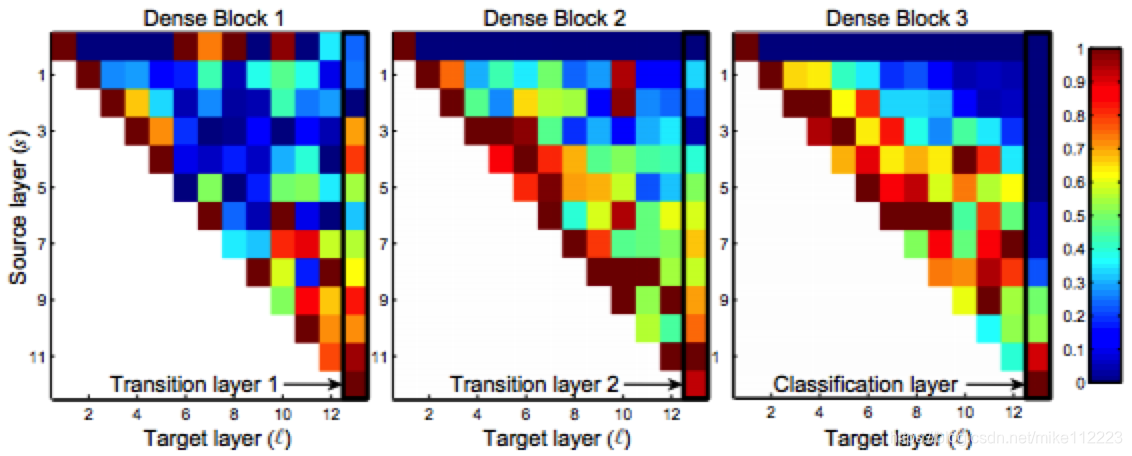
图5：经过训练的DenseNet上，卷积层的卷积核的权重的绝对平均值。像素$(s,l)$的颜色编码了一个Dense模块中连接$s$层到$l$层的权重的平均L1norm。三列被黑线框起来的部分分别表示两个过渡层和一个分类层。第一行编码了Dense模块中连接输入层的权重。

我们进行了实验来探究，训练过的网络是否充分利用了所有前面层的特征。图5展示了是三个dense模块的热点图。我们使用权重的平均绝对值来表征卷积层对于前面层的依赖情况。$(l,s)$上的红点表示$l$层充分利用了前面$s$层的特征。从图中我们观察到：

1. 在同一个模块中，所有层都通过多输入分散了它们的权重。这意味这很前面的层得到的特征也被深层使用。
2. 过渡层的权重同样分散到了之前dense模块的所有层，表明从整个网络的第一层到最后一层信息流基本都是直接传递的。
3. 第二和第三个dense模块都给过渡层的输出分配了最低的权重，这表明过渡层的输出带有很多冗余的特征。这与DenseNet-BC（输出被压缩）的结果相呼应。
4. 尽管最后分类层，也是使用了整个模块的权重，但是还是更倾向于集中最后的特征图，这表明网络深层得到了更多高级特征。

6.Conclusion.

DenseNet能扩展到百层，并且没有优化困难。在我们的实验中，随着参数的增加，DenseNet能够持续得到提升，并没有出现网络退化和过拟合。DenseNet可以在更少的参数和计算量的情况下，取得state-of-art的结果。关于DenseNet的参数配置我们是为了适配ResNet，所以后续如果仔细的调整参数和优化策略，预计会取得更好的结果。
仅仅是应用了一个简单的连接法则，DenseNet很自然的整合了恒等映射，深度监督和多样深度的特性。允许了整个网络的特征复用，使得学习更加紧凑。