红黑树的定义性质和插入删除

红黑树的定义与性质
定义：
红黑树是二叉排序树，需满足二叉排序树的性质，即左子树节点值≤根节点值≤右子树节点值，但与普通的二叉排序树相比，红黑树还需要满足以下几个特性：
1.每个节点非黑即红。
2.根节点必须是黑色。
3.叶子节点都是黑色的。（其中，叶子节点并不是树中的意思，而是指空节点、外部节点）
4.不存在两个相邻的红节点，对于红节点来说，它的父节点和子节点都为黑。
5.对于每一个节点，从该节点到任意一个叶子节点的简单路径上，所含的黑节点数目相同。
口诀：左根右，根叶黑，不红红，黑路同。

性质：
1.从根节点到叶节点的最长路径不大于最短路径的2倍

证明：最长路径即红黑交替，最短路径即路径上都为黑节点，根据不红红的定义，可证该性质
2.有n个内部节点的红黑树高度h ≤ 2log2(n+1)

在证明之前先引入一个概念：节点的黑高：从某节点出发，不含该节点，到达任意空叶节点的路径上黑节点的总数

证明：设一个红黑树的根节点的黑高为h，其内部节点最少的情况为一颗h层黑节点的满树(满树满足黑路同的定理)，所以内部节点最少为2^h-1
若红黑树高度为h，则该树根节点的黑高≥h/2(不红红的原理)，所以节点数n≥2^(h/2)-1，所以h≤2log2(n+1)

红黑树的插入(主要违背不红红的原则)
1.先查找，确定插入位置，插入新节点(左根右的原则进行查找)
2.若新节点是根，则染为黑色；若新节点非根，则染为红色(满足黑路同原则)
3.插入后，若满足那四个原则，结束
4.若不满足，进行调整，直到满足为止

调整方法：
看叔叔节点的颜色：
1.若为黑色：旋转+变色
LL型：右旋，父节点与爷节点交换，父节点与爷节点变色
RR型：左旋，与上面操作一致
LR型：先左旋，父节点与儿节点交换，再右旋，儿节点与爷节点交换，儿节点与爷节点变色
RL型：先右旋，父节点与儿节点交换，再左旋，儿节点与爷节点交换，儿节点与爷节点变色
2.若为红色：变色+变新
叔节点，父节点，爷节点都变色，将爷节点视为新节点，再进行判断

链接: 视频讲解

红黑树的删除(主要违背黑路同的原则)
删除操作与平衡二叉树的删除操作大致一致：
1.删除节点为叶子节点：
若删除节点为红节点，直接删除；
若删除节点为黑节点，引入双黑节点的概念：所有经过该节点的路径都会少一个黑节点。该叶子节点删除后，变成双黑节点。
消除双黑节点的操作：
看兄弟节点的颜色：
(1).若为黑色:分为两种情况：

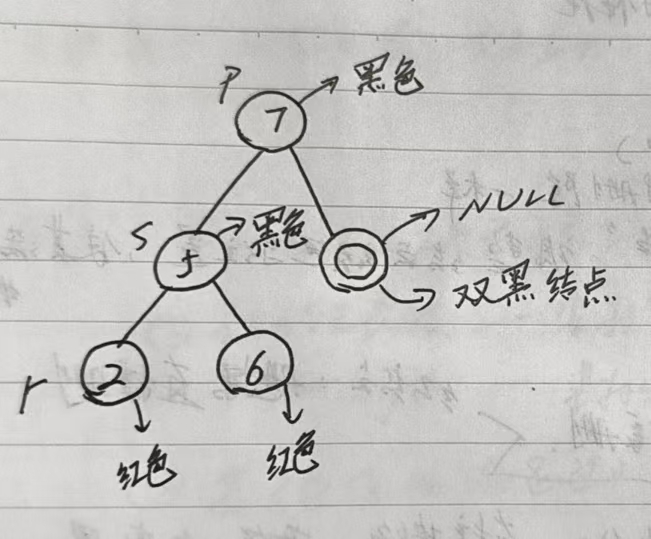
兄弟至少有一个红孩子：有四种情况：
LL型：s是p的左孩子，s的左孩子是红色：右旋，变色：r变为s，s变为p，p变为黑色
RR型：s是p的右孩子，s的右孩子是红色：左旋，变色在：与上述操作一致
LR型：先变色：r变为p，p变为黑色；再旋转：左旋p的左孩子，再右旋p
RL型：先变色：r变为p，p变为黑色；再旋转：右旋p的右孩子，再左旋p

兄弟孩子都为黑色：
兄弟节点变为红色，双黑节点上移，若遇到红色节点或根节点，双黑节点变为单黑节点，若没有，再走一遍上述的操作
(2).若为红色：
兄弟节点和父节点变色，二者朝双黑节点旋转，再继续调整
2.若删除节点有一个孩子节点：
子承父业，直接替换，然后变成黑色
其中只有一种情况父节点为黑色，子节点为红色，子节点要么在左，要么在右
3.若删除节点有两个孩子：
直接前驱或直接后继来代替，然后删除，最后转变为上述的两种情况
链接: 视频讲解