AVL--平衡二叉搜索树详图分析

于 2024-09-19 22:18:38 发布
阅读量1k 收藏 12
点赞数 26
文章标签： c++ 算法 数据结构 学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/microlovw/article/details/142362084
版权

二叉搜索树

一、AVL 树的定义与概述

在二叉搜索树中，左子树的所有节点的值都小于根节点的值，而右子树的所有节点的值都大于根节点的值。然而，普通的二叉搜索树在频繁的插入和删除操作后可能会变得高度不平衡，导致搜索、插入和删除操作的最坏情况时间复杂度退化为 O (n)，其中 n 是树中节点的数量。

AVL 树通过在每次插入或删除操作后自动调整树的结构来保持树的高度平衡，使得树的高度始终保持在 O (log n) 的范围内。这种平衡性质保证了 AVL 树的基本操作（如搜索、插入和删除）在最坏情况下的时间复杂度都是 O (log n)，从而提高了操作效率。

二、AVL 树的平衡因子

对于 AVL 树中的任何节点，其平衡因子只能是 - 1、0 或 1。当平衡因子为 0 时，表示该节点的左子树和右子树高度相等；当平衡因子为 1 时，表示左子树比右子树高 1；当平衡因子为 - 1 时，表示右子树比左子树高 1。如果在插入或删除操作后，某个节点的平衡因子超出了这个范围（即小于 - 1 或大于 1），则树的平衡被破坏，需要进行调整操作来恢复平衡

更新平衡因子情况

是否继续往上更新祖先，要看parent所在的子树高度是否变化

1、parent的平衡因子 == 0

说明更新前是1 or-1 一边高一边低，节点插入矮的那边

parent所在子树的高度不变，不需要继续往上更新

2、parent的平衡因子 == 1/-1

说明更新前是0，插入节点插入在任意一边

Parent子树高度都会变化了，需要继续往上更新

3、parent的平衡因子 == 2/-2

说明parent平衡因子更新前是 1/ -1

插入节点插入在了高的那边，

进一步加剧了parent所在子树的不平衡，已经违反规则了，需要旋转处理 

三、AVL 树的旋转操作

我们配合图片和代码看，更加易懂

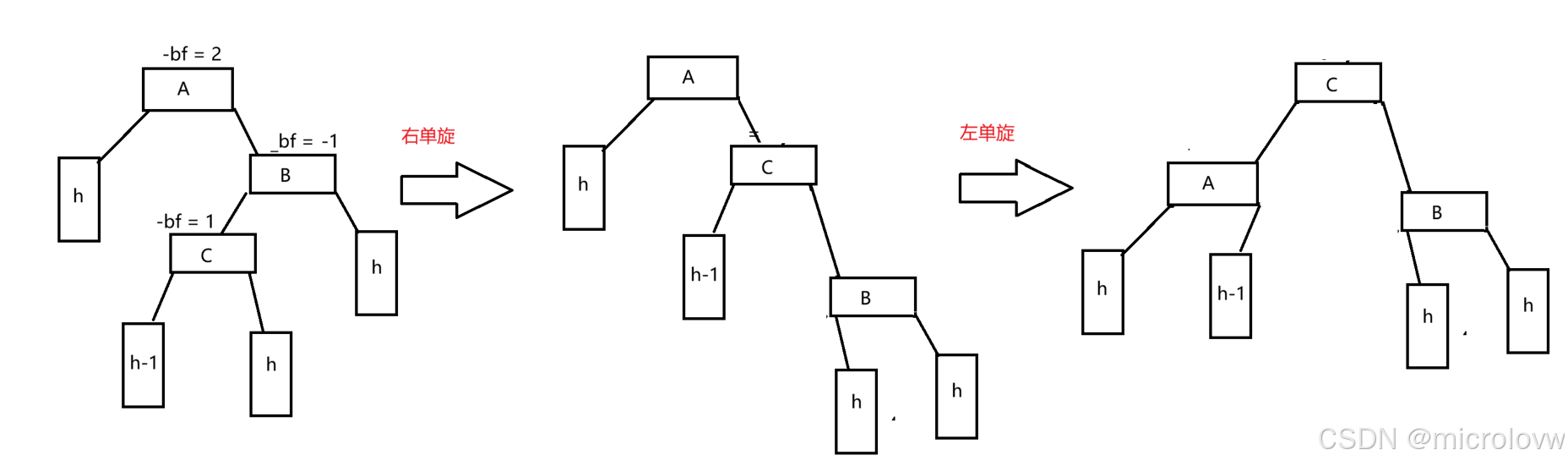
右单旋 

// 右单旋
void RotateR(Node* pParent)
{
    // 1. 确定相关节点
    Node* subL = pParent->_pLeft;
    Node* subLR = subL->_pRight;
    // 2. 进行节点连接的调整
    subL->_pRight = pParent;
    pParent->_pLeft = subLR;
    // 3. 处理父节点相关的连接
    Node* parentParent = pParent->_pParent;
    if (subLR)
        subLR->_pParent = pParent;
    subL->_pParent = parentParent;
    // 4. 根据原父节点的情况更新根节点或连接到合适的父节点
    if (parentParent)
    {
        if (pParent == parentParent->_pLeft)
        {
            parentParent->_pLeft = subL;
        }
        else if (pParent == parentParent->_pRight)
        {
            parentParent->_pRight = subL;
        }
    }
    else
    {
        _pRoot = subL;
    }
    // 5. 调整平衡因子
    subL->_bf = pParent->_bf = 0;
}

在这段代码中：

  • 首先，确定了参与旋转的关键节点，subL 是 pParent 的左子节点，subLR 是 subL 的右子节点。
  • 然后，通过调整节点之间的指针连接，将 subL 提升为新的父节点，pParent 变为 subL 的右子节点，subLR 成为 pParent 的左子节点。
  • 接着，处理了与父节点 parentParent 的连接关系。如果 parentParent 存在，根据 pParent 是其左子节点还是右子节点来正确连接 subL；如果 parentParent 不存在，说明 pParent 是根节点，此时更新 _pRoot 为 subL。
  • 最后，将 subL 和 pParent 的平衡因子都设置为 0，因为经过右单旋后这两个节点的子树高度差得到了调整，恢复到平衡状态。

左单旋

// 左单旋
void RotateL(Node* pParent)
{
    // 1. 确定相关节点
    Node* subR = pParent->_pRight;
    Node* subRL = subR->_pLeft;
    Node* parentParent = pParent->_pParent;
    // 2. 调整子节点与父节点之间的连接
    if (subRL)
        subRL->_pParent = pParent;
    pParent->_pRight = subRL;
    pParent->_pParent = subR;
    subR->_pLeft = pParent;
    subR->_pParent = parentParent;
    // 3. 根据原父节点的情况更新根节点或连接到合适的父节点
    if (parentParent)
    {
        if (pParent == parentParent->_pLeft)
            parentParent->_pLeft = subR;
        else
            parentParent->_pRight = subR;
    }
    else
    {
        _pRoot = subR;
    }
    // 4. 调整平衡因子
    subR->_bf = pParent->_bf = 0;
}

这里：

  • 首先明确了相关节点，subR 是 pParent 的右子节点，subRL 是 subR 的左子节点。
  • 之后，调整节点间的连接关系，将 subR 提升为新的父节点，pParent 变为 subR 的左子节点，subRL 成为 pParent 的右子节点，并处理好相关的父子节点连接关系。
  • 像右单旋一样，根据 parentParent 的情况更新根节点或正确连接新的子树结构。
  • 最后将 subR 和 pParent 的平衡因子都设为 0，表示经过左单旋后这两个节点的子树高度差恢复平衡

右左旋

// 右左双旋
void RotateRL(Node* pParent)
{
    Node* curRL = pParent->_pRight->_pLeft;
    Node* curR = pParent->_pRight;
    int judge = curRL->_bf;
    // 1. 先对右子树进行右单旋
    RotateR(pParent->_pRight);
    // 2. 再对整体进行左单旋
    RotateL(pParent);
    // 3. 根据中间节点curRL的平衡因子调整相关节点的平衡因子
    if (judge == 1)
    {
        pParent->_bf = -1;
        curR->_bf = 0;
    }
    else if (judge == -1)
    {
        pParent->_bf = 0;
        curR->_bf = 1;
    }
    else
    {
        return;
    }
}

在这个函数中：

  • 首先获取关键的中间节点 curRL，它是 pParent 的右子树的左子节点。
  • 先对 pParent 的右子树执行右单旋操作 RotateR(pParent->_pRight)，改变树的结构使其接近平衡。
  • 接着对整体执行左单旋操作 RotateL(pParent)。
  • 平衡因子为 1 的情况
    • 如果curLR - > _bf==1，这意味着在左旋之前，curLR的右子树相对较高。
    • 在左旋操作时，pParent - > _pLeft（设为curL）的平衡因子会变为 - 1，pParent的平衡因子变为 0。
    • 然后进行右旋操作，此时pParent的平衡因子变为 0，curL的平衡因子变为 - 1。
  • 平衡因子为 - 1 的情况
    • 当curLR - > _bf == - 1，说明在左旋之前，curLR的左子树相对较高。
    • 左旋操作后，curL的平衡因子变为 0，pParent的平衡因子变为 1。
    • 接着右旋操作，pParent的平衡因子变为 1，curL的平衡因子变为 0。
  • 平衡因子为 0 的情况
    • 若curLR - > _bf==0，表示curLR的左右子树高度相等。
    • 左旋操作后，curL的平衡因子变为 0，pParent的平衡因子也变为 0。
    • 由于已经达到平衡，不需要再对平衡因子进行特殊调整，所以在代码中直接返回

左右旋

// 左右双旋
void RotateLR(Node* pParent)
{
    Node* curLR = pParent->_pLeft->_pRight;
    Node* curL = pParent->_pLeft;
    int judge = curLR->_bf;
    // 1. 先对左子树进行左单旋
    RotateL(pParent->_pLeft);
    // 2. 再对整体进行右单旋
    RotateR(pParent);
    // 3. 根据中间节点curLR的平衡因子调整相关节点的平衡因子
    if (judge == -1)
    {
        pParent->_bf = 1;
        curL->_bf = 0;
    }
    else if (judge == 1)
    {
        pParent->_bf = 0;
        curL->_bf = -1;
    }
    else
    {
        return;
    }
}

代码中：

  • 先获取到关键的中间节点 curLR，它是 pParent 的左子树的右子节点。
  • 然后先对 pParent 的左子树执行左单旋操作 RotateL(pParent->_pLeft)，这一步将复杂的不平衡情况转化为相对简单的不平衡情况。
  • 接着对整体执行右单旋操作 RotateR(pParent)。
  • 平衡因子为 1 的情况
    • 当curRL - > _bf==1，意味着在右旋之前，curRL的右子树相对较高。
    • 右旋操作时，pParent - > _pRight（设为curR）的平衡因子变为 0，pParent的平衡因子变为 - 1。
    • 然后左旋操作，pParent的平衡因子变为 - 1，curR的平衡因子变为 0。
  • 平衡因子为 - 1 的情况
    • 如果curRL - > _bf == - 1，表示在右旋之前，curRL的左子树相对较高。
    • 右旋操作后，curR的平衡因子变为 1，pParent的平衡因子变为 0。
    • 接着左旋操作，pParent的平衡因子变为 0，curR的平衡因子变为 1。
  • 平衡因子为 0 的情况
    • 当curRL - > _bf==0，说明curRL的左右子树高度相等。
    • 右旋操作后，curR的平衡因子变为 0，pParent的平衡因子也变为 0。
    • 因为已经平衡，不需要进一步调整平衡因子，直接返回即可。

完整代码

功能只含插入，可以调试查看生产的AVL树是否正确

头文件

AVLTree.h

#pragma once
#include<iostream>
#include<assert.h>
using namespace std;

template<class T>
struct AVLTreeNode
{
	AVLTreeNode(const T& data = T())
		: _pLeft(nullptr)
		, _pRight(nullptr)
		, _pParent(nullptr)
		, _data(data)
		, _bf(0)
	{}

	AVLTreeNode<T>* _pLeft;
	AVLTreeNode<T>* _pRight;
	AVLTreeNode<T>* _pParent;
	T _data;
	int _bf;   // 节点的平衡因子
};


// AVL: 二叉搜索树 + 平衡因子的限制
template<class T>
class AVLTree
{
	typedef AVLTreeNode<T> Node;
public:
	AVLTree()
		: _pRoot(nullptr)
	{}

	// 在AVL树中插入值为data的节点
	bool Insert(const T& data)
	{
		Node* tmp = new Node(data);
		if (_pRoot == nullptr)
		{
			_pRoot = tmp;
			return true;
		}
		else
		{
			Node* cur = _pRoot;
			Node* curParent = _pRoot;
			while (cur)
			{
				if (cur->_data < data)
				{
					curParent = cur;
					cur = cur->_pRight;
				}
				else if (cur->_data > data)
				{
					curParent = cur;
					cur = cur->_pLeft;
				}
				else
				{
					return false;
				}
			}

			if (tmp->_data > curParent->_data)
			{
				curParent->_pRight = tmp;
			}
			else
			{
				curParent->_pLeft = tmp;
			}
			tmp->_pParent = curParent;
			cur = tmp;
			while (curParent)
			{
				if (cur == curParent->_pRight)
				{
					curParent->_bf++;
				}
				else
				{
					curParent->_bf--;
				}
				if (curParent->_bf == 0)
					return true;
				if (curParent->_bf > 1 && cur->_bf == 1)
				{
					RotateL(curParent);
					return true;
				}
				else if (curParent->_bf < -1 && cur->_bf == -1)
				{
					RotateR(curParent);
					return true;
				}
				else if (curParent->_bf < -1 && cur->_bf == 1)
				{
					RotateLR(curParent);
					return true;
				}
				else if (curParent->_bf > 1 && cur->_bf == -1)
				{
					RotateRL(curParent);
					return true;
				}
				else
				{
					cur = curParent;
					curParent = curParent->_pParent;
				}
			}
			return true;
		}

	}
	// AVL树的验证
	bool IsAVLTree()
	{
		return _IsAVLTree(_pRoot);
	}

private:
	// 根据AVL树的概念验证pRoot是否为有效的AVL树
	bool _IsAVLTree(Node* pRoot)
	{
		if (pRoot == nullptr)
			return true;

		int leftTreeHight = _Height(pRoot->_pLeft);
		int rightTreeHight = _Height(pRoot->_pRight);
		int level = rightTreeHight - leftTreeHight;

		if (level != pRoot->_bf || level > 1 || level < -1)
			return false;
		return _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight);
	}
	size_t _Height(Node* pRoot)
	{
		if (pRoot == nullptr)
			return 0;
		return 1 +max(_Height(pRoot->_pLeft) ,_Height(pRoot->_pRight));
	}
	// 右单旋
	void RotateR(Node* pParent)
	{
		Node* subL = pParent->_pLeft;
		Node* subLR = subL->_pRight;
		subL->_pRight = pParent;
		pParent->_pLeft = subLR;

		Node* parentParent = pParent->_pParent;
		if (subLR)
			subLR->_pParent = pParent;
		subL->_pParent = parentParent;

		if (parentParent)
		{
			if (pParent == parentParent->_pLeft)
			{
				parentParent->_pLeft = subL;
			}
			else if (pParent == parentParent->_pRight)
			{
				parentParent->_pRight = subL;
			}
		}
		else
		{
			_pRoot = subL;
		}
		subL->_bf = pParent->_bf = 0;

	}
	// 左单旋
	void RotateL(Node* pParent)
	{
		Node* subR = pParent->_pRight;
		Node* subRL = subR->_pLeft;
		Node* parentParent = pParent->_pParent;
		if (subRL)
			subRL->_pParent = pParent;
		pParent->_pRight = subRL;
		pParent->_pParent = subR;
		subR->_pLeft = pParent;
		subR->_pParent = parentParent;
		if (parentParent)
		{
			if (pParent == parentParent->_pLeft)
				parentParent->_pLeft = subR;
			else
				parentParent->_pRight = subR;
		}
		else
		{
			_pRoot = subR;
		}
		subR->_bf = pParent->_bf = 0;
		
	}
	// 右左双旋
	void RotateRL(Node* pParent)
	{
		Node* curRL = pParent->_pRight->_pLeft;
		Node* curR = pParent->_pRight;
		int judge = curRL->_bf;
 		RotateR(pParent->_pRight);
		RotateL(pParent);
		if (judge == 1)
		{
			pParent->_bf = -1;
			curR->_bf = 0;
		}
		else if (judge == -1)
		{
			pParent->_bf = 0;
			curR->_bf = 1;
		}
		else
		{
			return;
		}
	}
	// 左右双旋
	void RotateLR(Node* pParent)
	{
		Node* curLR = pParent->_pLeft->_pRight;
		Node* curL = pParent->_pLeft;
		int judge = curLR->_bf;
		RotateL(pParent->_pLeft);
		RotateR(pParent);
		if (judge == -1)
		{
			pParent->_bf = 1;
			curL->_bf = 0;
		}
		else if (judge == 1)
		{
			pParent->_bf = 0;
			curL->_bf = -1;
		}
		else
		{
			return;
		}
	}

private:
	Node* _pRoot;
};


void testTree()
{
	//16, 3, 7, 11, 9, 26, 18, 14, 15
	AVLTree<int> T;
	T.Insert(4);
	T.Insert(2);
	T.Insert(6);
	T.Insert(1);
	T.Insert(3);
	T.Insert(5);
	T.Insert(15);
	T.Insert(7);
	T.Insert(16);
	T.Insert(14);

}

源文件

TestAVLTree.cpp

#include"AVLTree.h"

int main()
{
	testTree();
	return 0;
}

microlovw
关注
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值