C++学习日记（变量）

变量的生存范围：一个变量从声明到结束的过程

局部作用域

在函数体内或复合语句内部定义的一个变量（包括main函数）

局部变量未初始化时其值是随机的

程序执行到函数体或复合语句之外时这个变量就会自动释放

全局作用域

变量、常量等对象的作用范围为整个程序

全局变量的生命期始于程序的运行，结束于程序的退出

全局变量未初始化时其值为0

如果程序中存在同名的全局变量和局部变量，采用就近原则引用

静态存储变量

静态存储变量的值在调用结束后并不释放空间而是一直保留原值，下次调用时该变量值是上一次调用结束后的已有的保存值

static <变量类型><变量名称>;

//静态存储变量的使用
#include<iostream>
using namespace std;
void f1(int, int);
int main()
{
    int i = 5, j = 10, k;
    for (k = 1; k <= 3; k++)
    {
        f1(i, j);
    }
    cin.get();
    return 0;
}
void f1(int a, int b)
{
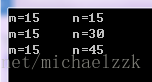
    int m = 0;  //定义自动变量m
    static int n = 0; //定义静态变量n
    m = m + a + b; //使用自动变量m求和
    n = n + a + b;//使用静态变量n求和
    cout << "m=" << m << '\t' << "n=" << n << endl;
}