AVL树（C语言实现）

原创

已于 2022-02-10 17:00:05 修改 · 2.8k 阅读

34 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #avl

于 2022-02-09 00:55:54 首次发布

本文详细介绍了AVL树的原理和C语言实现，包括节点定义、高度计算、失衡节点查找与调整、插入、删除操作。通过层次遍历寻找失衡节点并进行四种类型的旋转调整，确保树保持平衡。同时，提供了完整的C代码实现AVL树的创建、插入和删除功能，以及删除节点后的平衡调整。

AVL树（C语言实现）

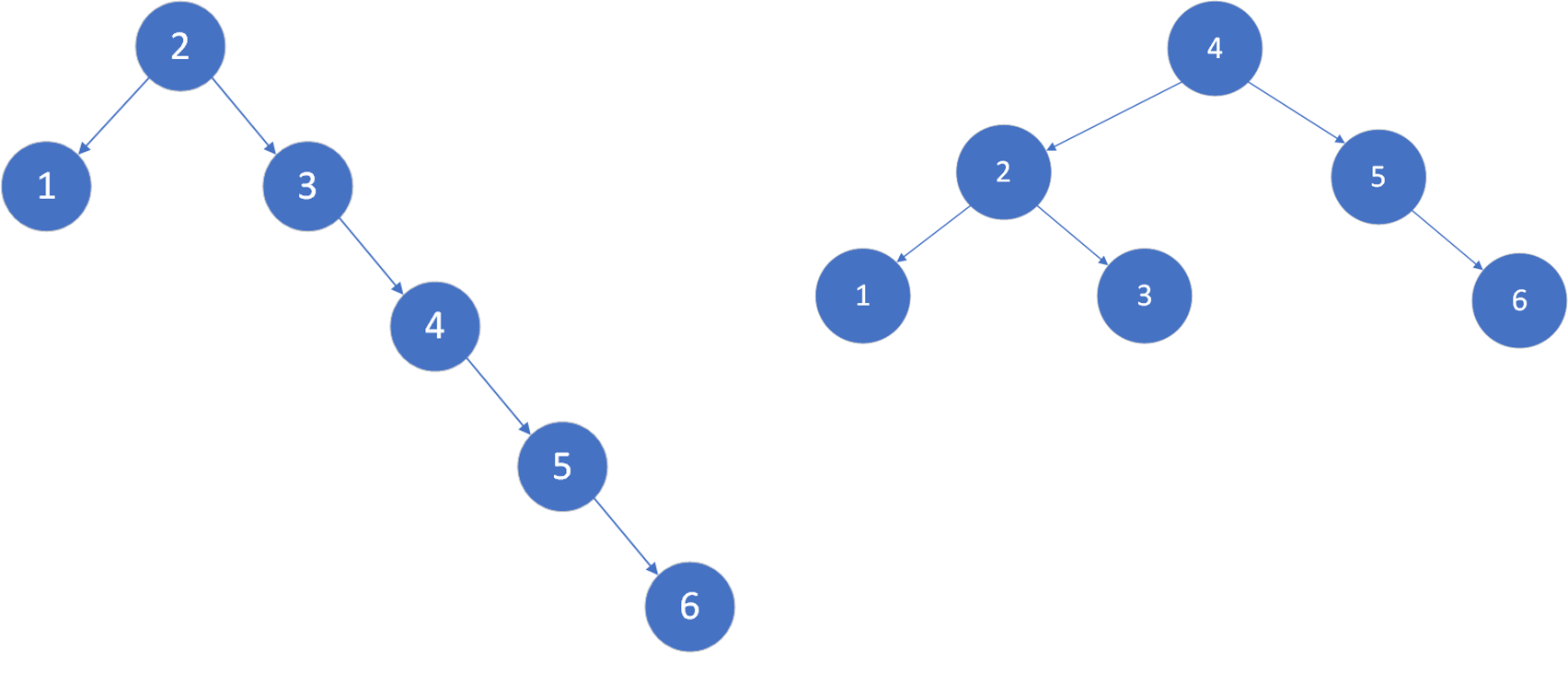
插入、删除和查找是树的几种基本操作。对于插入或删除这个动作而言，其所花时间为常数时间，整个操作的大部分时间在于找到要插入或删除的节点所花的时间。树的高度越大，查找所花的时间也就越大，为减小对树进行操作所花的时间，我们总希望树越矮越好。对于同样的一组集合，左边的树更像一个链表，其平均查找次数大于右边的树。

组合1.png

失衡情况

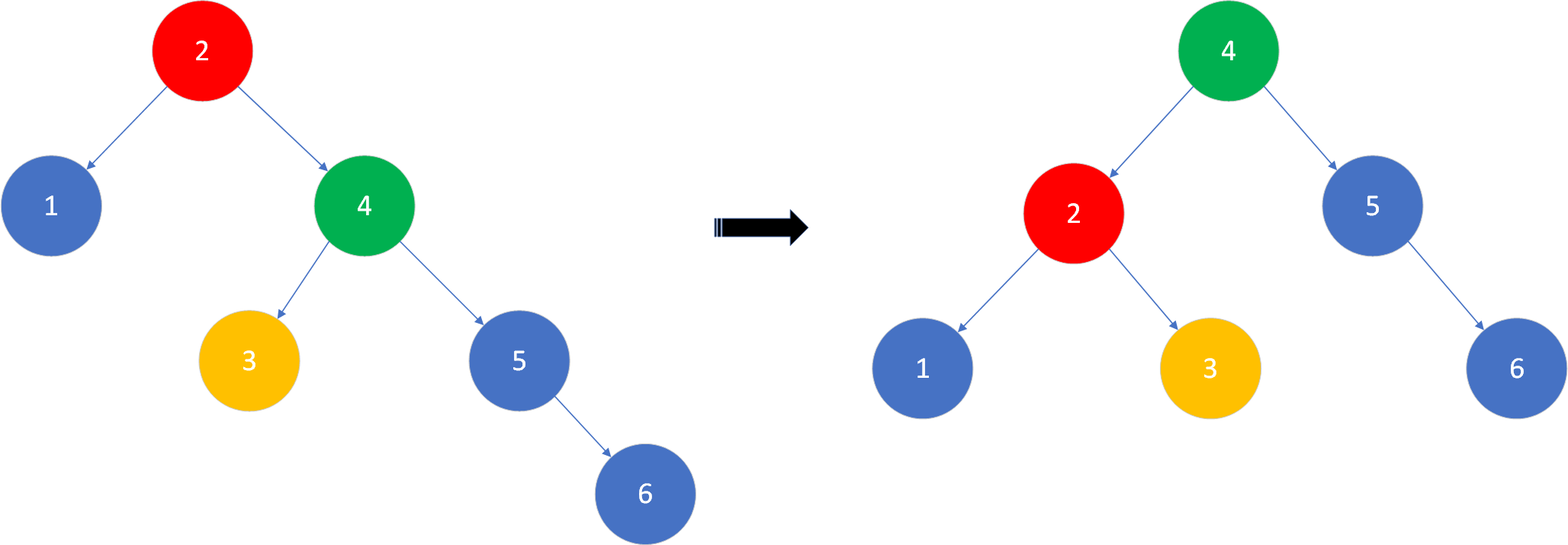
L-L型失衡：失衡节点的平衡因子大于1，失衡发生在失衡节点的左孩子的左子树上。表现为：左孩子的高度大于右孩子的高度，左孩子的左子树的高度大于其右子树的高度。为使树平衡，应对失衡节点进行右旋操作（顺时针旋转），失衡节点的左孩子更新为失衡节点左孩子的右子树，失衡节点的原左子树的右孩子更新为失衡节点，新的根节点为失衡节点的原左孩子。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CaGUDU1q-1644339259920)(https://s2.loli.net/2022/01/21/TAVasdO1UmGbpkE.png)]
R-R型失衡：失衡节点的平衡因子小于-1，失衡发生在失衡节点的右孩子的的右子树上。表现为：右孩子的高度大于左孩子的高度，右孩子的右子树的高度大于其左子树的高度。为使树平衡，对失衡节点进行左旋操作（顺时针旋转），操作与L-L型的调整操作类似。
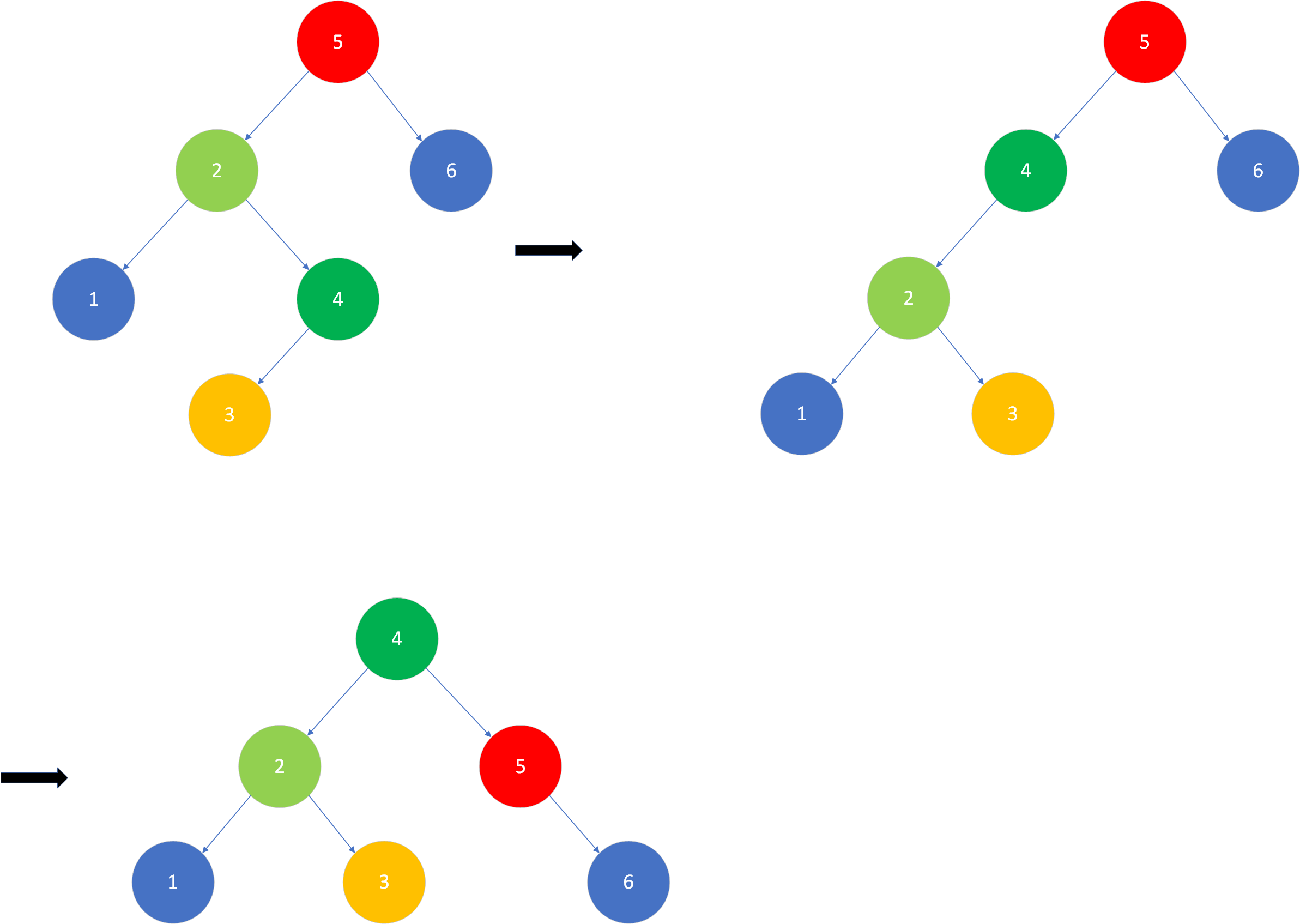
L-R型失衡：失衡节点的平衡因子大于1，失衡发生在失衡节点的左孩子的右子树上，注意和失衡节点的左孩子的右子树的左右子树无关，下边的R-L型失衡同理。表现为：左孩子的高度大于右孩子的高度，且左孩子的右子树的高度大于左孩子左子树的高度。首先对失衡节点的左孩子进行左旋操作（逆时针旋转），再对失衡节点进行右旋操作（顺时针旋转）。可以发现，L-R失衡的调整操作是R-R型调整和L-L型失衡调整的组合，R-L型失衡的调整也是同一个道理。
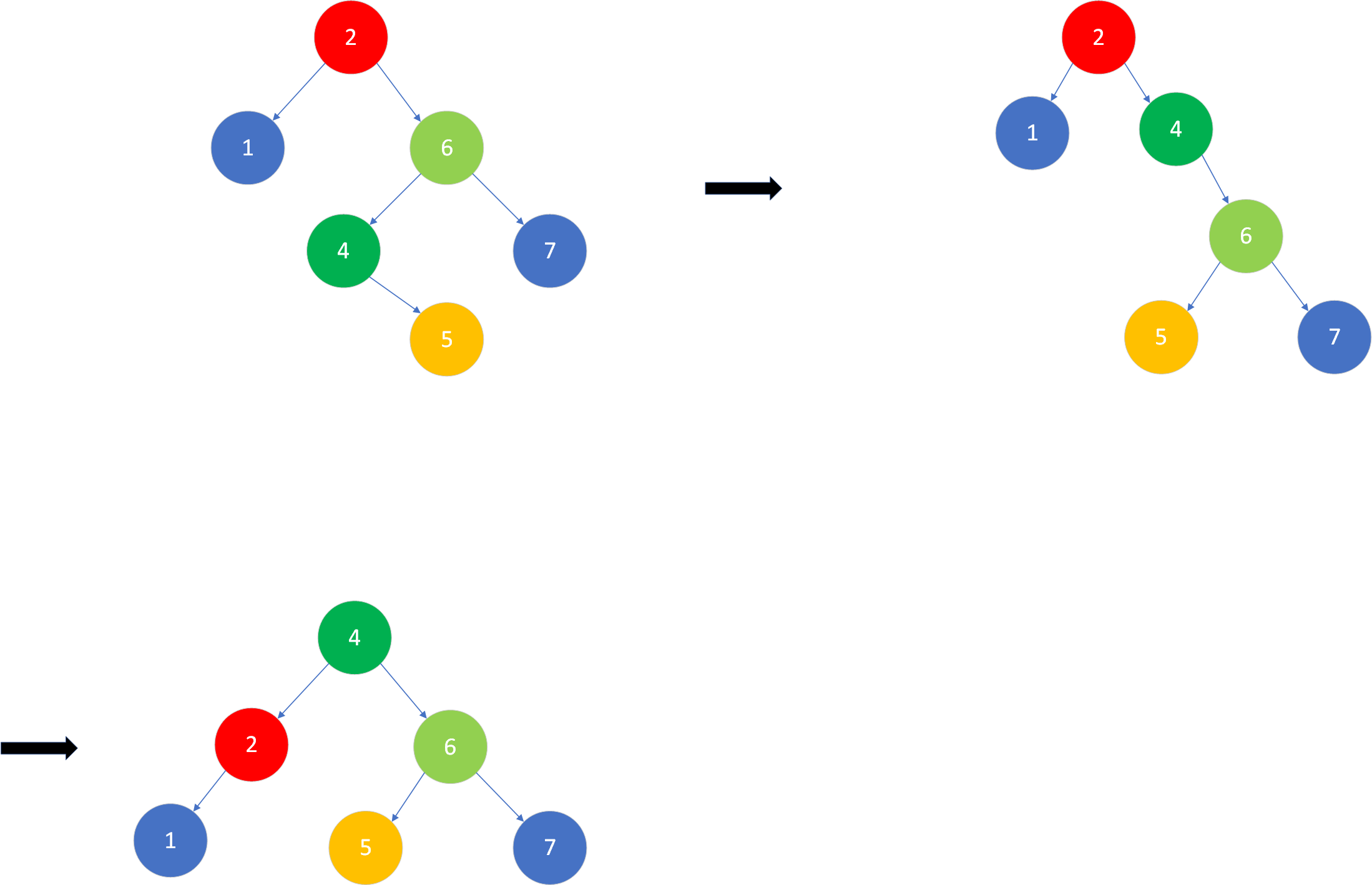
R-L型失衡：失衡节点的平衡因子小于-1，失衡发生在失衡节点的右孩子的左子树上。表现为：失衡节点的右孩子的高度大于左孩子的高度，且右孩子的左子树高度大于右子树的高度。首先对失衡节点的右孩子进行右旋操作（顺时针旋转），再对失衡节点进行左旋操作（逆时针旋转）。

建树思路

从空树开始，直接插入一个节点；对于非空的树，找到插入位置（若插入的元素已存在则不用操作），插入节点，检查树中是否有失衡节点，若有，则进行调整。建树思路清晰简单，但实现起来需要考虑许多细节。情况是否考虑周全，语言的特性都在考虑的范围内。

C代码实现

节点的定义

struct TreeNode{
     
     
    struct TreeNode *left;
    struct TreeNode *right;
    struct TreeNode *parent;
    ElementType element;
};
typedef struct TreeNode Node;

节点的高度

int GetHeight(Node *node)
{
     
     
    if ( node == NULL )
        return -1;

    int leftchildheight = GetHeight(node->left);
    int rightchildheight = GetHeight(node->right);
    return ( leftchildheight > rightchildheight ? leftchildheight: rightchildheight) + 1;
}

找到插入的位置（节点）

Node *FindNodeToBeInserted(ElementType element, Node *root)
{
     
     
    Node *tmp = root;
    Node *parent = NULL;

    while ( tmp != NULL )
    {
     
     
        if ( element < tmp->element )
        {
     
     
            parent = tmp;
            tmp = tmp->left;