解题报告 之 HDU5334 Virtual Participation
Description
As we know, Rikka is poor at math. Yuta is worrying about this situation, so he asks rikka to have some practice on codeforces. Then she opens the problem B:
Given an integer , she needs to come up with an sequence of integers
, she needs to come up with an sequence of integers
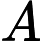 satisfying that the number of different continuous subsequence of
satisfying that the number of different continuous subsequence of
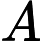 is equal to
is equal to
 .
.
Two continuous subsequences


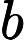 are different if and only if one of the following conditions is satisfied:
are different if and only if one of the following conditions is satisfied:
1. The length of is not equal to the length of
is not equal to the length of
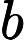 .
.
2. There is at least one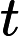 that
that


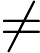
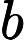
 , where
, where

 means the
means the
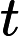 -th element of
-th element of
 and
and
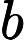
 means the
means the
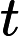 -th element of
-th element of
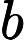 .
.
Unfortunately, it is too difficult for Rikka. Can you help her?
Given an integer
 , she needs to come up with an sequence of integers
, she needs to come up with an sequence of integers
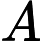 satisfying that the number of different continuous subsequence of
satisfying that the number of different continuous subsequence of
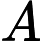 is equal to
is equal to
 .
.
Two continuous subsequences



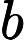 are different if and only if one of the following conditions is satisfied:
are different if and only if one of the following conditions is satisfied:
1. The length of
 is not equal to the length of
is not equal to the length of
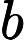 .
.
2. There is at least one
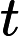 that
that


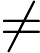
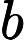
 , where
, where

 means the
means the
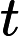 -th element of
-th element of
 and
and
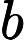
 means the
means the
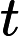 -th element of
-th element of
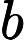 .
.
Unfortunately, it is too difficult for Rikka. Can you help her?
Input
There are at most 20 testcases,each testcase only contains a single integer









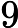










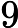

Output
For each testcase print two lines.
The first line contains one integers





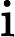
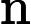







 .
.
The second line contains space-separated integer
space-separated integer
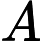





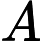



 - the sequence you find.
- the sequence you find.
The first line contains one integers






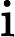
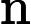







 .
.
The second line contains
 space-separated integer
space-separated integer
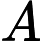





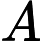



 - the sequence you find.
- the sequence you find.
Sample Input
10
Sample Output
4
1 2 3 4
题目大意:要求你构造一个数字序列,这个序列中不相同的连续子序列数为K。这些连续子序列不相同要么长度不同,或者长度相同但存在一个位置的数字不相同。输出找到的序列有多少个数构成,再输出这些数。(要求构造的序列长度不超过1e5)
分析:一开始没什么思路,后来看了题解才知道的。首先明确,如果这个序列由一种数构成(如仅由1构成),长度为a。那么子序列数量为a个;如果由1111122222……构成,其中1长度为a,2长度为b,那么子序列数量为a+b+a*b(选几个1选几个2);如果由11111222223333……构成,那么子序列数量为a+b+c+a*b+b*c+a*c,分别对应只选1,只选2,只选3,选几个1几个2,选几个2几个3,选几个1而2全选再选几个3。
第一种情况,K<=1e5,那么直接输出K个1即可。
第二种情况,K>1e5,用1、2、3可以构造(这里我也不知道为什么?求大神解答)。那么假设有a个1,b个2,c个3。
那么就是要求a+b+c+a*b+b*c+a*c=K的解。化简一下得到(a+c+1)*(b+c+1)= K+c^2+c+1;
然后枚举c,K为已知数,然后枚举右边的约数(这也是化简的原因),看满不满足(a+c+1)、(b+c+1)都合法。如果找到合法,就反解出abc然后输出完事。
另附官方做法,更加是看不懂,数学渣渣表示跪了。(http://blog.youkuaiyun.com/u010660276/article/details/47188023)
上代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
typedef long long ll;
int main()
{
ll k;
while(cin >> k)
{
if(k <= 1e5)
{
cout <<k << endl;
for(int i = 1; i <= k; i++)
{
printf( "1" );
if(i == k) printf( "\n" );
else printf( " " );
}
continue;
}
ll a, b, c=0;
int flag = 0;
while(1)
{
ll s = k + c*c + c + 1;
for(int i = c + 1; i*i <= s; i++)
{
a = i;
if(s%a != 0)continue;
b = s / a;
if(b < c + 1)continue;
if(a + b - c - 2 <= 1e5)
{
flag = 1;
break;
}
}
if(flag) break;
else c++;
}
cout << a + b - c - 2 << endl;
for(int i = 1; i <= a - c - 1; i++)
printf( "1 " );
for(int i = 1; i < b - c - 1; i++)
printf( "2 " );
if(c == 0) printf( "2\n" );
else
{
printf( "2 " );
for(int i = 1; i < c; i++)
printf( "3 " );
printf( "3\n" );
}
}
return 0;
}





 本文深入解析HDU5334 Virtual Participation问题的解题思路,通过输入输出规范详细阐述了如何构造满足条件的序列,并提供了两种不同情况下的解题方法。此外,还附上了官方做法的解读,帮助读者更好地理解问题本质及算法应用。
本文深入解析HDU5334 Virtual Participation问题的解题思路,通过输入输出规范详细阐述了如何构造满足条件的序列,并提供了两种不同情况下的解题方法。此外,还附上了官方做法的解读,帮助读者更好地理解问题本质及算法应用。
















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








