趣题：等腰直角三角形与勾股定理形式的条件

    
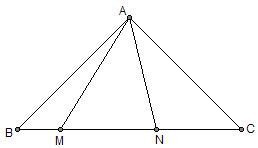
    等腰直角三角形ABC，斜边BC上有两点M、N 满足BM^2 + NC^2 = MN^2。求证：∠MAN为45度。这个图形最早出现在2001年罗马尼亚数学奥赛的一道题目中。
    看答案前我先说点别的事……有多少网友住在北京？这次清北还在那个地方么？假期我没事干，想和大家一起聚一聚，吃个饭，喝个夜啤酒什么的……不知道为什么，最近酒瘾特别大。
    答案在下面。







































    
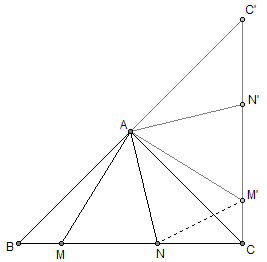
    证明：将整个图形绕A点逆时针旋转90度。显然∠MAM'为90度，BCC'也为90度。连接M'N，则BM^2 + NC^2 = M'C^2 + NC^2 = M'N^2，于是MN = M'N。又AM = AM', AN = AN，由SSS可知△AMN≌△AM'N，这样∠MAN和∠M'AN都是45度。

来源：cut-the-knot新文
Matrix67原创翻译