Benjamin Franklin的另类幻方

    Benjamin Franklin是一个与Leonardo da Vinci同样神秘的人，他是一个伟大的物理学家、发明家、文学家、实业家、政治家、思想家、社会活动家。他一生中留下了许多的迷，电影National Treasure里提到的绝大多数关于Benjamin Franklin的事情都是真的。刚出版的一本名为Benjamin Franklin's Numbers: An Unsung Mathematical Odyssey的书中提到，人们还长期忽视了Benjamin Franklin的一些数学成就。Franklin曾计算过战争的经济开销，曾做过人口数预计，这都是没有先例的。其中，最有趣的数学创造还是要数Franklin的“另类幻方”。
    一个3x3的幻方是这样的一个九宫格，格子里写有1到9这9个数字，每一行、每一列和两条对角线上的三个数加起来都是一个相同的数。当然，更大一些的幻方也是存在的，例如你可以用前16个正整数排列成4x4的幻方。Franklin发明了一些另类的幻方，它的要求更加严格，但看上去似乎更有意思一些。Franklin在一封信中写道：“我不满足于这些普通的幻方，这都是很普遍、很简单的东西了。我给我自己强加了一些任务，然后成功地创造出了一些具有其它各种性质的幻方，它们看上去更加神奇。”Franklin创造了下面这个8x8的幻方，每种颜色的数字加起来都等于260，不同寻常的是，你有至少六种方法去解读它。
  

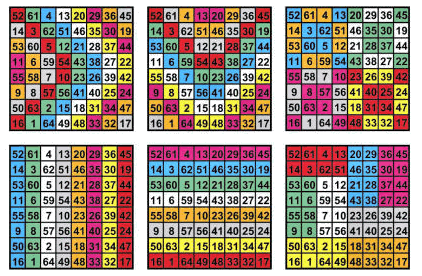
    更牛B的是Franklin的16x16幻方，他称它为“史上最神奇的幻方”。在这个幻方中，每一行、每一列和每一个“//”形区域内的数字和都是2056。更不可思议的是，每一个4x4的子正方形内的数字之和也是2056 ！
  

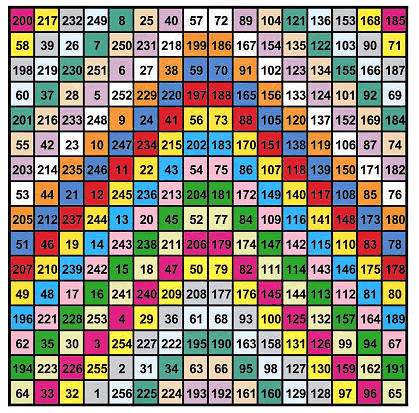
    Franklin仍不感到满足。Franklin想，既然有“幻方”，为什么没有“幻圆”？于是Franklin构造出了下面这个图形。这个图形里，每一条半径、每一个同心圆和图中画出的每一个偏心圆内的数字加起来都是360。
  

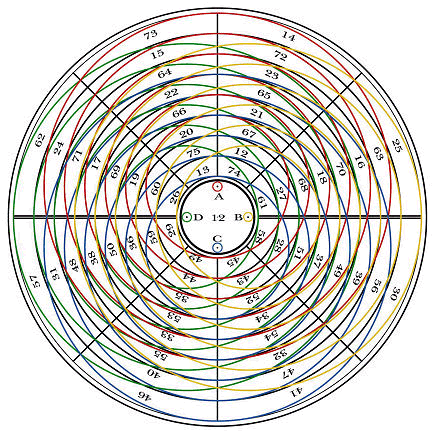
    你可以从下面这个图中看出上图的偏心圆是怎么画出来的。
  

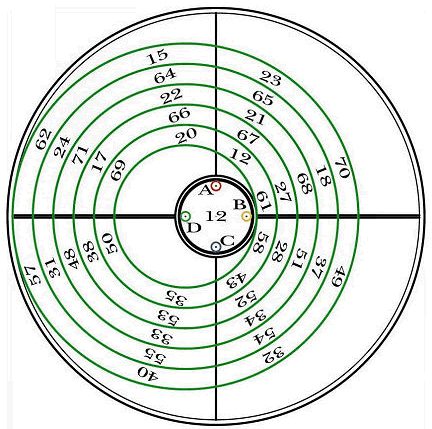
阅读更多：http://blog.sciencenews.org/mathtrek/2008/01/benjamin_franklin_plays_sudoku.html