63岁以色列数学家Avraham成功解决公路涂色问题

    以色列数学家Avraham Trakhtman最近解决了一个非常有名的数学难题——公路涂色问题(Road Coloring Problem)。这是图论中的一个著名猜想，最早由Benjamin Weiss和Roy Adler在1970年提出。63岁的Avraham用铅笔草草写下了仅仅8页的证明过程，出人意料地解决了这个问题。该问题的解决对道路规划等很多现实社会中的问题都有帮助。
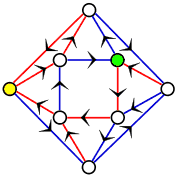
    给定一个有向图G（即图中的每一条边都单向地从某个顶点指向另一个顶点），其中每一个点的出度（向外走的边的条数）都为k。假设我们用k种颜色对图G中的所有边进行染色，使得每个点的k条出边的颜色都不相同，并且对于每一个顶点v，总存在一个颜色序列，使得不管你从哪里出发，按照这个颜色序列不断走下去，最终都能到达顶点v。我们称满足这些条件的涂色方案叫做一个同步着色(synchronizing coloring)。Benjamin Weiss和Roy Adler猜想，如果一个有向图是强连通的（任两点间都可互相到达）并且是非周期性的（所有环的长度的最大公约数为1），则该图一定存在同步着色方案。例如，右面这个图就是一个合法的同步着色方案，每个点的两条出边恰好一红一蓝。我们可以找几个点简单验证一下：不管你在哪里，按“蓝-红-红”走最终总会到那个黄色的点；类似地，不断按“蓝-蓝-红”走，不管出发点在哪里你最后总会走到绿色的点。

    这个猜想的完整证明过程可以在这篇论文里找到。论文只有几页，估计我应该能看懂，看懂了的话我会更新出来的。

查看更多：来源1  来源2