最近几天见到了几道零散的、不成系统的趣题,在这里合成一篇文章,与大家分享。
1. 证明:对任意正整数n,n^2+n+1一定不是完全平方数。
2. 说一个实数是可表达的,当且仅当它能用有限长的语句明确地描述出来,如2147483648可以说成是“二的三十一次方”,√2即为“平方后等于二的正实数”,π即为“圆的周长和直径之比”。问题是,是否存在一个不可表达的实数?
3. 一个人有两个小孩儿,其中有一个生于星期二的男孩儿。问另一个是男孩儿的概率是多少?
4. 无需积分,计算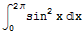 。
。
1. 证明:对任意正整数n,n^2+n+1一定不是完全平方数。
答案:n^2+n+1大于n^2而小于(n+1)^2,位于两个相邻平方数之间,显然不可能是一个完全平方数。
2. 说一个实数是可表达的,当且仅当它能用有限长的语句明确地描述出来,如2147483648可以说成是“二的三十一次方”,√2即为“平方后等于二的正实数”,π即为“圆的周长和直径之比”。问题是,是否存在一个不可表达的实数?
答案:存在。因为有限长的字符串是可数的(按字符串的长度排序,长度相同则按字典序排),但实数集是不可数的。有趣的是,这个问题的证明一定是非构造性的。
3. 一个人有两个小孩儿,其中有一个生于星期二的男孩儿。问另一个是男孩儿的概率是多少?
答案:13/27。这是“已知有一个男孩儿,问另一个是男孩儿的概率”的加强版,是一个非常精彩的条件概率问题。它非常直观地告诉我们,事先提供更准确的信息能给概率带来怎样的变化。另一个有趣的问题见这里。
4. 无需积分,计算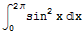 。
。
答案:显然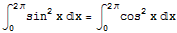 。但是,我们有
。但是,我们有
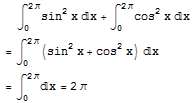
于是立即可知,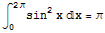 。
。























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








