服务器ILP实验的一些操作

原创已于 2022-07-02 13:38:11 修改 · 481 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#服务器 #linux

于 2022-07-02 11:22:21 首次发布

科研专栏收录该内容

4 篇文章

订阅专栏

本文介绍了常用的命令行操作，包括文件和文件夹的创建与删除、Python程序的执行与暂停、Anaconda环境的搭建与管理、后台进程的创建与管理等。适用于初学者快速掌握Linux环境下基本操作。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

- 常用命令行操作

常用命令行操作

命令行创建/删除文件夹/文件

创建文件夹

mkdir 文件夹名

创建文件

touch 文件名

删除文件夹

参考博客Linux终端删除文件夹命令：
感谢大佬！！
之前介绍过Linux系统删除文件命令，也就是 rm 命令，实际上rm命令也可以用于删除文件夹，而且比 rmdir 要方便非常多。

但是，使用 rm 命令删除文件夹的时候，一定要记得加上 -r 或 -R 选项，否则会报错。该选项表示递归删除文件夹，可以将该文件夹下的文件全部删除。加上 -f 选项将强制删除而不给任何提示。

# 删除目录不加 -r 会报错
$ rm data
rm: cannot remove ‘data’: Is a directory
# 正确删除目录
$ rm -r data
# 强制删除目录
$ rm -rf data

命令行执行python程序

文件名为exp3.py，则先进入程序所在文件下，命令为

python exp3.py

命令行暂停正在执行的python程序

crlt+c

使用Anaconda时，下载python程序中缺少的包

假设需要下载的包是pyrsistent

conda install pyrsistent

在服务器搭建Anaconda

参考博客在服务器上搭建自己的python环境(针对小白)
感谢大佬！！
进入这个网址：https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/?C=M&O=D
点这里，找到最新的适合linux服务器的。
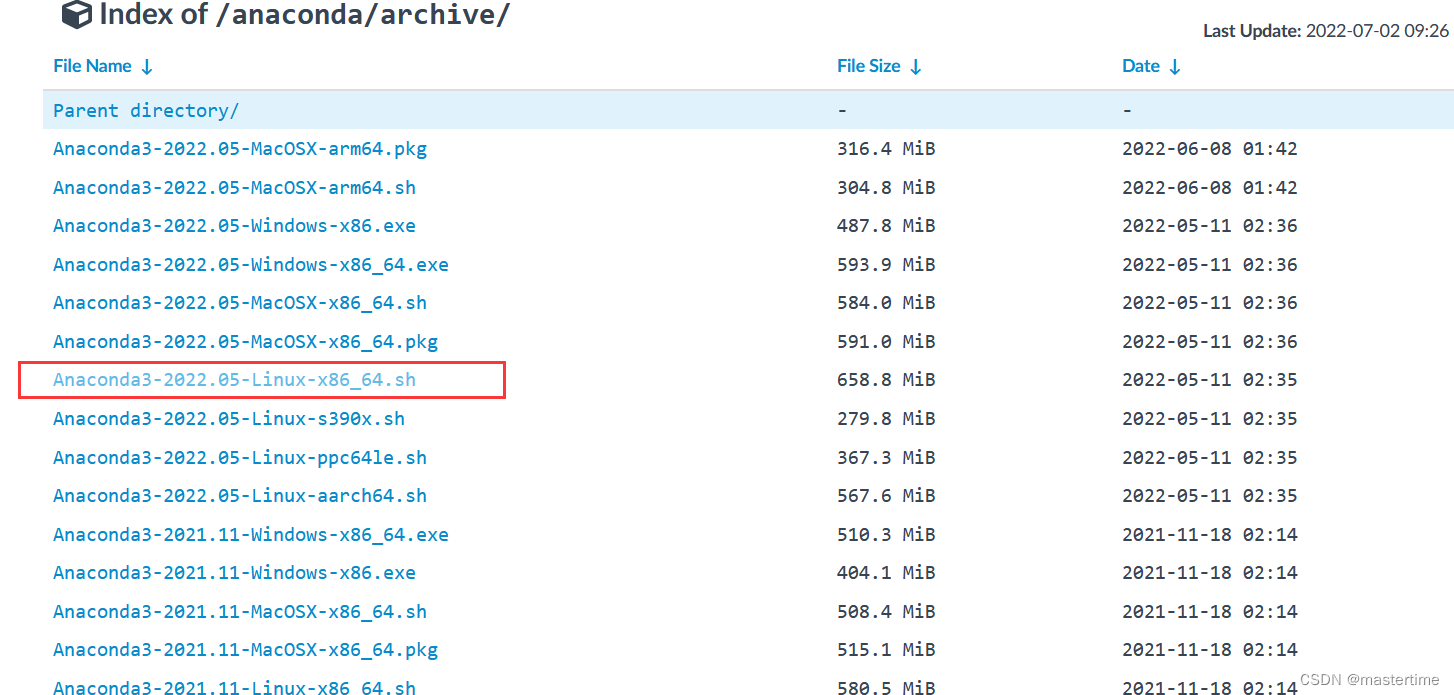选择合适的版本右键获取链接
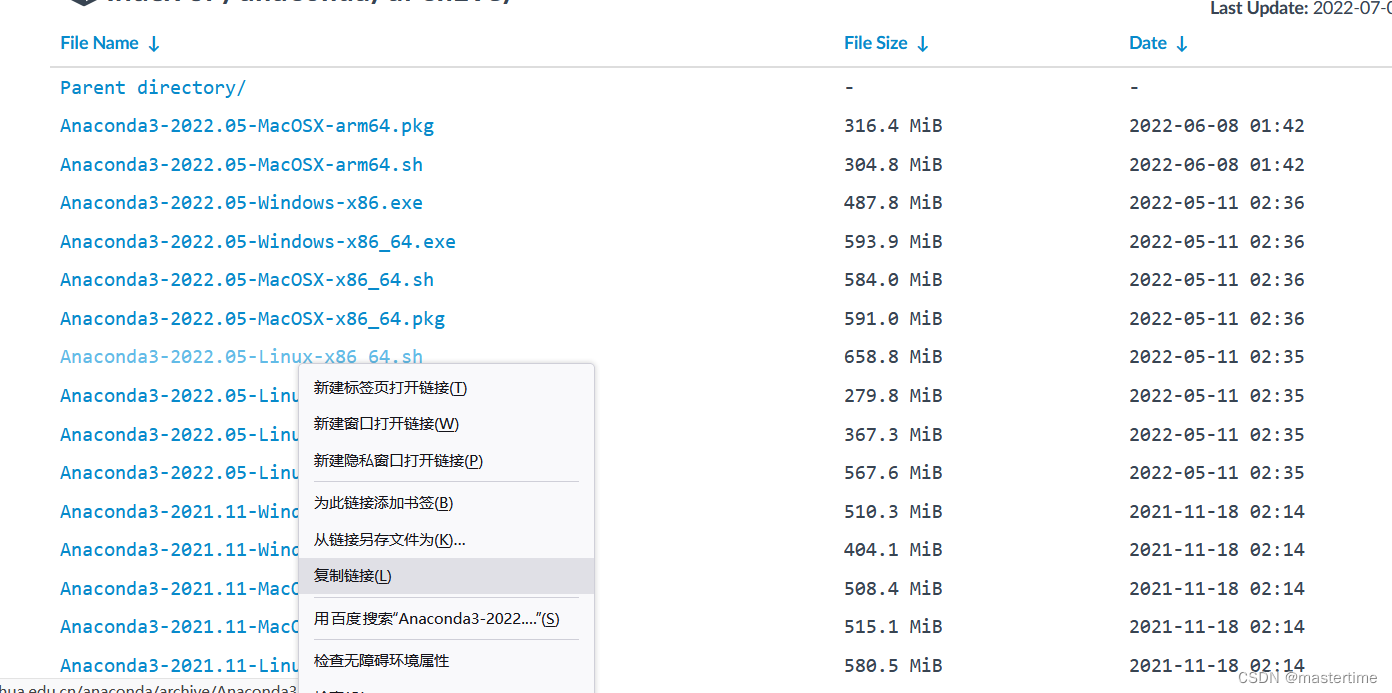在linux终端用wget命令下载anaconda

wget https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/Anaconda3-2022.05-Linux-x86_64.sh

下载完毕后，bash+下载的anaconda文件

bash Anaconda3-2022.05-Linux-x86_64.sh

之后不断回车，然后不断yes，直到结束
配置环境变量

source ~/.bashrc

创建虚拟环境，名为seg，指定python版本3.7

conda create -n seg python=3.7

启用自己的虚拟环境

seg为虚拟环境的名字

conda activate seg

若想返回base环境

deactivate

如果想查看目前有哪些环境可以输入

conda env list

想删除环境，则可输入,name换成你想删的环境名。

conda env remove -n name

通过conda创建gurobi环境

下载gurobi

conda install -c gurobi gurobi

激活gurobi
通过学术申请，获得免费gurobi权限，gurobi通过邮箱发送密钥，先进入所在的虚拟环境，在命令行中复制密钥回车即可激活
验证是否激活：
在python例import gurobi，如果没有报错则已经成功激活gurobi
在这里插入图片描述

升级gurobi

conda update gurobi

指定版本

conda install gurobi=9.1.2

删除已有版本

conda remove gurobi

在服务器后台运行程序

参考博客：Linux服务器使用 nohup & 和 setsid命令开启/关闭后台运行进程的方法
感谢大佬！！

创建后台进程

由于远程连接服务器，在电脑关机或网络断开的时候，可能会导致断开连接，程序在服务器运行终止，而我们又不可能长时间盯着电脑，因此创建后台进程，保证服务器可以持续运行程序，不受远程连接的网络等影响
以python程序exp3.py为例：

nohup python exp3.py &

则会出现创建的进程号：如，此进程号为551481

[1] 551481

如果是.sh脚本，则为

nohup sh exp3.sh &

&：是指在后台运行，但是当用户退出（挂起）的时候，命令会自动跟着结束。
nohup：是指不挂断运行，可以使命令永久的执行下去，和用户终端没有关系。
将 nohup 和 & 结合使用，就可以实现使命令永久地在后台执行了。

查看后台进程

ps -aux|grep 程序名| grep -v grep

如上例：

 ps -aux|grep exp3.py| grep -v grep

命令行输出进程信息

xiaoqin+  551481  100  1.4 3768868 3705536 pts/11 R   10:15   1:01 python exp3.py

可看到进程号为551481，文件为exp3.py

关闭后台进程

通过查询到的进程号，关闭后台进程

kill 551481

强制终止进程

kill -9 551481