Deep Neural Networks for YouTube Recommendations

Deep Neural Networks for YouTube Recommendations

文章主要介绍了youtube的视频推荐系统。根据检索的两个阶段，文章分成两大块，第一步是召回模型，第二步是基于dnn的排序模型。
同时，文中也介绍了在设计、迭代和维护如此大型的推荐系统时的一些经验。

INTRODUCTION

youtube视频推荐主要有三点挑战：

1. 规模
2. 新鲜度（freshness
3. 噪声
   第一点是显然的，第二点是指系统需要对用户上传的新视频和用户最新的动作都能及时响应。第3点是指由于稀疏性和外部不可见的因素会导致用户的历史行为难以预测。用户满意程度的基线（ground truth）难以获取，所以转而对包含噪声的隐式反馈进行建模。所以推荐算法必须足够健壮

SYSTEM OVERVIEW

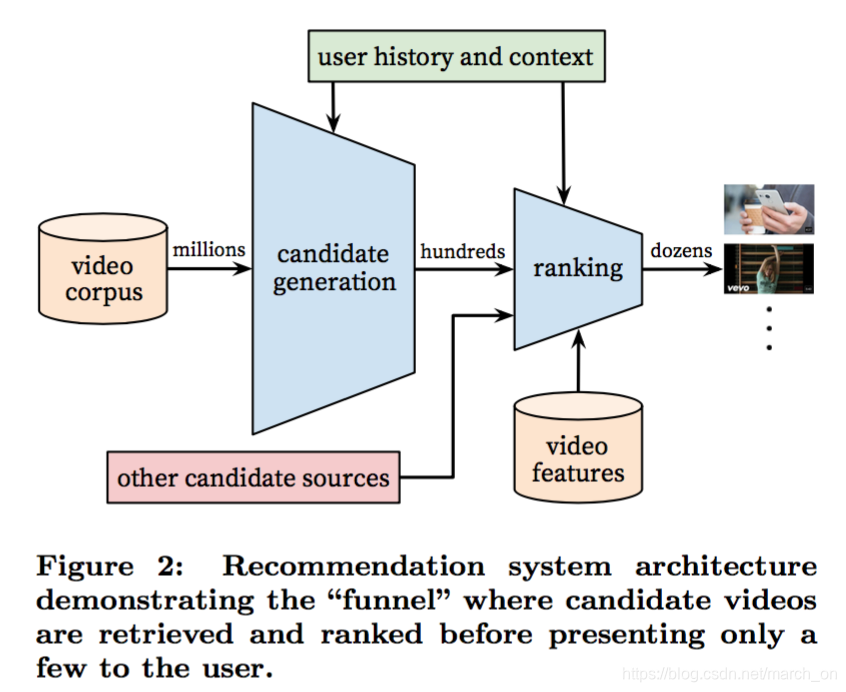
整个推荐系统包含两个神经网络，一个召回模型，一个排序模型

召回模型通过协同过滤来实现比较宽泛的推荐，使用的特征包括用户观看过的ID、查询中的tokens和人口统计特征，这些特征都比较粗糙。

而如果要提供最好的推荐，则需要一些更加精细的特征来区分候选集之间的排序。
排序网络根据用户、视频的各种更加精细的特征 使用某个目标函数来实现对视频的打分。最后得分越高，用户看到的排位越靠前。

在开发过程中，作者线下使用了很多指标（准确率、召回率、排序损失等），但是决定一个模型真正效果的还是线上AB实验。这是因为线上实验的很多指标并不一定和线下指标有关。

召回

作者提到在基于DNN的召回模型之前他们使用的是Scaling up to large vocabulary image annotation，这是一个基于rank loss的矩阵分解模型。召回模型在初期的迭代中就是在模仿 该模型的分解行为，使用浅层网络，只对用户的历史观看视频进行embedding。从这个角度，该网络可以看做分解方法的非线性推广。

将推荐作为分类问题

作者将推荐问题建模成分类问题。
预测 在时刻$t$发生的观看行为$w_t$ 属于哪个类，要根据用户U和上下文C 对视频库$V$ 中的每个 视频i进行预估

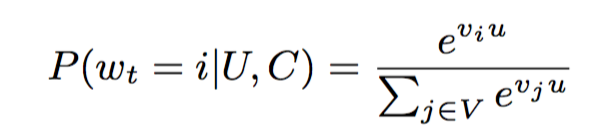
$U\in R^N$ 是用户、上下文对的embedding向量。$V_j\in R^N$ 是视频的embedding向量。该模型就是学习基于用户行为和context表示的用户embedding，该embedding可以用来区分videos。

作者使用观看中隐式反馈来训练模型。一次完整的观看作为一个正样本。这么做的原因是用户的隐式反馈更多，即使是长尾中的视频也能被推荐，相反，显式反馈更稀疏。

为了提高训练效率，作者使用采样方法。从样本分布中采样出若干视频做负样本，并且通过重要性权重进行修正（rely on a technique to sample negative classes from the back- ground distribution (“candidate sampling”) and then correct for this sampling via importance weighting）。实践时作者采样了上千个负样本。作者没有使用层次softmax，因为实验效果不好。
这种方法会对两个没有关联的类别进行分类，使得分类更困难，影响效果。
在线上，需要选择用户最可能观看的N个视频。因为线上不需要根据softmax 输出计算似然函数，所以可以直接在内积空间使用最近邻搜索来找到距离最近的N个视频。线上实验表明最近邻算法影响不大。

Model Architecture

受Distributed representations of words and phrases and their compositionality 启发，视频词典（fixed vocabulary） 中的每个视频都学习一个embedding向量。用户的观看历史是一个不定长的视频ID序列，然后每个ID都被embedding成一个向量，然后输入给DNN。因为DNN需要固定的输入长度，avg pooling 的效果在几个pooling方法(sum/avg/max)中最好。

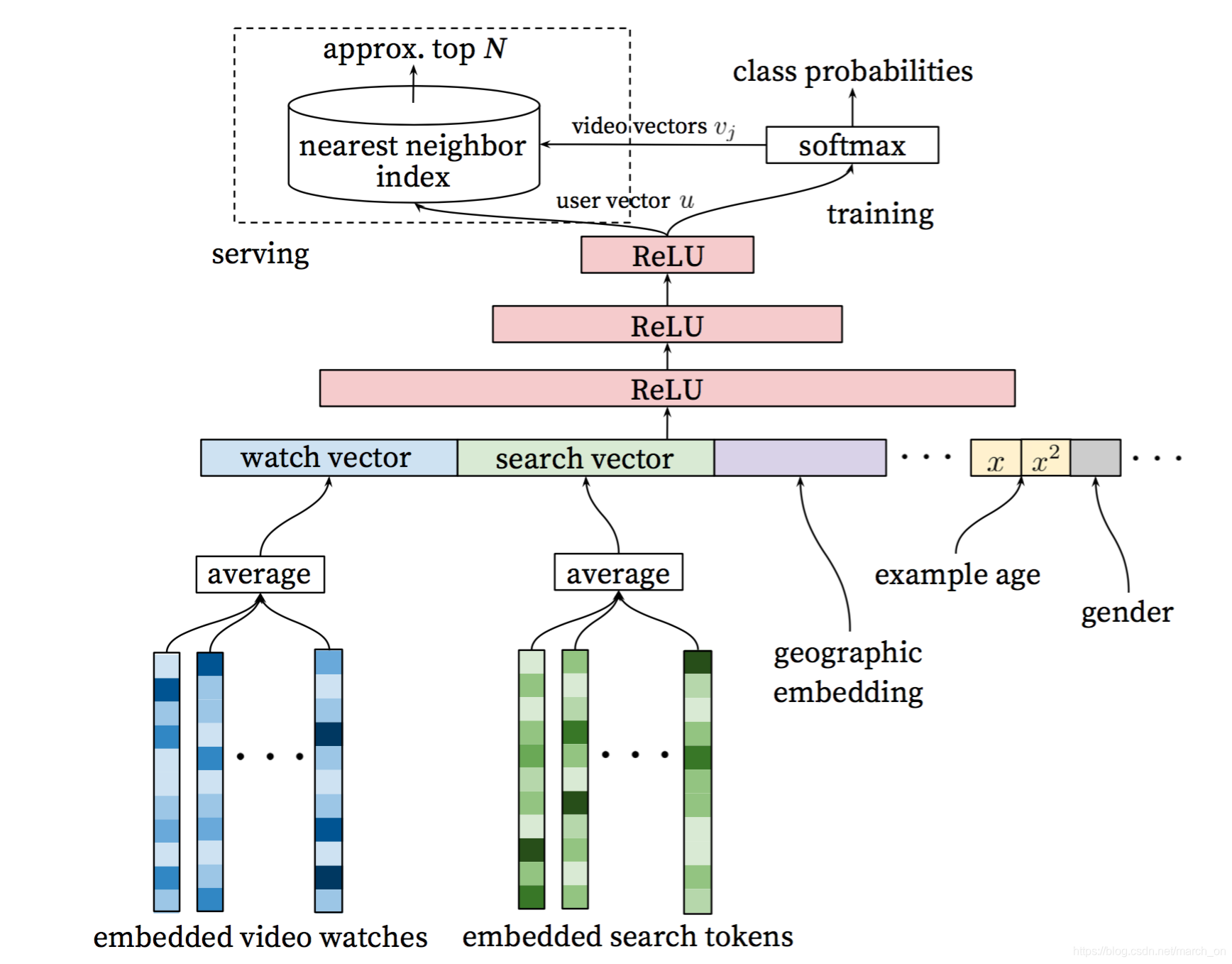
Heterogeneous Signals

历史搜索和历史观看的处理差不多，先被分词成unigrams 和 bigrams，然后都被embedding，最后取平均，得到固定长度的历史查询embedding向量。人口统计学特征在对新用户进行推荐时很重要，他们的地理位置和设备类型都被embedding，二值特征和连续特征（性别、登录状态、年龄）都被直接输入给网络，然后归一化到0，1区间。

为啥性别、登录状态这种二值离散特征也被当做连续特征来处理？

“Example Age” Feature

用户总喜欢点新视频，即使是不相关的。机器学习系统经常对过去的样本有偏置，毕竟系统是在过去的数据上训练去预测未来。视频流行度的分布不是静态的，而推荐系统给出的多项式分布只是反应出训练时间窗口内的平均观看似然。为了修正这个，作者在训练时将**the age of the training example ** 加入到样本。 当了线上会置0，表明模型是在对训练窗口的截尾进行预测。

比如训练时间窗口是1201-1214，那么1201的样本时间是14天？

但是下图为啥是上传之后的天数？为啥还会有负数

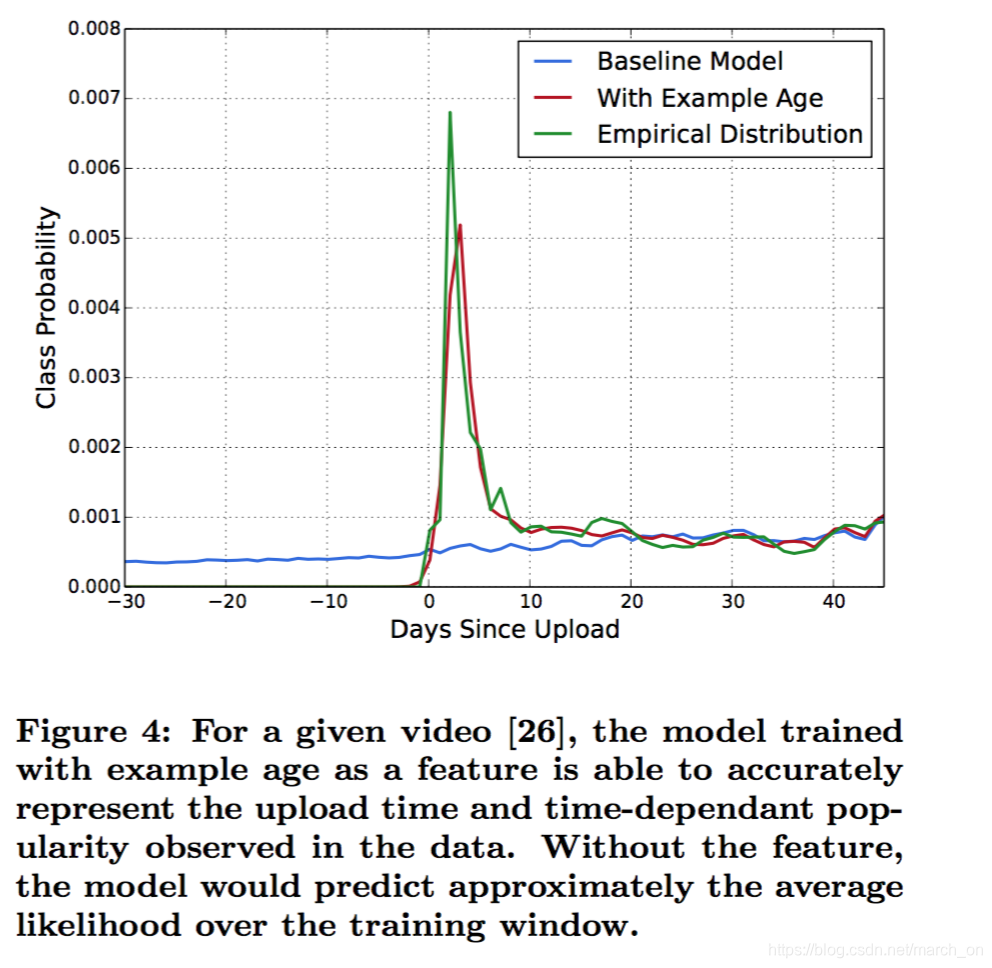
Label and Context Selection

推荐系统中通常会涉及到定义一个代理问题 然后将这个问题上的结果应用到某个场景中，比较经典的案例是准确预估电影评分可以使推荐更有效。
作者发现代理问题的选择对A/B测试的效果影响很大， 但是却很难离线评估。

这一段不是很理解。

训练样本是从所有youtube上的观看产生的，即使是嵌入在其他网站上的观看，而不仅仅是我们的推荐上产生的观看。否则，新视频就很难被刷出来，同时，推荐系统也会过度倾向于向利用(exploitation)。

为啥新视频很难被刷出来？因为新视频的行为数据较少，在推荐系统中的得分会比较低，所以很难刷新出来？

如果用户通过其他方式发现了video， 我们需要通过协同过滤将这个发现快速传播起来。

另外一个观察就是每个用户生成固定数目的训练样本可以提高线上指标，这样每个用户在损失函数下的权重都是一样的。这样可以避免高度活跃的用户对损失的影响过大。

还有一些反直觉但是必须注意的是必须避免某些信息被模型所利用，防止模型学习到网站结构，对代理问题产生过拟合。

举个例子：
一个用户刚搜索了 taylor swift。因为我们的问题是预测用户下一个观看的视频，那么模型使用这个信息后就会把那些在taylor swift 搜索结果页面出现的视频预测为最可能观看的视频。毫无疑问，将用户最近一次搜索的结果作为首页推荐，体验肯定很差。
通过去掉序列信息，使用无序的tokens来表示查询，模型就不能直接意识到label的来源（不太明白）

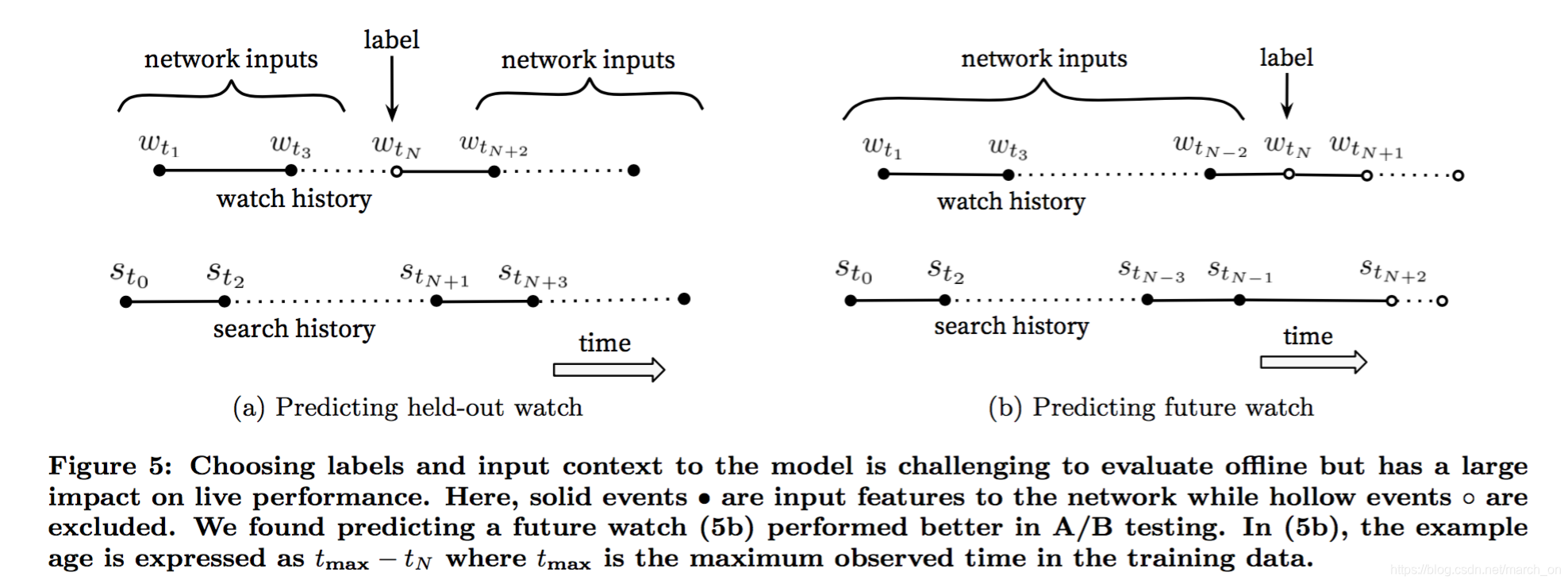
视频的自然观看模式通常会导致非常不对称的co-watch 概率，比如电视剧是顺序观看的，用户发现艺术家时都是先从最流行的开始，然后聚焦到某个细分流派。
所以在预测用户的下一个预测时 不能只是简单地从历史观看中随机采样一个作为label，剩余的作为输入。

而是采样的视频之前的观看作为输入才行。

协同过滤算法都是随机选择一个item，使用用户历史上的item来预测被选择的item。这样会泄漏未来的信息，并且忽视非对称的消费模式。相反，作者回滚用户的历史行为，随机选择一次观看，只有在被选择的观看之前发生的行为才被作为输入。
这样做的线上效果也会更好。

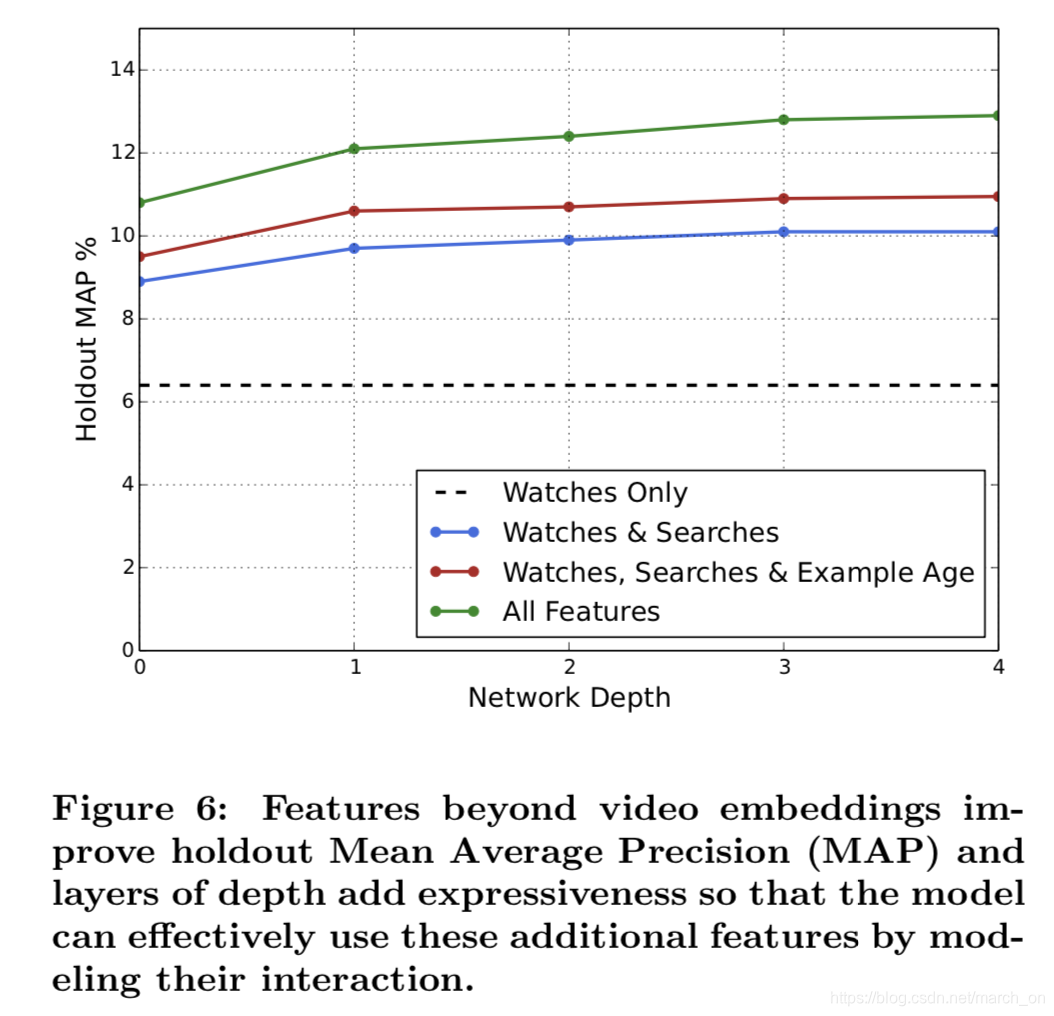
特征和深度实验

特征+模型深度都可以明显提高效果
实验中，作者使用的词典大小如下：
视频1M，搜索词 1M， embedding向量维度256， 历史观看 长度50， 历史搜索长度50

排序模型

排序阶段因为候选视频少了很多，所以可以使用更多特征来描述视频和用户。
作者使用的神经网络和召回模型的结构类似，输出层使用LR来对视频打分。最终排序的目标函数一直在根据AB测试的结果调整， 但是一般都是每次曝光的期望观看时间的函数。

通过CTR来排序通常会提高带有诱导性的但是用户并没有看完的视频的排名，而基于观看时间则能更好的衡量参与程度。

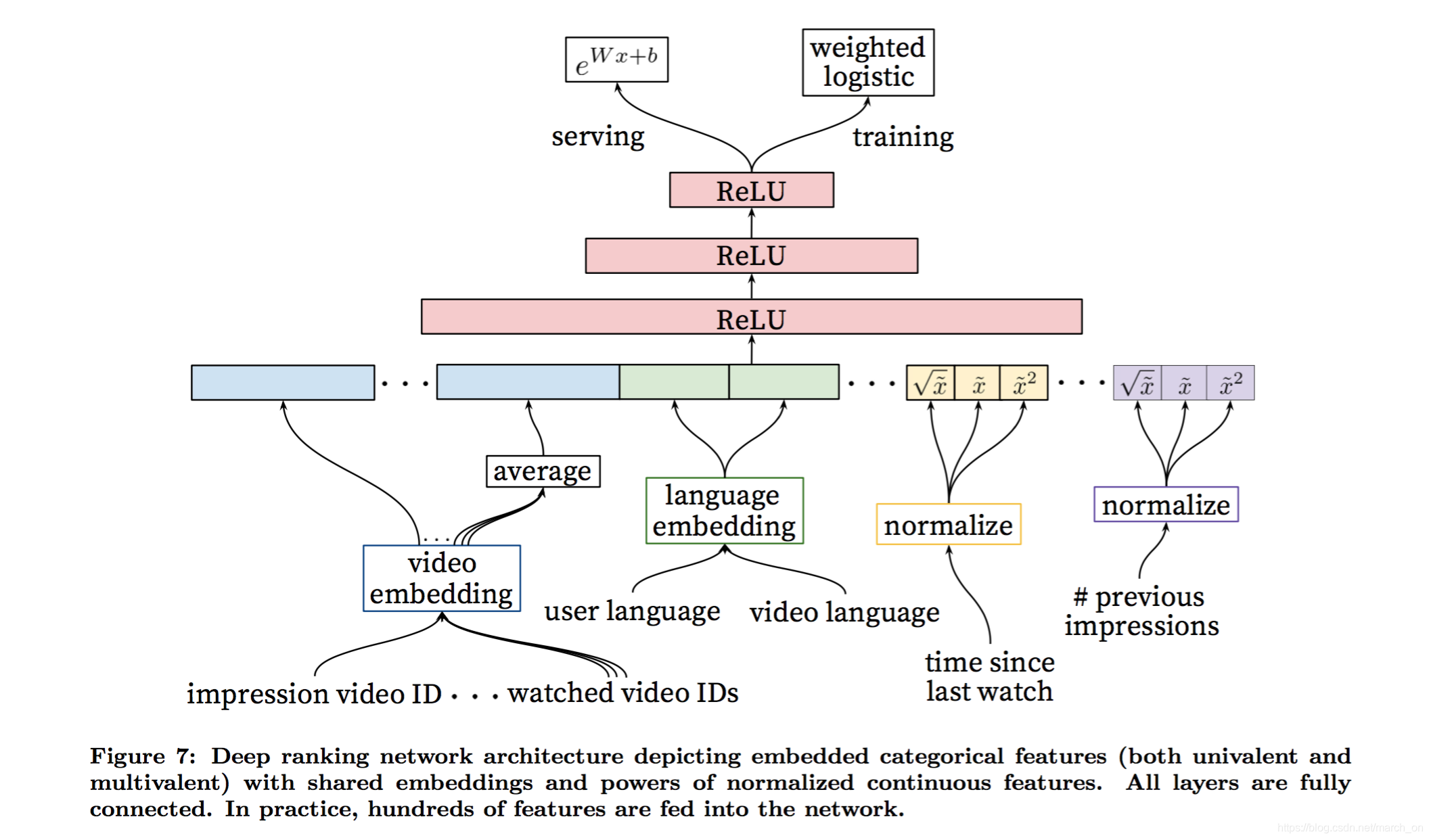
特征表示

作者按传统分类方式将特征分成两种：连续/顺序（ordinal)特征和离散特征。文中使用的离散特征的基数变化很大。从binary 特征（是否登录）到百万取值（最后一个查询）。
根据特征是同时只有一个取值还是有多个取值 进一步分成了单值特征或者多值特征（one hot vs multi-hot)。比如当前展示的视频的ID就是一个单值特征，用户最后观看的N个视频的ID则是一个多值特征 。

也可以根据特征是否描述item的属性（即impression）或者user/context（即查询）的属性来划分。

Query features are computed once per request while impression features are computed for each item scored.

查询特征 每个请求计算一次，展现特征则每个item都要计算。

Feature engineering

尽管DNN可以减轻特征人工特征工程的压力，但是数据还是需要经过处理之后才能直接输入网络。

主要挑战在于如何表示用户行为序列，以及这些行为如何和当前的曝光有相关联。
作者发现最重要的信息是那些用户之前与当前的item（视频）或者相似的item之间产生的行为。和别人在广告上的经验相似（Practical lessons from predicting clicks on ads at facebook）。比如，用户在当前视频所属的channel上的历史行为。比如这个用户 看了多少这个channel的视频。用户最后一次观看这个topic的视频是什么时候，这些描述用户在当前item或者相似item上的历史行为的连续特征特别有用，因为他们在不相干的item上泛化效果很好 。 同时也发现，将召回阶段的信息传播到排序阶段也很有用，比如这个视频的来源，评分是多少。

描述视频的历史展现频率的特征对向推荐系统引入搅拌（churn）效果很重要，即连续的请求不返回相同的列表。 如果系统给用户推荐了某个视频而该用户没有看，那么在下次请求时 这个视频的排序会下降。

Serving up-to-the-second impression and watch history is an engineering feat onto itself outside the scope of this paper, but is vital for producing responsive recommendations.

秒级的曝光和观看历史对生成及时的推荐很重要。

Embedding Categorical Features

和候选集生成阶段的处理方式相似，字典中的每个ID都有一个embedding向量，维度和词典的log 成正比（approximately proportional to the logarithm of the number of unique values）。这些词典是在训练前统计一遍数据得到的。基数非常大的ID 特征 通过对点击展现次数进行排序选取topN 个ID。 词典外的词汇都会映射到下标为0的embedding向量。
和候选集生成阶段一样，多值离散特征 取平均之后输入给DNN。

更重要的是，相同ID空间的离散特征共享embedding 。比如存在一个全局共享的视频ID的embedding空间，许多特征都会使用这个embedding空间，比如展现的视频ID，用户最后观看的视频ID ，作为种子生成该推荐的视频的ID 。

尽管是统一embedding，但是各个特征是分开喂给网络的，上层网络会学习到自个的表示。

Sharing embeddings is important for improving generalization, speeding up training and reducing memory requirements.

共享embedding 对提高泛化、加快训练和降低内存消耗都很重要

Normalizing Continuous Features

神经网络对特征的缩放和分布很敏感，但是决策树却并不敏感。作者发现合适的normalization方法对收敛很重要。

特征x的分布是$f$, 通过以下方法将x转换为$\hat{x}$ :
使用累积分布$\hat{x}={\int }_{-\infty }^{x}df$ 对特征进行缩放，使其 均匀分布在[0,1)区间。积分通过线性插值法对特征值的分位点进行估算，分位点是在训练前对数据做一次遍历计算得出。

这个没看懂

除此之外，作者还是用$x^2$和 $x^{1/2}$ 作为特征，提高网络的表达能力，因为加入了超线性和次线性特征使得模型的表达能力更强。
将连续特征的幂次 值加入模型可以提高线下效果。

Modeling Expected Watch Time

目标是预测样本的期望观看时间，如果视频被点击则是正样本，否则是负样本。

为了预测期望观看时间，作者使用加权LR（weighted logistic regression )。损失函数是交叉熵损失，但是，正样本的权重是用户的观看时间，负样本的权重是1。这样LR的odds 就是 $\frac{\sum Ti}{N-k}$ ，
N是样本数，k是正样本数，Ti 是观看时间。假设正样本比例很小，那么学习到的odd 是ET,P是点击概率， E[T]是曝光的期望观看时间。因为P很小，所以该式近似于E[T]。线上预估时使用指数函数$e^x$作为激活函数，给出odd。

odd是啥？？

Experiments with Hidden Layers

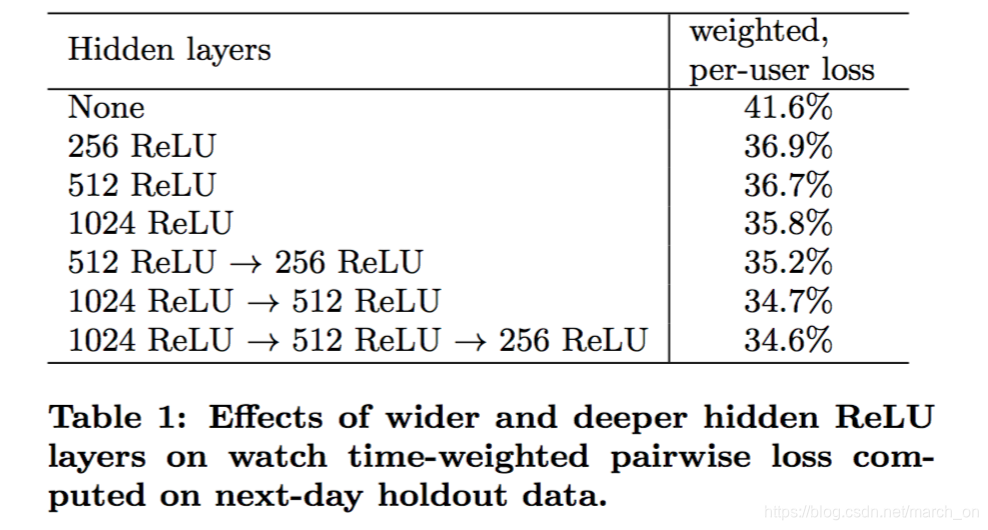
上表是不同的网络结构在下一天的holdout 数据上的效果。上述效果是考虑在同一个页面上展现给用户的正例和负例来计算得到的。首先对这两个展现计算分数，如果负例的得分高于正例，那么这个正例的观看时间就是被错误估计的观看时间 ， weighted , per-user loss 是所有的被错误估计的观看时间占holdout数据所有观看时间的比例。

可以看出，增加网络深度和宽度可以提升效果。

对于1024-512-256网络，作者发现只输入归一化的连续特征，没有对应的power， loss增加了0.2%。同一网络，如果正样本和负样本权重相同，loss 增加了4.1%。

Conclusion