集成学习Ensemble Learning

1.集成学习概念

在有监督学习过程中，我们希望训练得到一个各方面表现都很好的“稳定”的模型。但实际训练过程中，我们常常训练得到的是在某个方面表现较好的模型，这样的模型可以训练出很多，他们的擅长的方面也不完全一样。这时候我们就会想要通过“模型组合”或者叫“模型融合”的方式来获得更好更稳定的模型。这个过程也叫集成学习。

集成学习是通过多个“个体学习器”的组合，获得更优泛化性能更好的学习器。
根据组合的个体学习器的类型异同，集成过程分为同质集成和异质集成。
根据个体学习器的生成方式不同，集成学习分为两大类。
1）个体学习器之间存在强依赖关系，必须串行生成的序列化方法：boosting类算法。
2）个体学习器之间不存在强依赖关系，可以同时生成的并行化方法：bagging和随机森林。

2.什么是boosting、bagging

boosting:

boosting算法是一族将弱学习器提升成强学习器的算法。

【弱学习器】是指准确率略高于随机算法（50%）的学习器，
【强学习器】是准确率很高的学习器。

在模型训练中，弱学习器往往比强学习器更容易得到，所以有了能否将弱学习器提升（boosting)成强学习器的疑问。提升（boosting)类算法应运而生，这类算法，从一个弱学习器出发，通过多次反复（样本调权）训练，得到多个弱学习器，再将这些弱学习器通过某些策略组合，最后得到一个强学习器。
获取弱学习器的算法：
大多数的提升算法，都是通过对样本权重进行调整去获取多个弱学习器的。调权的核心原则是降低上一次分类正确的样本的权重，提升上一次分类错误的样本的权重，这样使得后一轮的迭代模型能够更加关注上一轮分类错误的样本。
弱学习器组合算法：
1）线性组合：准确率高的提权，准确率低的降权，加和。代表算法Adaboost。

2）提升树（boosting tree)：通过拟合残差的方式逐步减小残差，将每一步生成的模型叠加得到最终模型。

提升树模型采用加法模型（基函数的线性组合）与前向分步算法，同时基函数采用决策树算法，对待分类问题采用二叉分类树，对于回归问题采用二叉回归树。提升树模型可以看作是决策树的加法模型：

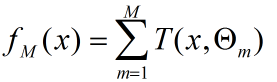
　　其中T（）表示决策树，M为树的个数， Θ表示决策树的参数；
　　提升树算法采用前向分部算法。首先确定f0(x) = 0,第m步的模型是：

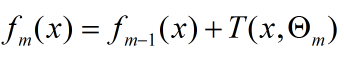
　　对决策树的参数Θ的确定采用经验风险最小化来确定：

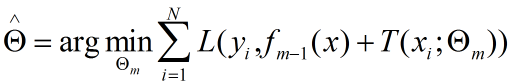
　　对于不同的问题采用的损失函数不同，在决策树中使用的就是0/1损失函数，这部分的推导和前面的adaBoost中的关于分类的推导相同，不做详细介绍。对与回归问题来说，一般采用平方误差函数。
　　对于回归问题，关于回归树的生成可以参考CART算法中回归树的生成。对于以下问题：
　　输入：T={(x1,y1),(x2,y2),......,(xn,yn)},

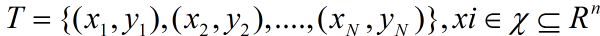
　　输出：fM（x）
　　对于一颗回归树可以表示为：

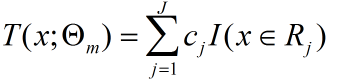
　　那么在前向分步算法的第m步中也就是求解第m个回归树模型时，为了确定参数需要求解：

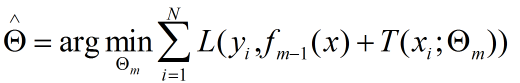
　　当采用平方误差损失函数时，损失函数为：

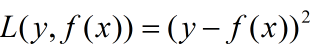
　　将上面的待求解式子带入到下面的平方误差函数中可以得到以下表达式：

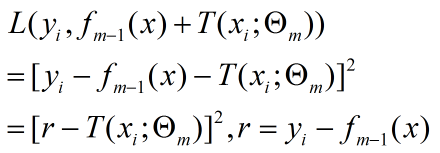
　　这就表明每一次进行回归树生成时采用的训练数据都是上次预测结果与训练数据值之间的残差。这个残差会逐渐的减小。

算法流程：

（1）、初始化f0（x） = 0；

（2）、对于m=1,2,…,M

（a）按照 r= yi - fm-1(x)计算残差作为新的训练数据的 y

（b） 拟合残差 r 学习一颗回归树，得到这一轮的回归树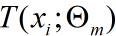

（c） 更新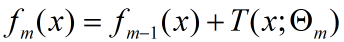

（3） 得到回归提升树：

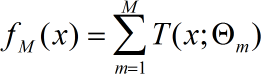
bagging
bagging即套袋法。
套袋法过程：
1.抽样（选取训练集），抽K次，每次从原始样本中随机抽取Nk个样本（每次抽的样本之间可能有重复，因为池子都是原始样本）。
2.抽出了K个样本集合进行训练，可根据数据分布分别选择不通的算法，得到K个模型。
3.如果是分类问题：对于同一个样本，不同模型之间进行投票，取准确率高者。如果是回归问题，计算上述模型的准确率均值作为最后的结果。（所有模型的重要性相同）

下图是算法过程。

boosting与bagging的区别与关联

1.样本选择和样本权重：

bagging：每个训练集都是有放回的选取的，简单说就是抽样的池子是一样的，这样每次抽出来的样本可能会重复。每个训练集之间是独立的，谁也不必关心谁。训练集中每个样本的权重是一样的。
boosting：每个训练集的样本都是一样的，不一样的是每个训练集中样本的权重可能不一样。下一个训练集的生成依赖上一个训练集的训练结果，根据上一轮训练的结果，调整本轮中样本的权重，上轮训练中分类错误的样本，在本轮中提权，上轮训练中分类正确的样本，在本轮中降权，生成新的训练集。

2.组合的学习器之间的权重：

bagging: 组合的学习器之间的权重是一样的。
boosting:组合的学习器之间，准确率高的权重高，准确率低的权重低。

3.并行计算：

bagging:每个分类器可以并行训练。
boosting:下一个分类器依赖上一个分类器的训练结果，只能串行训练。

4.分类器目标：(yi表示预测结果，ya表示预测结果的期望（平均值），ha表示实际label的平均值）

bagging:降低方差(variance)。(yi-ya)^2
boosting:降低偏差（bias)。(yi-ha)^2

以下待补充：

偏差和方差

为什么说bagging是减少variance，而boosting是减少bias？

GBM,lightGBM,GBDT,XGBOOST，Adaboost算法