
目录
1. 概念
一个CRC计算的小工具:
在了解CRC如何工作之前,我们需要先了解几个概念。
1.1 什么是异或运算
异或运算是一种逻辑运算,用符号"⊕"表示。当两个二进制位不同时,结果为1;当两个二进制位相同时,结果为0。
| 结果 | 运算公式 | ||
| 0 | 0 | 0 | 0⊕0=0 |
| 0 | 1 | 1 | 0⊕1=1 |
| 1 | 0 | 1 | 1⊕0=1 |
| 1 | 1 | 0 | 1⊕1=0 |
相同得0,相异得1
1.2 什么是多项式
一个多项式是由变量(如 x)和系数(常数)通过加法、减法、乘法及非负整数次幂运算构成的表达式。

在 CRC 算法中,二进制数据被映射为多项式,举个例子,假如现在有二进制数10110011,其中二进制数的每一位对应的是系数(),则对应多项式为:
1· + 0·
+ 1·
+ 1·
+ 0·
+ 0·
+ 1·
+ 1
可简写为: +
+
+
+ 1
在CRC中用到的除数,正是由多项式的各项系数组成。
1.3 什么是模2运算
CRC 使用模 2 多项式算术。模2运算(Modulo-2 Arithmetic)是一种在二进制数(只有0和1)上定义的运算规则体系。
1.3.1 加法/减法运算
不考虑进位(加法时)或借位(减法时),其核心操作等价于异或(XOR)运算。
| 加法运算公式 | 减法运算公式 | ||
| 0 | 0 | 0⊕0=0 | 0⊖0=0 |
| 0 | 1 | 0⊕1=1 | 0⊖1=1 |
| 1 | 0 | 1⊕0=1 | 1⊖0=1 |
| 1 | 1 | 1⊕1=0 | 1⊖1=0 |
注意这里是二进制加减,不要将其当成自然数加减了
1.3.2 乘法运算
规则与普通二进制乘法(逻辑与 / AND)相同。
| 程法运算公式 | ||
| 0 | 0 | 0⊗0=0 |
| 0 | 1 | 0⊗1=0 |
| 1 | 0 | 1⊗0=0 |
| 1 | 1 | 1⊗1=1 |
1.3.3 除法运算
模 2 除法相对于普通的算术除法,主要的区别在模 2 除法,它既不向上位借位,也不比较除数和被除数的相同位数值的大小,只要以相同位数进行相除即可,举个例子:
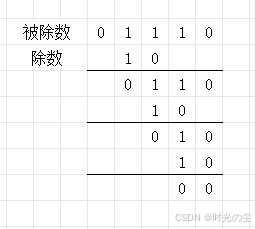
需要注意几点:
① 对齐:将除数与被除数的最高有效位对齐。
② 异或:如果对齐后的被除数部分当前最高位是1,则在该步的商记1,并用除数对当前被除数部分进行模2减法(XOR)。
③ 下移:将下一位被除数位带下来,形成新的部分被除数。
④重复:重复步骤2和3,直到处理完所有被除数位。
⑤ 结果:最终得到的商就是模2除法的商,最后剩下的部分(位数比除数少一位)就是余数(Remainder)。
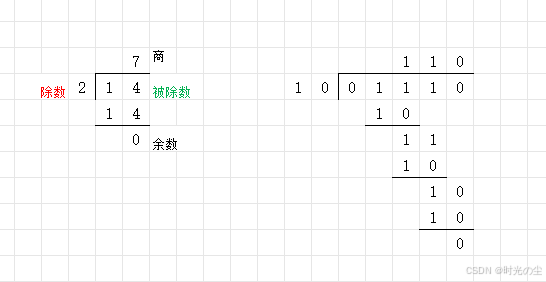
上面那样看着不明显,我们和十进制放一起看一下:
上面概念了解完了,下面我们来看看什么是CRC。
2. CRC运算
循环冗余校验(Cyclic Redundancy Check,CRC) 是一种广泛应用于数据通信和存储系统中的错误检测技术。它利用多项式除法生成一个固定大小的校验码(CRC 码),并将其附加到传输的数据上,使接收方能够验证数据的完整性。其特征是信息字段和校验字段的长度可以任意选定,当检测原始数据在传输或存储过程中发生的意外改变,它能识别错误但不能纠正错误;一旦检测到错误,通常会触发重传请求。
那么CRC是如何使用的呢?这里我们举个例子,以这个例子进行展开描述:
我们来计算0x1C的CRC-8的校验结果:
数据串:0001 1100
多项式:
+
+
+ 1
2.1 步骤一:展开多项式获得CRC除数
多项式: +
+
+ 1,展开后就是:
1· + 0·
+ 0·
+ 0·
+ 0·
+ 0·
+ 1·
+ 1·
+ 1
对应的除数就是二进制:
除数:1 0000 0111
2.2 步骤二:数据末端加0
数据串也就是被除数,根据多项式的最高此项在后方补0,多项式最高是几次就加几个0,根据除数可知最高此项为8,也就是补8个0,此时被除数为:
被除数:0001 1100 0000 0000
2.3 步骤三:数据运算
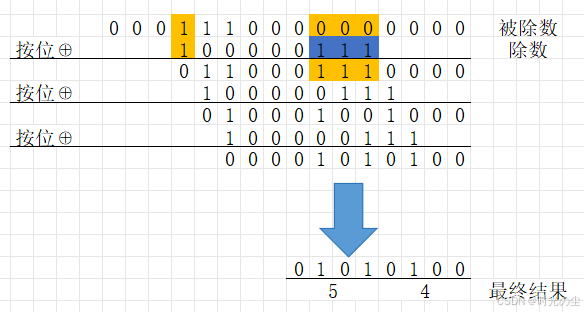
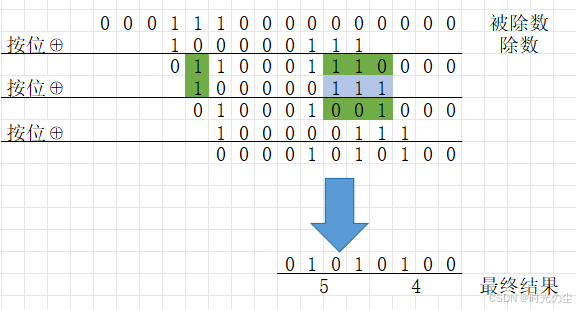
根据1.3.3的除法运算进行运算,将除数与被除数的最高有效位对齐:
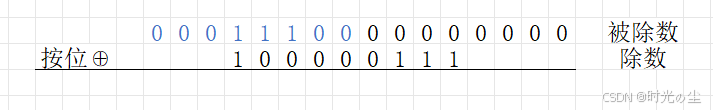
进行按位异或操作:
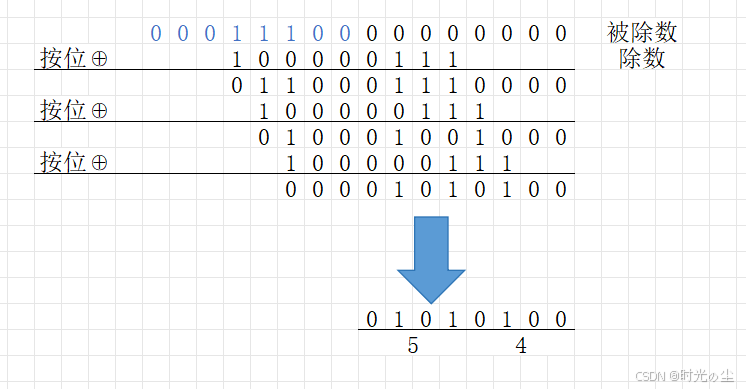
使用上面的校验工具看一下:
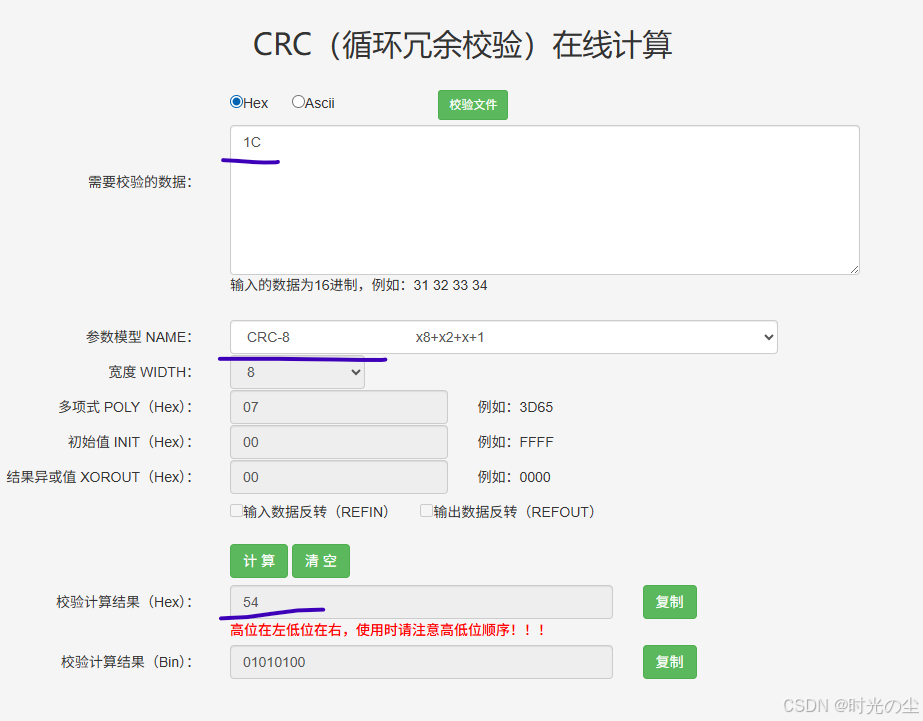
2.4 结果
找到我们刚才的例子:
计算0x1C的CRC-8的校验结果:
数据串:0001 1100
多项式:
+
+
+ 1
此时我们就可以得到:
数据串(被除数):0001 1100 0000 0000
多项式(除数): 1 0000 0111
校验和: 0101 0100
这里我们在使用过程中想要发送带有CRC校验的数据,即将校验和添加到原始的数据串后面即可:
数据串:0001 1100
校验和:0101 0100
带有CRC校验的数据:0001 1100 0101 0100
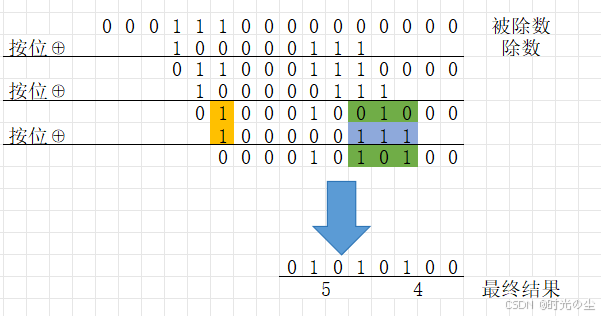
注意!!!
这里有一点需要了解,校验和的位数不是随便取的,校验和的位数等于最高次幂的系数,也就是除数的位数-1,例如我们上面最高次幂为8,因此我们校验和最终位数取了8位,我们在举一个例子:
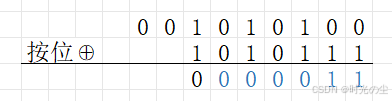
此时我们若是取校验和,就需要取蓝色部分。
以上就是CRC相关简单的运算过程,下面我们做一些拓展。注意拓展的这四个名词是为嵌入式单片机服务的,如果只是单纯的使用CRC计算,上面这些就可以了。
3. 拓展:初始值、结果异或值、输入反转、输出反转解释
下面是一些常见的CRC参数模型,可能你发现了,除了我们上面提到的,还有四个名词没有使用到,即初始值、结果异或值、输入反转、输出反转:
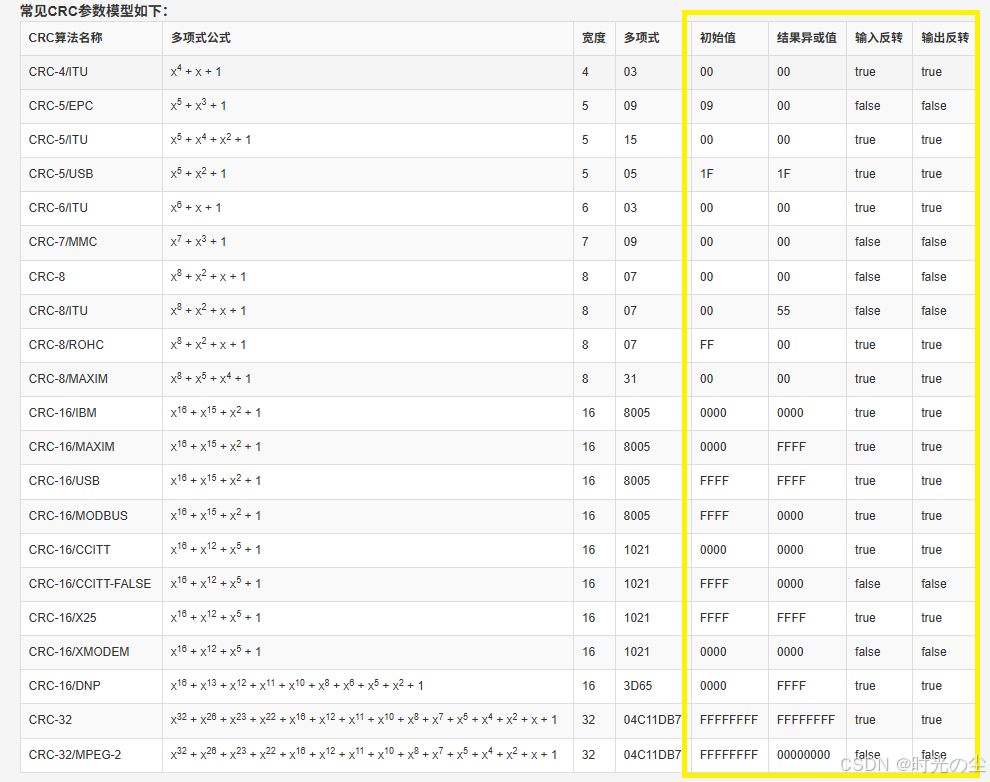
这些有什么作用呢?我们还是举例进行说明,我们先回到最开始的例子,以它来数据一下假如这四个名词后的运算流程:
计算0x1C的CRC8的校验结果:
数据串:0001 1100
多项式:
+
+
+ 1
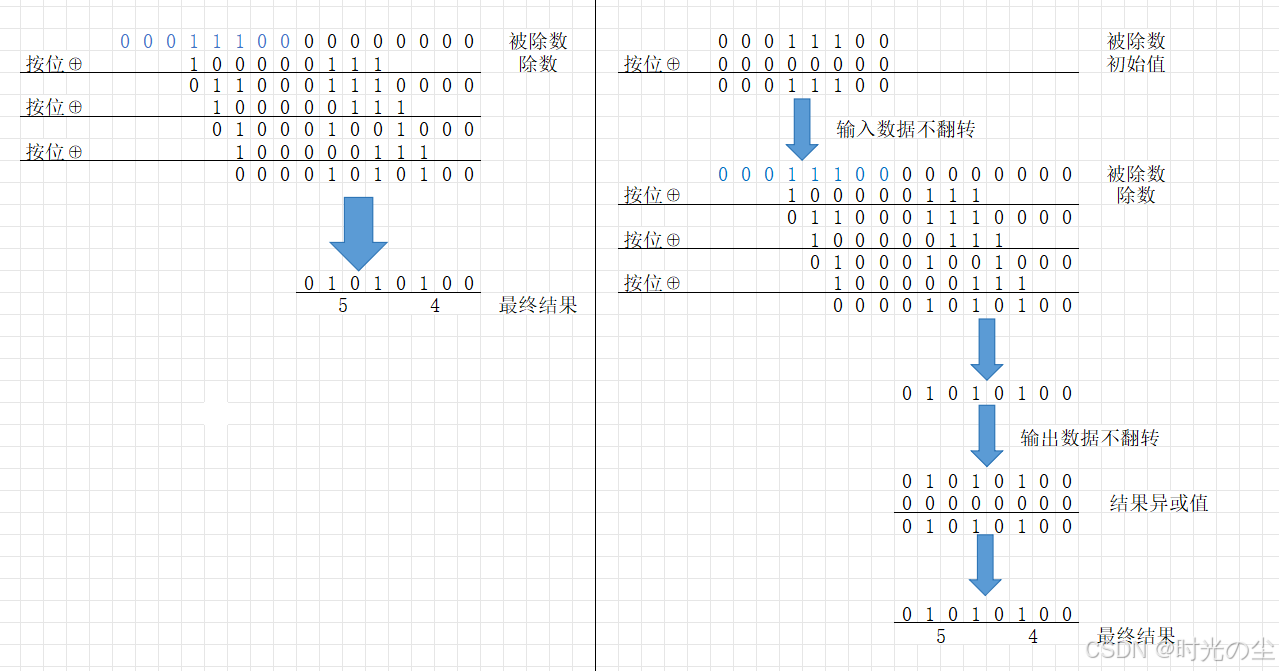
按照我们上面的运算过程:
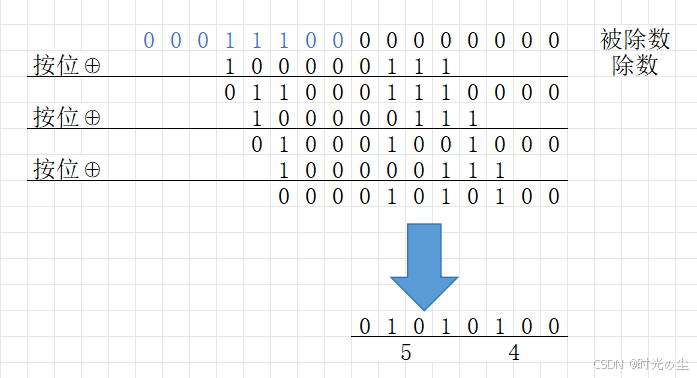
那么我们带入表中的四个数据,结果还会是这样吗?

根据表中数据,结果异或值、输入反转、输出反转:
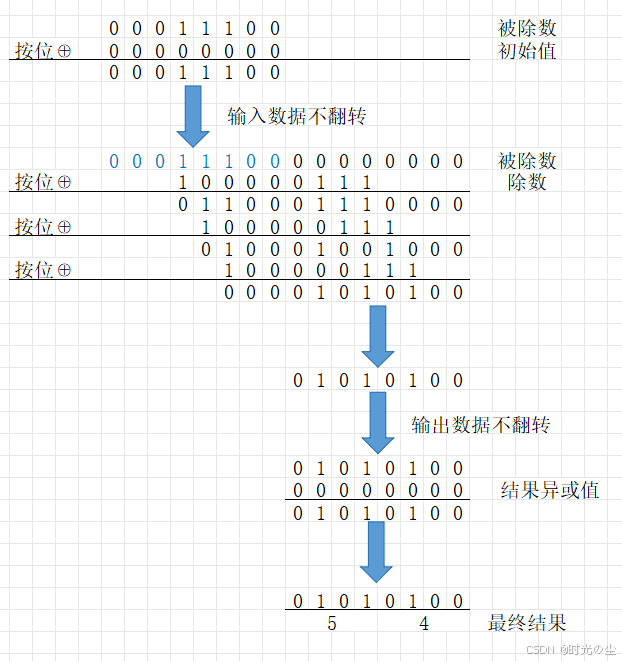
可以看出最终结果没有发生变化:
3.1 初始值
初始值(Initial Value 或 INIT)是指在开始处理数据之前,预先填充到CRC寄存器(或称为移位寄存器)中的值。
增加初始值可以避免全零陷阱,全零的CRC校验码在传输或存储中可能与“无数据”或“数据缺失”的状态混淆。使用非零初始值(尤其是非全零的特殊值)可以确保即使数据是全零,计算出的CRC也不会是零(除非数据恰好满足某种条件),提高了校验码的区分度。
各种标准的CRC算法(如CRC-16-CCITT,CRC-32,CRC-16-MODBUS)都明确规定了必须使用的初始值。初始值是区分不同CRC变体的关键参数之一。只有使用相同的初始值(以及相同的生成多项式、输入反转、输出反转、结果异或值),不同系统计算出的CRC校验码才能一致。
3.2 结果异或值
结果异或值 (Final XOR Value / XOROUT)在计算完整个数据的CRC值后,但在输出最终校验码之前,将这个值按位异或 (XOR) 到CRC寄存器(即当前的CRC结果)上。
效作用和初始值差不多,只不过一个是在数据处理之前,一个是在数据处理完成以后。
3.3 输入反转
输入反转 (Input Reflection / REFIN)在将每个输入数据字节送入CRC计算核心(通常是移位寄存器)进行处理之前,是否先反转(Reflect)该字节内的比特顺序。
反转操作就是将一个字节(8位)的最高位 (MSB) 和最低位 (LSB) 交换,次高位和次低位交换,依此类推。相当于将字节内的比特顺序颠倒过来。举个例子:假如现在有 0x11001001,反转后就是 0x10010011,也就是 12345678 变成 87654321。
这样做的目的,是因为早期硬件CRC计算电路(使用线性反馈移位寄存器)有时采用不同的移位方向(左移 vs 右移)。输入反转提供了一种软件方式,使得即使底层计算逻辑是按特定方向设计的,也能兼容处理不同比特顺序(MSB-first vs LSB-first)的数据流。
3.4 输出反转
输出反转 (Output Reflection / REFOUT)在应用了结果异或值之后,但在输出最终的CRC校验码之前,是否反转整个CRC寄存器值的比特顺序。
原因和输入类似。
简单来说,这四个名词出现的原因,是解决硬件实现差异(移位方向、比特顺序)和避免特殊值(全零CRC)的问题,确保遵循同一标准的系统计算出的CRC校验码完全一致。
4. 拓展:C语言代码编写一
还是以我们上面的举例进行了解:
计算0x1C的CRC8的校验结果:
数据串:0001 1100
多项式:
+
+
+ 1
得到
数据串(被除数):0001 1100 0000 0000
多项式(除数): 1 0000 0111
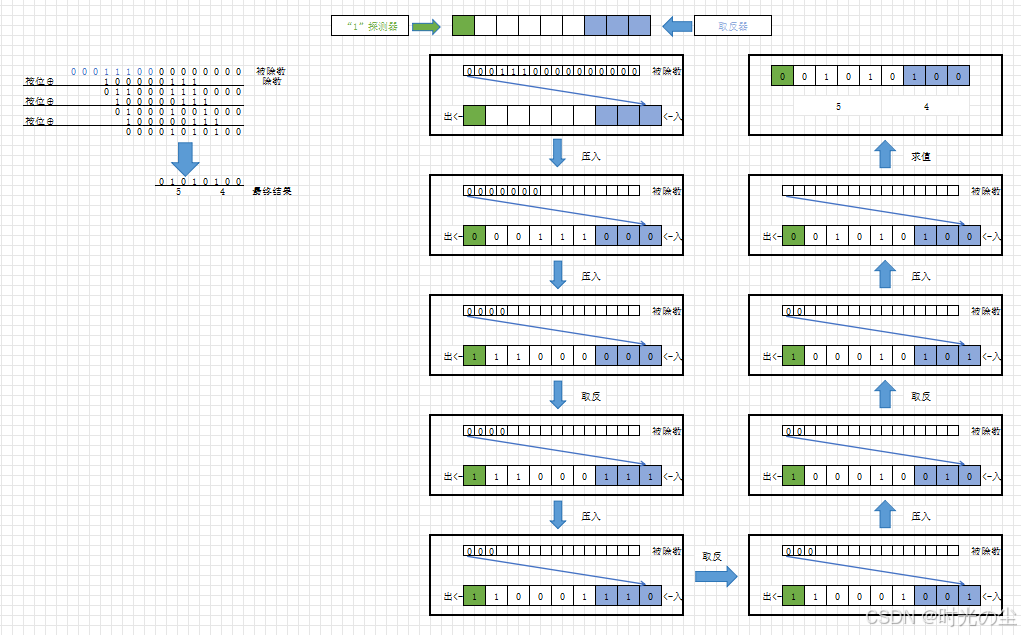
在开始编写代码前,我们先看一下CRC校验直观的运算过程,了解一下其原理,首先我们生成一个运算器:
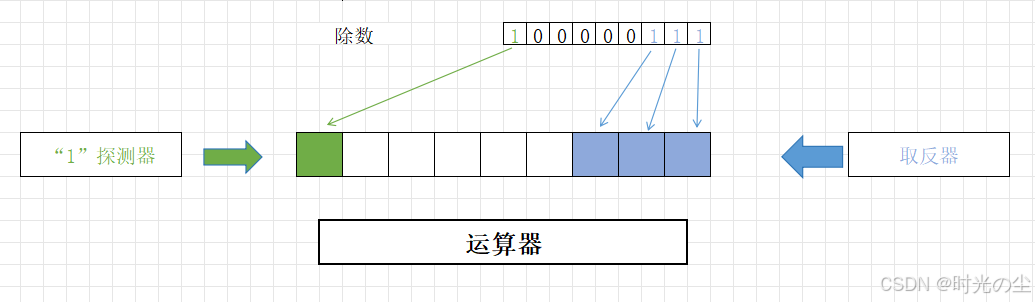
这样的运算器是怎么来的呢?我们看一下我们之前的运算过程,由于除数的最高位一定为1,并且除数的最高位在运算过程中,一定需要与被除数的最高有效位对齐,我们又知道根据异或操作,在二进制中无论0或者1,只要与1异或,可以理解为取反操作,因为0⊕1得1,1⊕1得0:
那么我们是不是可以认为每当最高位检测到1,那么除数中1对照的被除数,皆会进行取反操作:
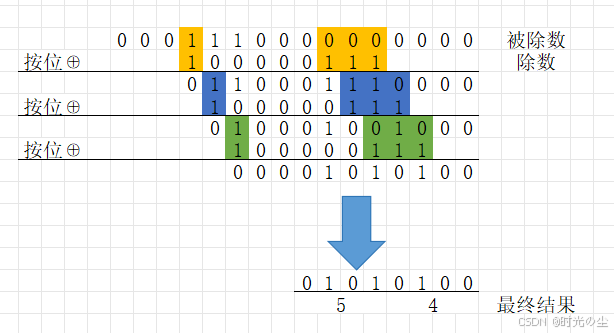
这样每当探测器检测到1,取反器就开始取反:

实际使用看看,将被除数依次通过入口放入到运算器当中:
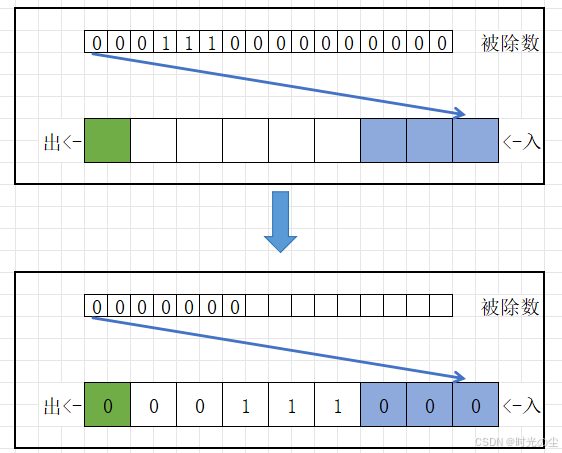
一直放入数据直到检测器检测到“1”:
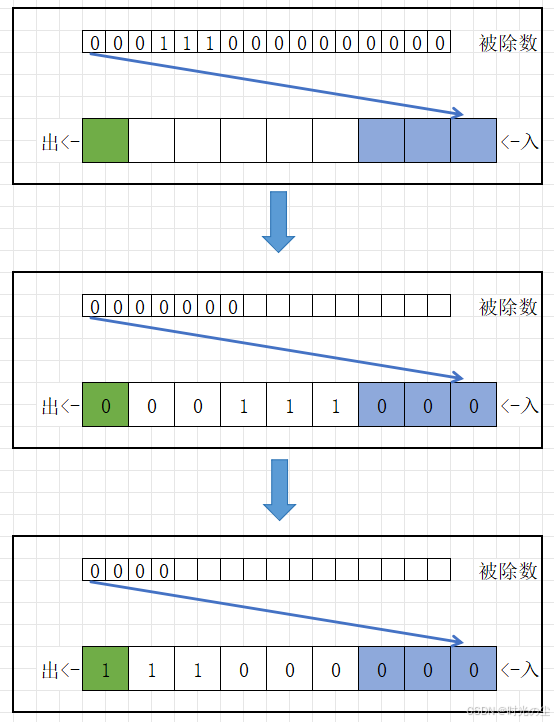
此时检测器启动取反器,将数据取反:
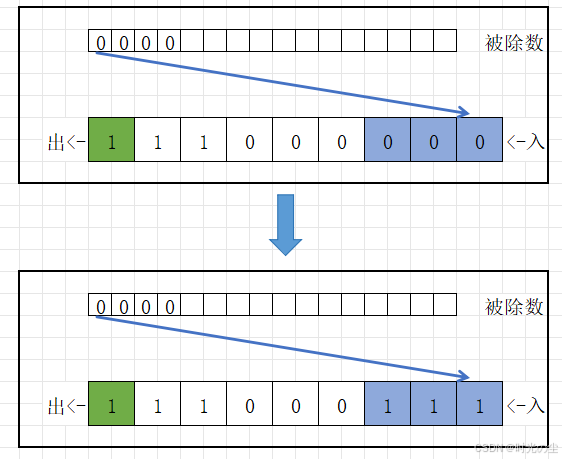
取反完后数据继续压入,直到再次检测到一,再次取反:
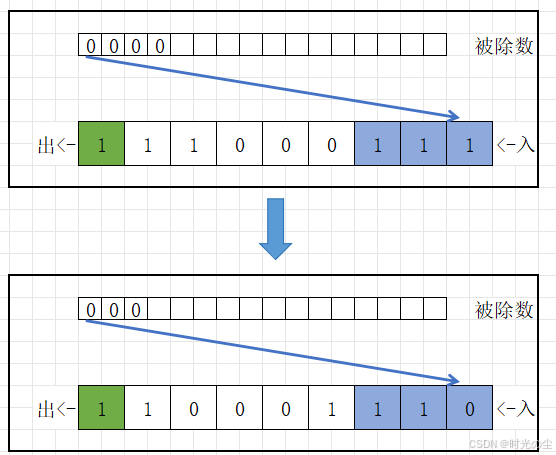
一直循环,直到所有数据压入完成,此时运算器剩余数据就是所得值,注意从低到高取最高次幂的位数,这里最高次幂为 ,因此取8位,所得值为0x54:
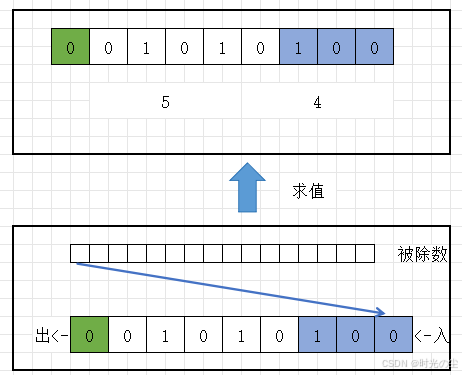
完整过程:
原理了解完了我们来开始着手编写代码,首先声明一下多项式,注意这里声明不包含检测器“1”,也就是我们正常多项式为0x107,但是我们最高位当做检测器,在CRC实际计算中被隐式声明了:
uint8_t poly = 0x07; // 多项式低8位(0x107去掉最高位)创建一个初始值用于存放每次移位后运算器的值:
uint8_t crc = 0x00; // 初始值检查CRC寄存器的最高位与当前数据位的异或结果,如果条件满足,左移CRC寄存器并与多项式进行异或,如果条件不满足,只需将CRC寄存器左移一位:
for (int i = 0; i < 8; i++)
{
uint8_t msb = (crc >> 7) & 0x01; // 取 crc 的最高位
crc <<= 1; // 左移 1 位
if (msb)
{ // 如果最高位是 1,才异或 poly
crc ^= poly;
}
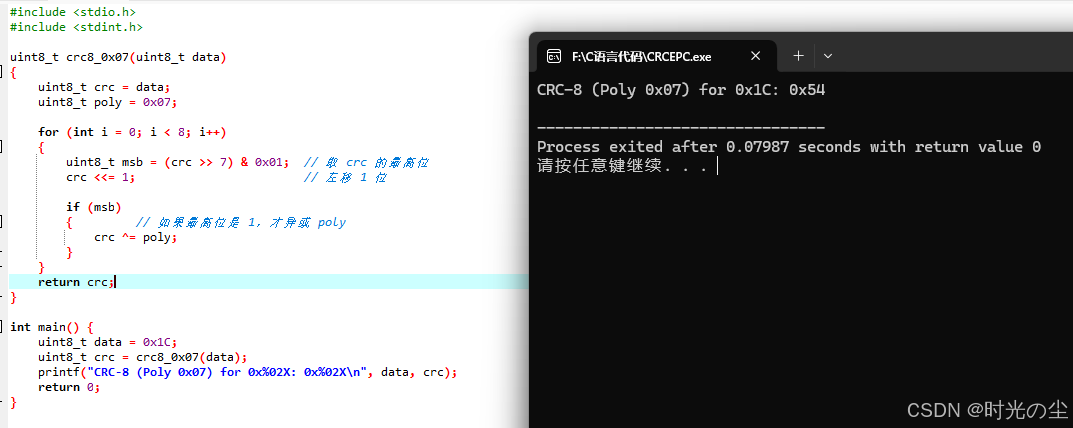
}完整代码:
#include <stdio.h>
#include <stdint.h>
uint8_t crc8_0x07(uint8_t data)
{
uint8_t crc = data;
uint8_t poly = 0x07;
for (int i = 0; i < 8; i++)
{
uint8_t msb = (crc >> 7) & 0x01; // 取 crc 的最高位
crc <<= 1; // 左移 1 位
if (msb)
{ // 如果最高位是 1,才异或 poly
crc ^= poly;
}
}
return crc;
}
int main() {
uint8_t data = 0x1C;
uint8_t crc = crc8_0x07(data);
printf("CRC-8 (Poly 0x07) for 0x%02X: 0x%02X\n", data, crc);
return 0;
}
5. 拓展:C语言代码编写二
上面我们编写了CRC-8的代码,但是在实际使用过程在,上述代码其实是不规范,首先,在我们上面给出的常见的CRC模型中,可以看出CRC的初始值是0x00,而我们上面代码并没有初始值这一项,除此之外,需要遵循MSB(最高有效位优先)的处理方式,我们直接去的全是我们运算器值的最高位,这样做也不能说错,但是对于实际使用更改其他模型不是很方便。
我们将代码更改一下,完整代码:
#include <stdio.h>
#include <stdint.h>
/**
* @brief 计算CRC-8(多项式0x107,MSB First)
* @param data 输入数据
* @return uint8_t CRC校验值
*/
uint8_t crc8_0x107(uint8_t data)
{
uint8_t crc = 0x00; // 初始值
uint8_t poly = 0x07; // 多项式低8位(0x107去掉最高位)
for (int i = 7; i >= 0; i--) // MSB First处理,循环从最高位(第7位)开始处理到最低位(第0位),实现MSB(最高有效位优先)的处理方式
{
uint8_t bit = (data >> i) & 0x01;//将数据右移i位后与0x01进行与操作,提取当前要处理的bit
if ((crc >> 7) ^ bit) //检查CRC寄存器的最高位与当前数据位的异或结果
{
crc = (crc << 1) ^ poly;
}
else
{
crc <<= 1;
}
}
return crc;
}
int main()
{
uint8_t data = 0x1C;
uint8_t crc = crc8_0x107(data);
printf("CRC-8 (Poly 0x107) for 0x%02X: 0x%02X\n", data, crc);
return 0;
}流程:
初始CRC: 00000000
处理第7位(0): CRC最高位0 ^ 0 = 0 → 左移 → 00000000
处理第6位(0): 同上 → 00000000
处理第5位(0): 同上 → 00000000
处理第4位(1): CRC最高位0 ^ 1 = 1 → (00000000 << 1) ^ 00000111 = 00000111
处理第3位(1): CRC最高位0 ^ 1 = 1 → (00000111 << 1) ^ 00000111 = 00001001
处理第2位(1): CRC最高位0 ^ 1 = 1 → (00001001 << 1) ^ 00000111 = 00010101
处理第1位(0): CRC最高位0 ^ 0 = 0 → 00010101 << 1 = 00101010
处理第0位(0): CRC最高位0 ^ 0 = 0 → 00101010 << 1 = 01010100
6. 拓展:C语言代码编写三
上面我们会发现,每次只能处理一个字节的数据在实际使用过程中还不是很方便,那么如果我们想要实现随机输入数组,进行处理要如何实现呢?
注意期间使用的函数,若是不理解的可以去下方链接查看,所提到的函数皆有涉及,这里只是简述其用法,不做详解,不然篇幅过长,还有点跑偏了,毕竟是讲CRC的:
首先对于随机输入,我们通过调用 fgets() 函数实现读取我们输入的数据,由于 fgets() 函数不能自己移出换行符,因此需要我们手动移调:
printf("请输入十六进制数据(用空格分隔,例如: 1C A3 45): ");
fgets(input, sizeof(input), stdin);
input[strcspn(input, "\n")] = '\0'; // 移除换行符对于输入的数据,我们通过字符串分割函数 strtok() 进行分割,存入到数组当中,为了避免修改原数据我们只对 strdup() 复制的数据进行修改,完成后注意讲修改完的内存空间清除:
int hex_string_to_bytes(const char *hex, uint8_t *bytes) {
int count = 0;
char *token;
char *copy = strdup(hex); // 复制字符串以避免修改原数据
token = strtok(copy, " "); // 按空格分割字符串
while (token != NULL) {
bytes[count++] = (uint8_t)strtol(token, NULL, 16); // 转换为字节
token = strtok(NULL, " ");
}
free(copy);
return count;
}对分割好的数据,我们逐字节进行CRC数据处理:
uint8_t crc8_stream(const uint8_t *data, size_t len) {
uint8_t crc = 0x00; // 初始值
for (size_t i = 0; i < len; i++) {
crc = crc8_update(crc, data[i]); // 逐字节更新CRC
}
return crc;
}CRC处理函数我们还是沿用上面的:
uint8_t crc8_update(uint8_t crc, uint8_t data) {
uint8_t poly = 0x07; // 多项式低8位(0x107去掉最高位)
for (int i = 7; i >= 0; i--) { // 从最高位开始处理
uint8_t bit = (data >> i) & 0x01;
if ((crc >> 7) ^ bit) {
crc = (crc << 1) ^ poly;
} else {
crc <<= 1;
}
}
return crc;
}
完整代码:
#include <stdio.h>
#include <stdint.h>
#include <string.h>
#include <stdlib.h>
/**
* @brief 计算单字节CRC-8(多项式0x107,MSB First)
* @param crc 当前CRC寄存器值
* @param data 输入数据字节
* @return uint8_t 更新后的CRC值
*/
uint8_t crc8_update(uint8_t crc, uint8_t data) {
uint8_t poly = 0x07; // 多项式低8位(0x107去掉最高位)
for (int i = 7; i >= 0; i--) { // 从最高位开始处理
uint8_t bit = (data >> i) & 0x01;
if ((crc >> 7) ^ bit) {
crc = (crc << 1) ^ poly;
} else {
crc <<= 1;
}
}
return crc;
}
/**
* @brief 计算数据流的CRC-8校验值
* @param data 输入数据数组
* @param len 数据长度(字节数)
* @return uint8_t CRC校验值
*/
uint8_t crc8_stream(const uint8_t *data, size_t len) {
uint8_t crc = 0x00; // 初始值
for (size_t i = 0; i < len; i++) {
crc = crc8_update(crc, data[i]); // 逐字节更新CRC
}
return crc;
}
/**
* @brief 将十六进制字符串转换为字节数组
* @param hex 输入的十六进制字符串(如"1C A3 45")
* @param bytes 输出字节数组
* @return int 转换的字节数,失败返回-1
*/
int hex_string_to_bytes(const char *hex, uint8_t *bytes) {
int count = 0;
char *token;
char *copy = strdup(hex); // 复制字符串以避免修改原数据
token = strtok(copy, " "); // 按空格分割字符串
while (token != NULL) {
bytes[count++] = (uint8_t)strtol(token, NULL, 16); // 转换为字节
token = strtok(NULL, " ");
}
free(copy);
return count;
}
int main() {
char input[256];
uint8_t data[128];
size_t len;
printf("请输入十六进制数据(用空格分隔,例如: 1C A3 45): ");
fgets(input, sizeof(input), stdin);
input[strcspn(input, "\n")] = '\0'; // 移除换行符
// 转换输入数据为字节数组
len = hex_string_to_bytes(input, data);
if (len <= 0) {
printf("输入格式错误!\n");
return 1;
}
// 计算CRC-8
uint8_t crc = crc8_stream(data, len);
// 打印输入数据和CRC结果
printf("输入数据: ");
for (size_t i = 0; i < len; i++) {
printf("%02X ", data[i]);
}
printf("\nCRC-8 (Poly 0x107): 0x%02X\n", crc);
return 0;
}我们先输入0x1C看看:
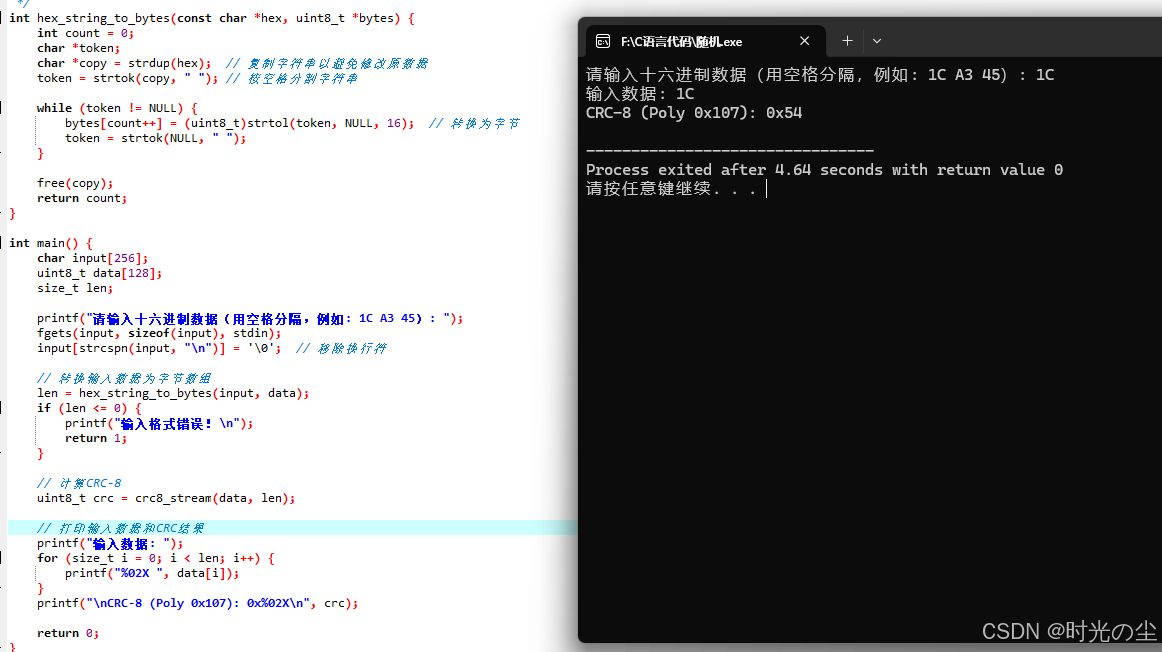
随便输一组数据:
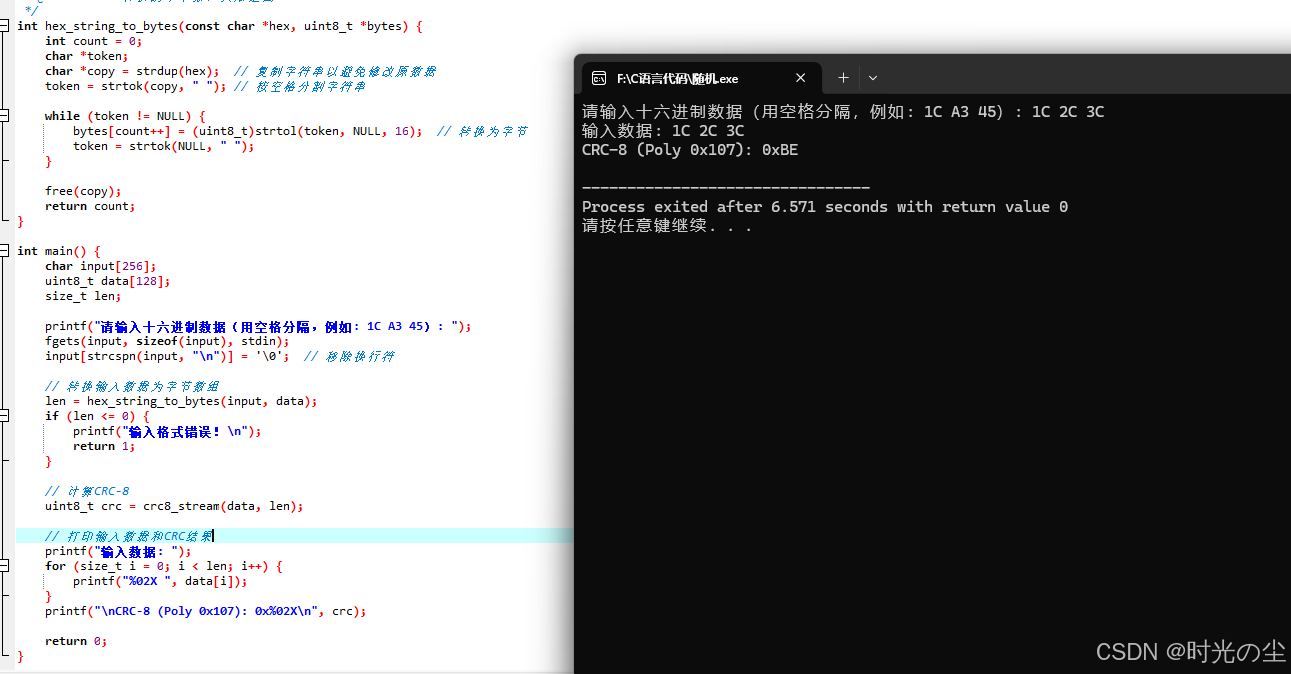
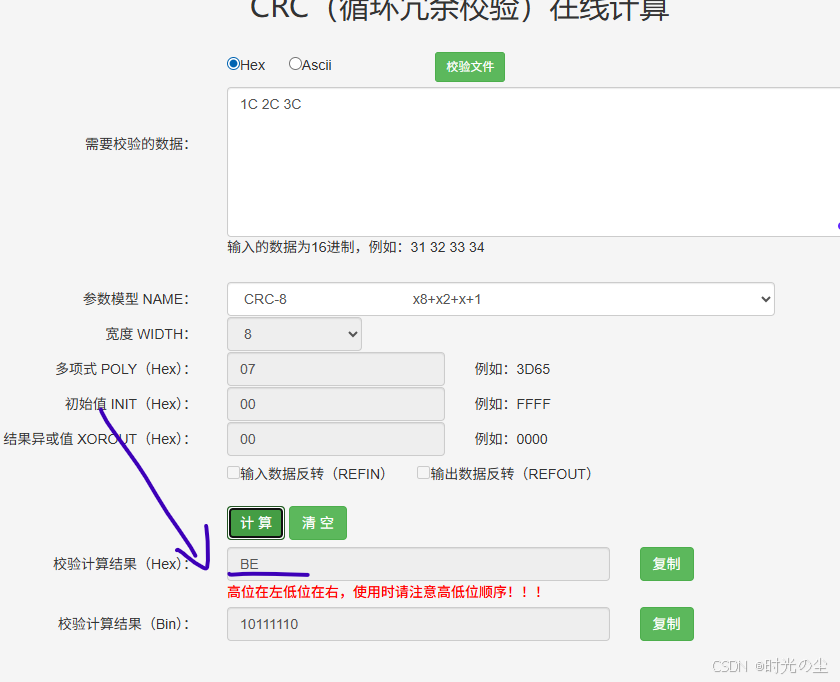
验证可行。
持续更新中,后续有新的需求会继续拓展,欢迎讨论


























 5290
5290












