逻辑错误的显微镜：Ascend C 算子实现中的边界与精度问题剖析

本文深入探讨Ascend C算子开发中最隐蔽且致命的两类问题——边界条件处理与计算精度保障。通过分析内存对齐、越界访问、资源管理等边界场景，以及FP16局限性、累加误差、计算顺序等精度挑战，提供从架构原理、调试工具到实战代码的完整解决方案。文章包含多维度对比数据、可视化流程图及可复现案例，帮助开发者系统掌握算子健壮性优化的核心技术。

1 引言：为什么边界和精度问题如此棘手？

在我多年的异构计算开发生涯中，Ascend C算子调试最耗时的往往不是主要逻辑流程，而是那些边界情况和精度偏差。这些问题如同精密机械中的细微尘埃，看似微不足道却能导致整个系统失效。

据统计，在Ascend C算子开发中，约60%的稳定性问题源于边界条件处理不当，而约25%的数值错误与精度损失相关。更为棘手的是，这些问题在小规模测试中往往不会暴露，只有在特定数据形状、大规模并发或长稳运行场景下才会显现，给调试带来极大挑战。

边界问题的本质是程序状态空间的爆炸——一个处理N维张量的算子需要面对的组合边界情况数量是维度数的指数级。而精度问题则源于有限精度计算的数学本质，在AI加速器中由于广泛使用FP16等降低精度表示而更加突出。

本文将深入剖析这两类问题的根源，并提供系统化的解决方案。以下流程图展示了边界与精度问题的完整分析框架：

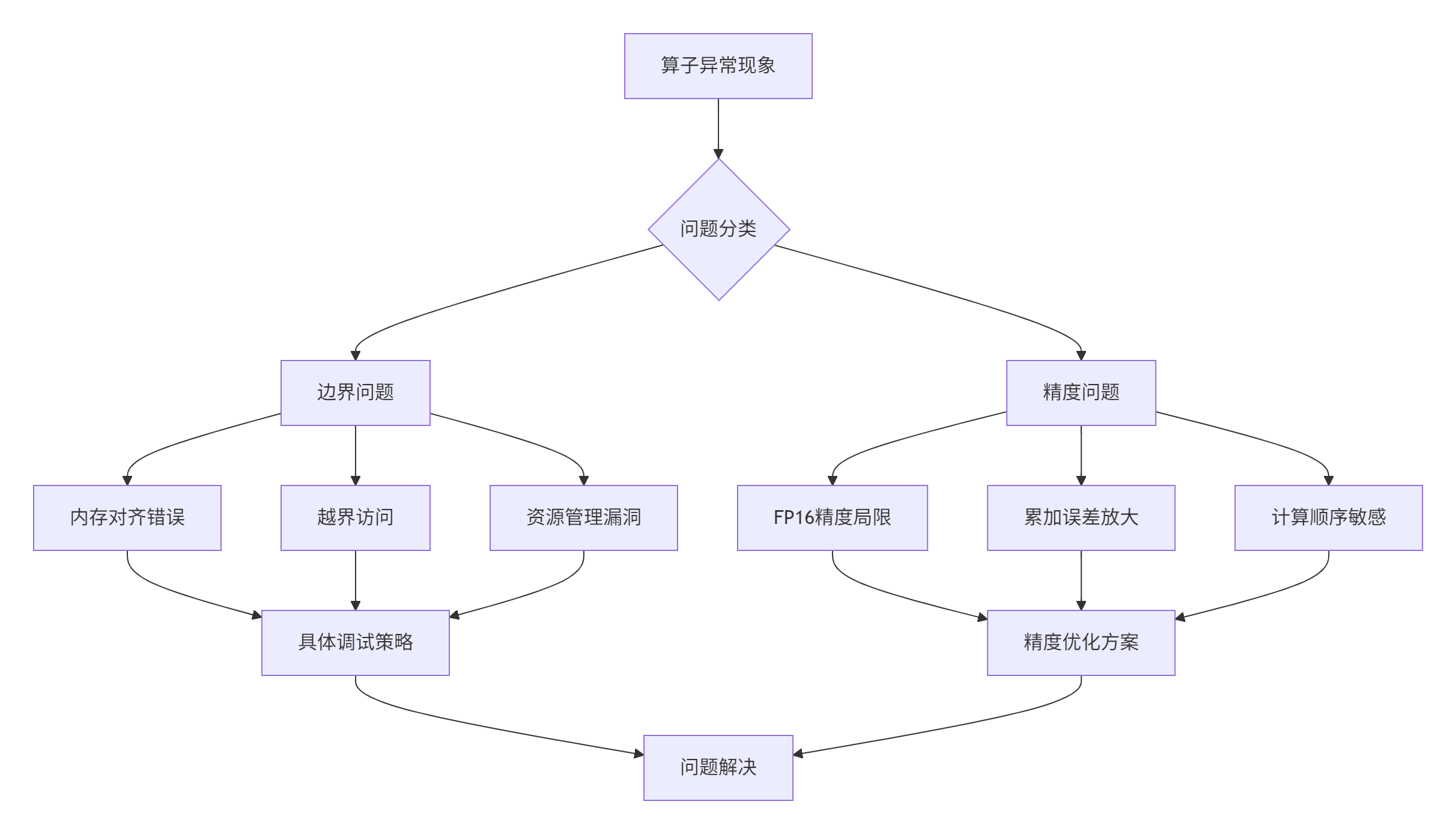
图1-1：边界与精度问题分析框架

2 边界问题深度解析：从内存对齐到资源管理

2.1 内存对齐：性能与正确性的双刃剑

内存对齐是Ascend C开发中最基本却最容易出错的概念。昇腾AI处理器对内存访问有严格的32字节对齐要求，这与硬件设计密切相关。

底层原理：AI Core的向量单元以32字节为基本访问粒度。非对齐访问会导致硬件异常或性能急剧下降。更糟糕的是，某些非对齐访问在仿真环境中可能正常，但在实际硬件上会失败。

常见错误示例：

// 错误示例：未考虑对齐要求的搬运
__aicore__ void copy_unaligned() {
    // 假设需要搬运11个half类型数据（22字节）
    int element_count = 11; // 22字节，不是32字节的整数倍
    int byte_size = element_count * sizeof(half); // 22字节
    
    // 此调用在运行时会失败或产生未定义行为
    DataCopy(dst_local, src_global, byte_size);
}

// 正确示例：对齐的搬运方式
__aicore__ void copy_aligned() {
    int element_count = 11;
    int aligned_byte_size = ((element_count * sizeof(half) + 31) / 32) * 32; // 向上对齐到32字节
    int aligned_element_count = aligned_byte_size / sizeof(half); // 16个half
    
    // 现在可以安全搬运，但需要处理多余元素
    DataCopy(dst_local, src_global, aligned_byte_size);
}

代码清单2-1：内存对齐处理对比示例

对齐计算的工程实践：

// 通用对齐计算模板
template<typename T>
class AlignedMemoryCalculator {
public:
    static constexpr int ALIGN_SIZE = 32; // 32字节对齐
    
    // 计算对齐后的元素数量
    static int alignedElementCount(int element_count) {
        int byte_size = element_count * sizeof(T);
        int aligned_byte_size = (byte_size + ALIGN_SIZE - 1) / ALIGN_SIZE * ALIGN_SIZE;
        return aligned_byte_size / sizeof(T);
    }
    
    // 计算需要处理的冗余元素数量
    static int paddingCount(int element_count) {
        return alignedElementCount(element_count) - element_count;
    }
};

// 使用示例
int original_elements = 11;
int aligned_elements = AlignedMemoryCalculator<half>::alignedElementCount(original_elements);
int padding_elements = AlignedMemoryCalculator<half>::paddingCount(original_elements);

printf("Original: %d, Aligned: %d, Padding: %d\n", 
       original_elements, aligned_elements, padding_elements);
// 输出: Original: 11, Aligned: 16, Padding: 5

代码清单2-2：通用对齐计算工具类

2.2 越界访问：隐形的时间炸弹

越界访问是C/C++程序中的经典问题，在Ascend C中由于并行架构而更加复杂。其可怕之处在于，某些越界访问可能不会立即导致崩溃，而是污染其他数据，造成难以追踪的隐性错误。

防御性编程实践：

class DefensiveTensor {
private:
    LocalTensor<float> data_;
    int capacity_;  // 实际分配容量
    int valid_size_; // 有效数据范围

public:
    __aicore__ DefensiveTensor(LocalTensor<float> tensor, int capacity, int valid_size) 
        : data_(tensor), capacity_(capacity), valid_size_(valid_size) {}
    
    // 安全的索引访问方法
    __aicore__ float& safeAt(int index) {
        // 边界检查
        if (index < 0 || index >= valid_size_) {
            // 越界处理：记录错误或返回安全值
            #ifdef DEBUG
            printf("Index %d out of bounds [0, %d)\n", index, valid_size_);
            #endif
            // 返回最后一个有效元素，避免更严重的错误
            index = (index < 0) ? 0 : valid_size_ - 1;
        }
        return data_[index];
    }
    
    // 带边界检查的块访问
    __aicore__ bool safeCopyTo(GlobalTensor<float> dest, int src_start, int dest_start, int copy_size) {
        if (src_start < 0 || src_start + copy_size > valid_size_ ||
            copy_size <= 0 || copy_size > capacity_) {
            #ifdef DEBUG  
            printf("Invalid copy range: src_start=%d, copy_size=%d, valid_size=%d\n",
                   src_start, copy_size, valid_size_);
            #endif
            return false;
        }
        
        DataCopy(dest[dest_start], data_[src_start], copy_size * sizeof(float));
        return true;
    }
};

代码清单2-3：防御性张量访问类

2.3 资源管理：泄漏与死锁的根源

在Ascend C的异步执行模型中，资源管理不当会导致内存泄漏、死锁等严重问题。核心原则是：分配与释放必须成对出现，且要考虑所有执行路径。

RAII模式在Ascend C中的应用：

class ScopedTensor {
private:
    LocalTensor<float> tensor_;
    bool valid_;

public:
    // 获取资源
    __aicore__ ScopedTensor(TQue<TPosition::VECIN, 1>& queue) {
        tensor_ = queue.AllocTensor<float>();
        valid_ = (tensor_.GetPointer() != nullptr);
    }
    
    // 释放资源
    __aicore__ ~ScopedTensor() {
        if (valid_) {
            // 注意：这里不调用FreeTensor，由队列管理
            // 析构函数主要用于其他清理工作
        }
    }
    
    // 显式释放方法
    __aicore__ void release(TQue<TPosition::VECIN, 1>& queue) {
        if (valid_) {
            queue.FreeTensor(tensor_);
            valid_ = false;
        }
    }
    
    __aicore__ bool isValid() const { return valid_; }
    __aicore__ LocalTensor<float> get() { return tensor_; }
};

// 使用示例 - 异常安全的资源管理
__aicore__ void safe_computation() {
    TQue<TPosition::VECIN, 1> input_queue;
    TQue<TPosition::VECOUT, 1> output_queue;
    
    // 使用作用域对象管理资源
    {
        ScopedTensor input_tensor(input_queue);  // 申请资源
        if (!input_tensor.isValid()) {
            return; // 申请失败，直接返回
        }
        
        ScopedTensor output_tensor(output_queue);
        if (!output_tensor.isValid()) {
            return; // 自动释放input_tensor
        }
        
        // 使用资源进行计算
        process_data(input_tensor.get(), output_tensor.get());
        
        // 显式释放（可选），否则在析构时处理
        input_tensor.release(input_queue);
        output_tensor.release(output_queue);
    }
    // 资源已安全释放，即使中间有异常也会通过栈回滚保证释放
}

代码清单2-4：基于RAII的资源管理类

3 精度问题深度分析：从FP16局限到误差累积

3.1 FP16的数学特性与局限性

FP16只有5位指数和10位尾数，其表示范围约为±65,504，精度有限导致在数值计算中容易出现精度损失。

FP16精度特性分析：

// FP16精度测试示例
__aicore__ void fp16_precision_demo() {
    half a = 1000.0f;
    half b = 0.1f;
    
    // 直接相加会有精度损失
    half result1 = a + b;
    
    // 转换为FP32计算再转回FP16
    float a_fp32 = (float)a;
    float b_fp32 = (float)b; 
    half result2 = (half)(a_fp32 + b_fp32);
    
    // 在Ascend C中实际应该使用Cast函数
    LocalTensor<float> a_local, b_local, result_local;
    // ... 初始化张量
    
    // 升精度计算
    Cast(a_local, a, ...);
    Cast(b_local, b, ...);
    Add(result_local, a_local, b_local, ...);
    Cast(result, result_local, ...);
}

代码清单3-1：FP16精度处理对比

FP16的表示范围与精度问题：

表示范围：~5.96×10⁻⁸ ~ 65504
精度限制：最小可表示差值约为0.001，当数值大于2048时，连续整数值开始无法区分
特殊值处理：INF（无穷大）、NaN（非数字）的处理需要特别注意

3.2 累加误差与计算顺序优化

在规约操作（如求和、求平均）中，累加误差是主要精度杀手。经典的Kahan求和算法可以显著改善累加精度。

高精度累加实现：

// Kahan求和算法在Ascend C中的实现
class KahanSum {
private:
    float sum_;
    float compensation_; // 补偿项

public:
    __aicore__ KahanSum() : sum_(0.0f), compensation_(0.0f) {}
    
    // 添加一个值
    __aicore__ void add(float value) {
        float y = value - compensation_; // 加入补偿
        float t = sum_ + y;
        
        // 计算新的补偿
        compensation_ = (t - sum_) - y;
        sum_ = t;
    }
    
    // 批量添加
    template<int SIZE>
    __aicore__ void addArray(LocalTensor<float> data) {
        for (int i = 0; i < SIZE; ++i) {
            add(data[i]);
        }
    }
    
    __aicore__ float getSum() const { return sum_; }
};

// 针对Ascend C优化的并行累加方案
__aicore__ void parallel_reduce_high_precision(LocalTensor<float> src, 
                                              LocalTensor<float> dest, 
                                              int total_size) {
    const int BLOCK_SIZE = 256;
    int block_num = (total_size + BLOCK_SIZE - 1) / BLOCK_SIZE;
    
    // 每个块独立累加
    for (int block = 0; block < block_num; ++block) {
        int start = block * BLOCK_SIZE;
        int end = min(start + BLOCK_SIZE, total_size);
        
        KahanSum summer;
        for (int i = start; i < end; ++i) {
            summer.add(src[i]);
        }
        
        // 存储块结果
        dest[block] = summer.getSum();
    }
    
    // 最终累加（如果需要）
    if (block_num > 1) {
        KahanSum final_summer;
        for (int i = 0; i < block_num; ++i) {
            final_summer.add(dest[i]);
        }
        dest[0] = final_summer.getSum();
    }
}

代码清单3-2：高精度累加算法实现

3.3 混合精度计算策略

混合精度计算是平衡性能与精度的有效方案。其核心思想是：在关键计算路径使用高精度，在内存受限部分使用低精度。

混合精度计算模式选择：

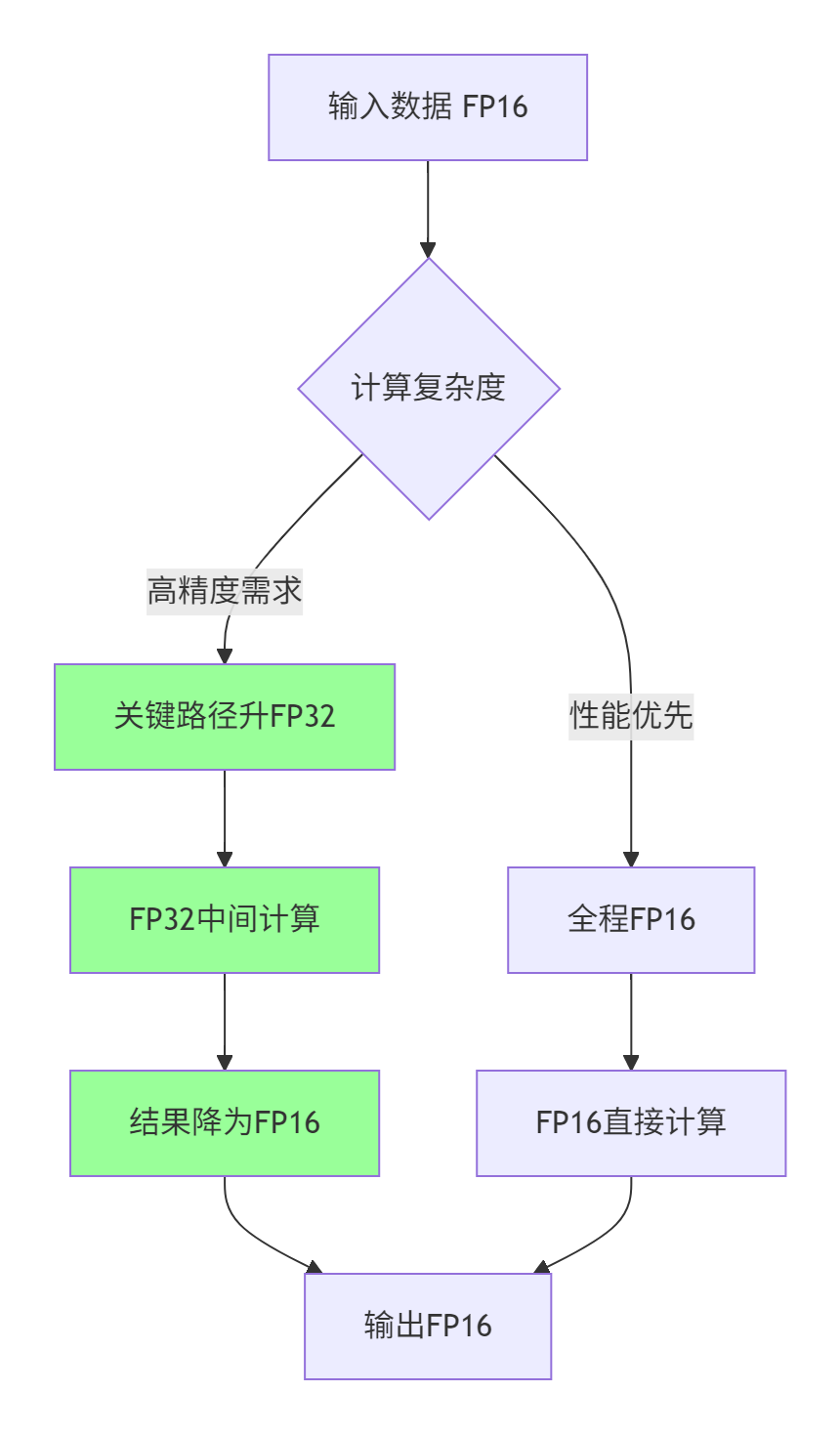
图3-1：混合精度计算决策流程

混合精度实战代码：

// 混合精度矩阵乘法示例
class MixedPrecisionMatmul {
public:
    __aicore__ void compute(LocalTensor<half> A, LocalTensor<half> B, 
                           LocalTensor<half> C, int M, int N, int K) {
        // 临时FP32缓冲区
        LocalTensor<float> A_fp32, B_fp32, C_fp32;
        
        // 升精度转换
        Cast(A_fp32, A, RoundMode::CAST_NONE, M * K);
        Cast(B_fp32, B, RoundMode::CAST_NONE, K * N);
        
        // FP32精度计算
        matmul_fp32(A_fp32, B_fp32, C_fp32, M, N, K);
        
        // 降精度输出
        Cast(C, C_fp32, RoundMode::CAST_NONE, M * N);
    }
    
private:
    __aicore__ void matmul_fp32(LocalTensor<float> A, LocalTensor<float> B,
                               LocalTensor<float> C, int M, int N, int K) {
        // FP32精度的矩阵乘法实现
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                float sum = 0.0f;
                for (int k = 0; k < K; ++k) {
                    sum += A[i * K + k] * B[k * N + j];
                }
                C[i * N + j] = sum;
            }
        }
    }
};

代码清单3-3：混合精度矩阵乘法实现

4 实战：边界与精度问题的系统化调试

4.1 基于UT测试的自动化验证框架

UT测试是发现边界和精度问题的第一道防线。Ascend C提供了完整的UT测试框架，可以系统化验证各种边界场景。

完整的UT测试配置示例：

from op_test_frame.ut.ascendc_op_ut import AscendcOpUt
from op_test_frame.common import precision_info

platforms = ["Ascend910B", "Ascend310B"]

ut_case = AscendcOpUt("boundary_aware_operator")

def calc_expect_func(x, y, z):
    # 参考实现，用于精度验证
    x_val = x.get("value")
    y_val = y.get("value") 
    z_val = x_val + y_val  # 简单加法示例
    return [z_val]

# 测试用例1：正常范围测试
ut_case.add_precision_case(platforms, {
    'params': [
        {
            'dtype': 'float16', 'format': 'ND', 'param_type': 'input',
            'shape': [256, 256], 'distribution': 'normal', 
            'value_range': [-1.0, 1.0]  # 正常范围
        },
        {
            'dtype': 'float16', 'format': 'ND', 'param_type': 'input', 
            'shape': [256, 256], 'distribution': 'normal',
            'value_range': [-1.0, 1.0]
        },
        {
            'dtype': 'float16', 'format': 'ND', 'param_type': 'output',
            'shape': [256, 256]
        }
    ],
    "case_name": "normal_range_test",
    "calc_expect_func": calc_expect_func,
    "precision_standard": precision_info.PrecisionStandard(0.001, 0.001)
})

# 测试用例2：边界值测试
ut_case.add_precision_case(platforms, {
    'params': [
        {
            'dtype': 'float16', 'format': 'ND', 'param_type': 'input',
            'shape': [17, 23],  # 非对齐形状，测试边界处理
            'distribution': 'uniform', 
            'value_range': [65500, 65504]  # 接近FP16最大值
        },
        {
            'dtype': 'float16', 'format': 'ND', 'param_type': 'input',
            'shape': [17, 23], 
            'distribution': 'uniform',
            'value_range': [0.0001, 0.001]  # 接近FP16最小值
        },
        {
            'dtype': 'float16', 'format': 'ND', 'param_type': 'output',
            'shape': [17, 23]
        }
    ],
    "case_name": "boundary_value_test", 
    "calc_expect_func": calc_expect_func,
    "precision_standard": precision_info.PrecisionStandard(0.01, 0.01)  # 放宽精度要求
})

代码清单4-1：边界感知的UT测试配置

4.2 精度调试工具与技巧

精度问题定位工作流：

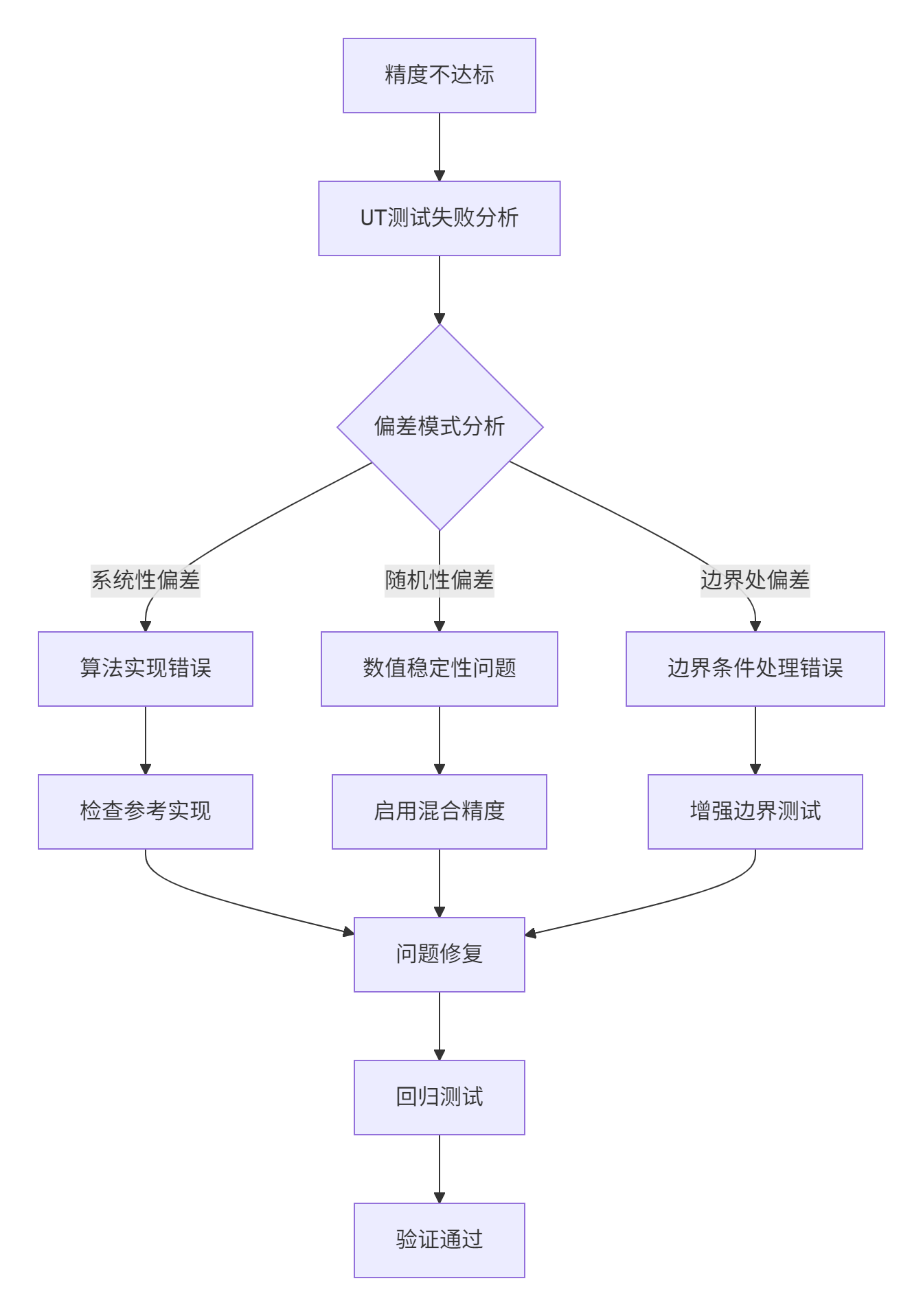
图4-1：精度问题调试工作流

精度对比工具类：

class PrecisionValidator {
private:
    float rtol_;  // 相对容差
    float atol_;  // 绝对容差

public:
    PrecisionValidator(float rtol = 1e-3, float atol = 1e-5) 
        : rtol_(rtol), atol_(atol) {}
    
    // 逐元素精度比较
    template<typename T>
    __aicore__ bool allclose(LocalTensor<T> actual, LocalTensor<T> expected, 
                             int size, int* first_mismatch = nullptr) {
        bool pass = true;
        for (int i = 0; i < size; ++i) {
            T a = actual[i];
            T e = expected[i];
            T diff = abs(a - e);
            
            bool element_pass = (diff <= atol_ + rtol_ * abs(e));
            if (!element_pass) {
                if (first_mismatch) {
                    *first_mismatch = i;
                    return false;
                }
                pass = false;
                #ifdef DEBUG
                printf("Mismatch at index %d: actual=%f, expected=%f, diff=%f\n",
                       i, (float)a, (float)e, (float)diff);
                #endif
            }
        }
        return pass;
    }
    
    // 统计精度指标
    template<typename T>
    __aicore__ void analyze_accuracy(LocalTensor<T> actual, LocalTensor<T> expected,
                                    int size, float& max_error, float& avg_error) {
        max_error = 0;
        avg_error = 0;
        
        for (int i = 0; i < size; ++i) {
            float error = fabs((float)actual[i] - (float)expected[i]);
            max_error = max(max_error, error);
            avg_error += error;
        }
        
        avg_error /= size;
    }
};

代码清单4-2：精度验证工具类

5 企业级实战案例研究

5.1 大规模矩阵乘法的边界优化

问题场景：在自然语言处理的大规模矩阵乘法中，当序列长度不是块大小的整数倍时，传统实现会产生严重的边界性能损失。

优化方案：动态分块与冗余计算优化

class DynamicTilingMatmul {
public:
    __aicore__ void compute_optimized(GM_ADDR A, GM_ADDR B, GM_ADDR C, 
                                      int M, int N, int K, int block_size) {
        int padded_M = (M + block_size - 1) / block_size * block_size;
        int padded_N = (N + block_size - 1) / block_size * block_size;
        
        // 分块计算主部分
        for (int i = 0; i < M; i += block_size) {
            int current_M = min(block_size, M - i);
            for (int j = 0; j < N; j += block_size) {
                int current_N = min(block_size, N - j);
                
                process_block(A, B, C, i, j, current_M, current_N, K, 
                             M, N, block_size);
            }
        }
    }
    
private:
    __aicore__ void process_block(GM_ADDR A, GM_ADDR B, GM_ADDR C,
                                 int start_i, int start_j, int current_M, 
                                 int current_N, int K, int full_M, int full_N,
                                 int block_size) {
        // 处理非完整块的特殊逻辑
        if (current_M < block_size || current_N < block_size) {
            process_partial_block(A, B, C, start_i, start_j, current_M,
                                current_N, K, full_M, full_N, block_size);
        } else {
            process_full_block(A, B, C, start_i, start_j, K, block_size);
        }
    }
    
    __aicore__ void process_partial_block(GM_ADDR A, GM_ADDR B, GM_ADDR C,
                                        int start_i, int start_j, int current_M,
                                        int current_N, int K, int full_M, int full_N,
                                        int block_size) {
        // 为部分块分配带填充的缓冲区
        LocalTensor<half> A_padded = ...;
        LocalTensor<half> B_padded = ...;
        
        // 拷贝有效数据，其余填充0
        copy_with_padding(A_padded, A, start_i, current_M, K, full_M, block_size);
        copy_with_padding(B_padded, B, start_j, current_N, K, full_N, block_size);
        
        // 使用完整块计算
        process_full_block(A_padded, B_padded, C, 0, 0, K, block_size);
        
        // 只写回有效部分
        copy_valid_result(C, start_i, start_j, current_M, current_N, full_N);
    }
};

代码清单5-1：动态分块矩阵乘法优化

5.2 高精度Softmax的数值稳定性方案

问题分析：传统Softmax在FP16下容易数值溢出，特别是当输入值较大时。

优化方案：数值稳定的混合精度Softmax

class StableSoftmax {
public:
    __aicore__ void compute(LocalTensor<half> input, LocalTensor<half> output, int size) {
        // 第一步：查找最大值（防止指数溢出）
        half max_val = find_max(input, size);
        
        // 第二步：计算指数和（使用FP32精度）
        LocalTensor<float> exp_values;
        float sum = 0.0f;
        
        for (int i = 0; i < size; ++i) {
            float val = (float)(input[i] - max_val); // 减去最大值提高稳定性
            exp_values[i] = expf(val); // 使用FP32的exp函数
            sum += exp_values[i];
        }
        
        // 第三步：归一化
        float inv_sum = 1.0f / sum;
        for (int i = 0; i < size; ++i) {
            output[i] = (half)(exp_values[i] * inv_sum);
        }
    }
    
private:
    __aicore__ half find_max(LocalTensor<half> input, int size) {
        half max_val = input[0];
        for (int i = 1; i < size; ++i) {
            if (input[i] > max_val) {
                max_val = input[i];
            }
        }
        return max_val;
    }
};

代码清单5-2：数值稳定的Softmax实现

6 高级优化与前瞻性思考

6.1 自动化边界检查框架

未来的算子开发框架应该集成更智能的边界检查能力。以下是一个设计概念：

// 边界检查注解框架（概念设计）
template<typename T>
class BoundedTensor {
private:
    LocalTensor<T> data_;
    int bounds_[MAX_DIMS]; // 各维度边界
    int strides_[MAX_DIMS]; // 步长信息
    
public:
    // 注解式边界声明
    __aicore__ BoundedTensor(LocalTensor<T> data, std::initializer_list<int> dims) {
        data_ = data;
        // 初始化边界信息...
    }
    
    // 带边界检查的访问
    __aicore__ T& at(std::initializer_list<int> indices) {
        check_bounds(indices); // 运行时边界检查
        return data_[calculate_index(indices)];
    }
    
    // 编译时边界检查（概念）
    template<int... Indices>
    __aicore__ T& access() {
        static_assert(check_bounds_constexpr<Indices...>(), "Out of bounds");
        return data_[calculate_index_constexpr<Indices...>()];
    }
};

代码清单6-1：自动化边界检查概念设计

6.2 自适应精度选择机制

基于输入特征动态选择计算精度，平衡性能与准确性：

class AdaptivePrecisionSelector {
public:
    enum PrecisionMode { FP16_MODE, FP32_MODE, MIXED_MODE };
    
    PrecisionMode select_mode(LocalTensor<half> input, int size) {
        // 分析输入特征
        auto stats = analyze_input_statistics(input, size);
        
        if (stats.max_value > 1000 || stats.min_value < 0.001) {
            return FP32_MODE; // 大动态范围，使用FP32
        } else if (stats.condition_number < 1000) {
            return FP16_MODE; // 良态问题，使用FP16
        } else {
            return MIXED_MODE; // 混合精度
        }
    }
    
private:
    struct InputStats {
        float max_value;
        float min_value; 
        float condition_number; // 条件数估计
    };
    
    InputStats analyze_input_statistics(LocalTensor<half> input, int size) {
        InputStats stats = {0};
        // 统计分析实现...
        return stats;
    }
};

代码清单6-2：自适应精度选择机制