机器学习2：逻辑回归

逻辑回归 (Logistic Regression)

1）假设表示

逻辑回归模型的假设是：$h_{\theta }(x)=g({\theta }^{T}X)$，它的输出值永远在0到 1 之间。
其中：
X代表特征向量
g代表逻辑函数（logistic function)是一个常用的逻辑函数为S形函数（Sigmoid function），公式为：$g(z)=\frac{1}{1+e^{-z}}$ 。
$h_{\theta }(x)$的作用是，对于给定的输入变量，根据选择的参数计算其输出为1的可能性→$h_{\theta }(z)=P(y=1|x;\theta$）

Python代码实现：
import numpy as np
def sigmoid(z):
	return 1/(1+np.exp(-z))

sigmoid函数图像

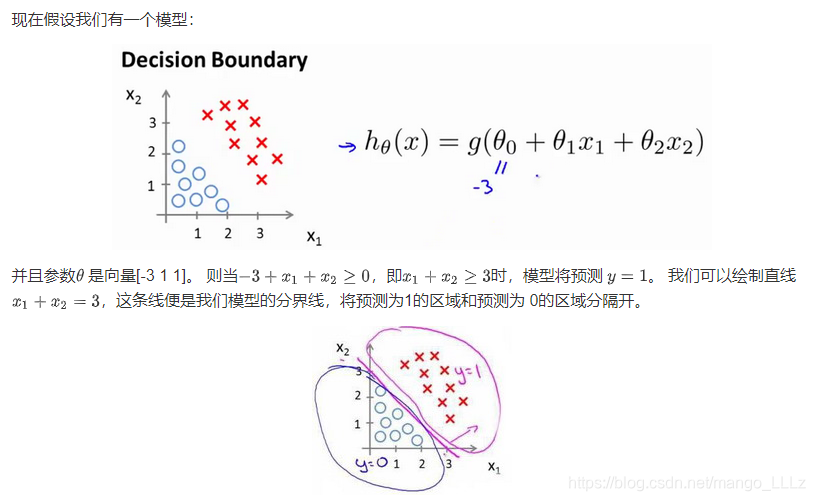
2）决策边界

在逻辑回归中有：
当 $h_{\theta }(x)>=0.5$ 时，预测 $y=1$；当 $h_{\theta }(x)<0.5$ 时，预测 $y=0$

由 $g(z)=\frac{1}{1+e^{-z}}$ 有：
$z>0$ 时，$g(z)>0.5$；$z=0$ 时，$g(z)=0.5$；$z<0$ 时，$g(z)<0.5$

又因为$z={\theta }^{T}x$，所以有：
${\theta }^{T}x>=0，y=1$；${\theta }^{T}x<0，y=0$

3）代价函数

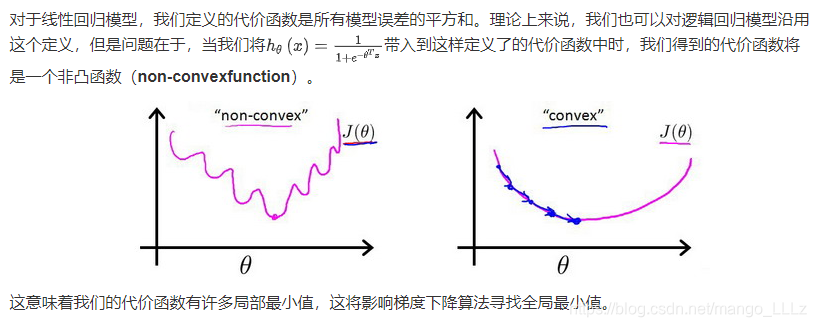
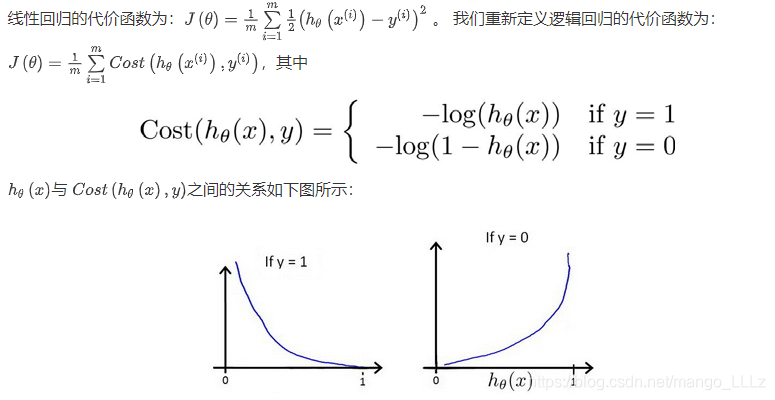
Cost函数简化如下：
$Cost(h_{\theta }(x),y)=-ylog(h_{\theta }(x))-(1-y)log(1-h_{\theta }(x))$

代入代价函数得：
$J(\theta )=\frac{1}{m}{\sum }_{i=1}^n[-y^{(i)}log(h_{\theta }(x^{(i)}))-(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$

Python代码实现：
import numpy as np
def cost(theta,X,y):
	theta = np.matrix(theta)
	X = np.matrix(X)
	y = np.matrix(y)
	m = len(X)
	h = sigmoid(X*theta.T)
	# np.multiply 矩阵对应元素位置相乘
	J = np.sum(np.multiply(-y,np.log(h))-np.multiply(1-y,np.log(1-h))) / m
	return J

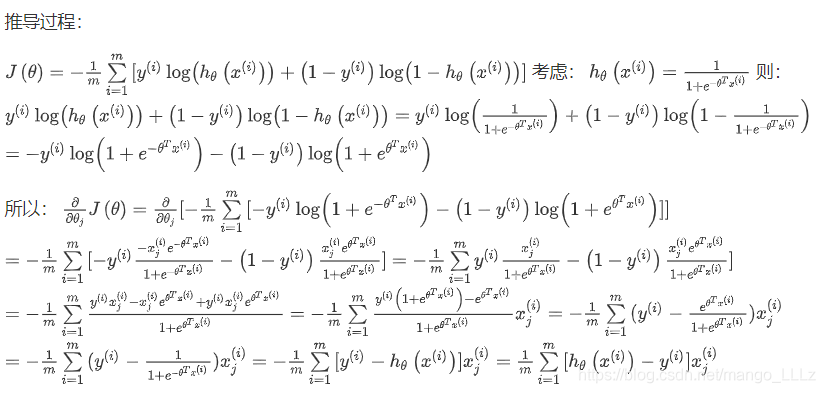
除了梯度下降算法以外，还有一些常被用来令代价函数最小的算法，这些算法更加复杂和优越，而且通常不需要人工选择学习率，通常比梯度下降算法要更加快速。这些算法有：共轭梯度（Conjugate Gradient），局部优化法(Broyden fletcher goldfarb shann,BFGS) 和 有限内存局部优化法(LBFGS)

4）正则化

给代价函数增加一个正则化的表达式，得到代价函数：
$J(\theta )=\frac{1}{m}{\sum }_{i=1}^m[-y^{(i)}log(h_{\theta }(x^{(i)}))-(1-y^{(i)})og(1-h_{\theta }(x^{(i)})log(1-h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}{\sum }_{j=1}^n{\theta }_j^2$
注意：${\theta }_0$不正则化

通过梯度下降算法求导，得出梯度为：
${\theta }_0:={\theta }_0-a\frac{1}{m}\sum _{i=1}^m((h_{\theta }(x^{(i)})-y^{(i)})x_0^{(i)})$

${\theta }_j:={\theta }_j-a[\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{\left(i\right)}+\frac{\lambda }{m}{\theta }_j]$