95. 不同的二叉搜索树 II

95. 不同的二叉搜索树 II

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例 1：

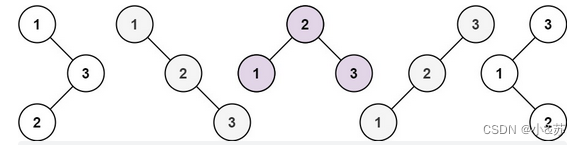
输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

1 <= n <= 8

思路：

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。

我们采用回溯算法来解题。
首先我们将起始位置和终止位置传入函数，如果起始大于结束位置的话，返回空指针。
开辟一个数组用来存储所有可行的二叉搜素树。
枚举可行根结点，我们设根结点为i，根结点左侧获取可行的左子树集合，start~i-1；根结点右侧获取可行的右子树集合，i+1 ~end。
从左子树集合中选出一棵左子树，从右子树集合中选出一棵右子树，拼接到根结点上。

主函数
如果n为0的话，返回空；
否则返回二叉搜素树的结果。

代码样例：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> generateTrees(int start,int end){
        if(start>end)
            return{nullptr};
        vector<TreeNode*> allTrees;
        for(int i=start;i<=end;i++){
            vector<TreeNode*> leftTrees=generateTrees(start,i-1);
            vector<TreeNode*> rightTrees=generateTrees(i+1,end);
            for(auto &left:leftTrees){
                for(auto &right:rightTrees){
                    TreeNode* currTree=new TreeNode(i);
                    currTree->left=left;
                    currTree->right=right;
                    allTrees.emplace_back(currTree);
                }
            }
        }
        return allTrees;
    }
    
    vector<TreeNode*> generateTrees(int n) {
        if(!n){
            return{};
        }
        return generateTrees(1,n);
    }
};